1

Испытания и события. Выше событие названо случайным, если при осуществлении определенной совокупности условий S оно может либо произойти, либо не произойти. В дальнейшем, вместо того чтобы говорить «совокупность условий S осуществлена», будем говорить кратко: «произведено испытание». Таким образом, событие будет рассматриваться как результат испытания.

примеры испытаний и событий

Виды случайных событий. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

2

Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.

Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них красные, 3-синие и 1-белый. Очевидно, возможность вынуть наудачу из урны цветной (т.е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появление цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.

ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Итак, вероятность события А определяется формулой:

 (1)

где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.

Пример 1 Найти вероятность события А={появление не менее пяти очков при одном бросании игральной кости}.

Используем формулу (1). В нашем случае число возможных исходов n=6, а число, благоприятствующих этому событию исходов, m=2. То есть P(A)=2/6=1/3. Итак, вероятность появления не менее пяти очков при одном бросании игральной кости равна 0.33 или 1/3

Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1

Свойство 2. Вероятность невозможного события равна нулю.

В этом случае m=0, следовательно, P(A)=m/n=0/n=0

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно,

0<P(A)<1

Итак, вероятность любого события удовлетворяет двойному неравенству

0 P(A) 1

3

Геометрическая вероятность — один из способов задания вероятности; пусть Ω — ограниченное множество евклидова пространства, имеющее объем λ(Ω) (соответственно длину или площадь в одномерной или двумерной ситуации), пусть ω — точка, взятая случайным образом из Ω, пусть вероятность, что точка будет взята из подмножества   пропорциональна его объёму λ(x), тогда геометрическая вероятность подмножества  определяется как отношение объёмов:

Геометрическое определение вероятности часто используется в методах Монте-Карло, например, для приближённого вычисления значений многократных определённых интегралов.

4

Теорема сложения вероятностей формулируется следующим образом.

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

.

По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.

[править]Определение

Пусть   есть вероятностное пространство. Любое разбиение множества   элементами сигма-алгебры   называется полной группой событий.

Противоположные события. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать

5

Произведение событий. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС — выпадение «герба» во всех трех испытаниях.

Условная вероятность. Во введении случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S.

Условной вероятностью Р_A (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

пример условной вероятности

Исходя из классического определения вероятности, формулуР_A (В) = Р (АВ) / Р (А) (Р (А) > 0 можно доказать. Это обстоятельство и служит основанием для следующего общего (применимого не только для классической вероятности) определения.

Условная вероятность события В при условии, что событие А уже наступило, по определению, равна

Р_A (В) = Р (АВ) / Р (А)    (Р(A)>0).

6

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

7

В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если значение одной из них не влияет на вероятность значений другой.

Теорема умножения для независимых событий

Теорема. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей: 

P(AB) = P(A)*P(B).

(2.5)

8

(формула полной вероятности). Пусть   — полная группа событий. Тогда вероятность любого события   может быть вычислена по формуле:

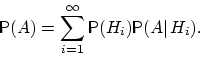
9

ФОРМУЛА ВЕРОЯТНОСТЕЙ ГИПОТЕЗ (ФОРМУЛА БАЙЕСА) —

формула, имеющая вид: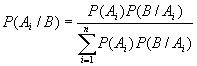 

где a₁, А₂,..., А_п — несовместимые события,  Общая схема применения Ф. в. г.: если событие В может происходить в разл. условиях, относительно которых сделано п гипотез А₁, А₂, ..., А_n с известными до опыта вероятностями P(A₁), P(A₂), ..., Р(А_n) и известны условные вероятности P(B/A_i), то после опыта, где наступило событие В. происходит переоценка вероятностей гипотез (в силу чего эту формулу называют Ф. в. г.). Формула Байеса может быть использована для оценки перспективности территорий, оценки палеогеографических реконструкций, направления разведки и т. п.

10

Повторные испытания. Формула Бернулли. Биномиальное распределение. Локальная и интегральная формулы Муавра-Лапласа

 

Схема испытаний Бернулли, биномиальное распределение.

Рассм серию повторных испытаний. Пусть результат каждого испытания есть появление одного из 2-х альтерн исходов. Наступление некот события A или противополож ему событию  . Испыт могут проводится:

1.  когда результат каждого испыт не зависит от предшеств испыт (такие испыт назыв независим)

2.  результат испыт зависит от рез-ов предыд испыт (зависимые испыт)

Независим испыт в свою очередь могут произв в одинаковых или различных условиях. В первом случае P(A) одна и та же во всех испытаниях. Во-втором случае P(A) изменяется от испытания к испытанию.

Задача. Производится n независим испытаний, найти вероятность того, что при этом A появл ровно m раз. Эту вероят обозн 

-событие, состоящее в том, что событие A в n испыт наступит ровно m раз. Обозн через  и  - появление или непоявление события A в i-ом испытании. 

- формула Бернулли.

Биномиальное распределение. ДСВ X имеет биномиальное распр, если она приним возм знач 0,1,2,...,n вероятностями  M(x)=np; D(x)=npq. Биномиальное распр явл отражением случ эксперимента когда последний можно представить в виде суммы 2-х точечного распр (закон Бернулли).

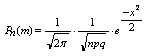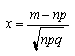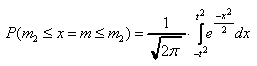, где  -локальная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа:  , где  ,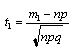 

 

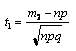
11

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

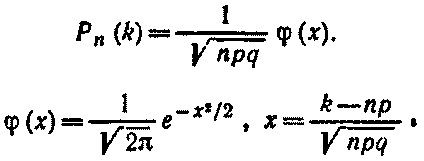
Для определения значений φ(x) можно воспользоваться специальной таблицей.

12

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

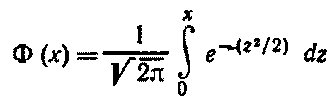
-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

Пример. Найти вероятность того, что событие А насту пит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение. По условию, n=243; k = 70; р =0,25; q= 0,75. Так как n=243 - достаточно большое число, воспользуемся локальной теоремой Лапласа:

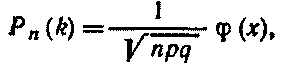
где х = (k—np)/ √npq.

Найдем значение х

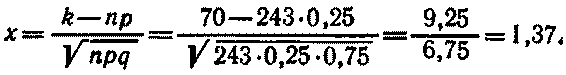
По таблице п найдем ф(1,37) =0,1561. Искомая вероятность

P(243)(70) = 1/6,75*0,1561 =0,0231.

13

Дискретные и непрерывные случайные величины

Дискретной называется случайная величина, которая при испытаниях может принимать одно из изолированных значений, количество которых конечно. К ним относятся величины из первой группы. Непрерывной называют случайную величину, которая в пределах ее изменения может принимать любые значения , которые могут быть конечными или бесконечными . К ним относятся величины из второй группы. Случайные величины принято обозначать заглавными буквами латинского алфавита: ..., X,Y,Z Конкретное значение, которое случайная величина (не важно какая – дискретная или непрерывная) приняла при испытании (опыте) принято обозначать как x1, x2, x3 ,...; y1, y2, y3 ,...; z1, z2, z3,... . Для дискретной случайной величины принято также обозначать X = {x1, x2, …, xn },

14

Закон распределения дискретной случайной величины

            Определение.  Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

            Закон распределения может быть задан аналитически, в виде таблицы или графически.

            Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

            Графическое представление этой таблицы называется многоугольником распределения.  При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

 

15

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

(binomial distribution) Распределение, позволяющее рассчитать вероятность наступления какого-либо случайного события, полученного в результате наблюдений ряда независимых событий, если вероятность наступления, составляющих его элементарных событий известна и постоянна. Если вероятность события (например, выпадения "решки" при бросании монеты или "шестерки" при бросании кубика) всякий раз равна р, а вероятность ненаступления этого события равна (1-р), то биномиальное распределение показывает, что вероятность наступления данного события раз при числе попыток n r, где 0 < r < n задается формулой рr(1-p)n-rnCr, где nСr обозначает число возможных способов выбора r объектов из n. nСr=n!/r!(n - r)!, где r!=r(r- 1)(r- 2) ...(2)(1) – r – факториал.

16

Распределение Пуассона - это дискретное распределение, являющееся одним из важных предельных случаев биномиального распределения. При росте n и зафиксированном значении произведения np=λ > 0 биномиальное распределение B(n,p) сходится к распределению Пуассона. Таким образом, случайная величина, имеющая распределение Пуассона с параметром λ, принимает неотрицательные целые значения с вероятностью

Интегральная функция вероятности распределения равна

Параметр λ является одновременно и математическим ожиданием, и дисперсией случайной величины, имеющей распределение Пуассона.

Классическим примером случайной величины, распределенной по Пуассону, является количество машин, проезжающих через какой-либо участок дороги за заданный период времен. Также можно отметить такие примеры, как количество звезд на участке неба заданной величины, количество ошибок в тексте заданной длины, количество телефонных звонков в call-центре или количество обращений к веб-серверу за заданный период времени.

17

Поток событий называется простейшим, если он стационарен, однороден и не имеет последействия. Для такого потока вероятность появления на интервале   m событий определяется формулой Пуассона     -средняя интенсивность потока.

18

ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ - распределение дискретной случайной величины, принимающей целые неотрицательные значения m = 0, 1, ... с вероятностями p_m = pq^m, где параметр распределения р = 1 - q есть нек-рое число из интервала (0, 1). Характеристич. функция:

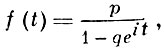
математич. ожидание: q/p, дисперсия: q/p²; производящая функция:

Г. р. имеет случайная величина, равная числу независимых испытаний до первого успеха, если вероятность успеха равна р, а неудачи q. Свое название Г. р. получило от порождающей его геометрич. прогрессии.

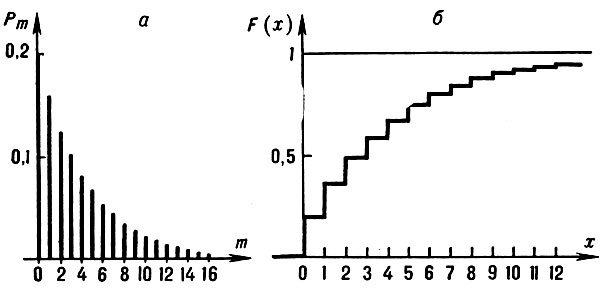
Геометрическое распределение: a - вероятности p_m, б - функция распределения (р = 0,2).

19

ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ - распределение вероятностей, заданное формулой

(*)

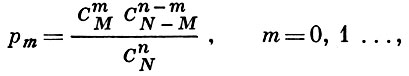
где М, N и n - целые неотрицательные числа и М ≤ N, n ≤ N (здесь С^b_a - биномиальный коэффициент). Г. р. обычно связано с выбором без возвращения, а именно: формула (*) указывает вероятность получения ровно m «отмеченных» элементов в случайной выборке объема n из генеральной совокупности, содержащей N элементов, среди к-рых М «отмеченных» и N - M «неотмеченных» элементов. При этом вероятность (*) определена лишь для

max(0, М + n - N) ≤ m ≤ min (n, М).

Однако определение (*) можно использовать при всех m ≥ 0, т. к. можно считать, что С^b_a = 0 при b > а, поэтому равенство Р_m = 0 нужно понимать как невозможность получить в выборке m «отмеченных» элементов. Сумма значений р_m, распространенная па все выборочное пространство, равна 1. Если обозначить M/N = p, то (*) можно переписать в иной форме:

где

Если р постоянна и N → ∞, то имеет место биномиальное приближение

Среднее значение Г. р. не зависит от N и совпадает со средним пр. соответствующего биномиального распределения Дисперсия Г. р.

σ² = npq(N - n)/(N - 1)

не превосходит дисперсии биномиального закона σ² = npq. При N → ∞ моменты любого порядка Г. р. стремятся к соответствующим значениям моментов биномиального распределения. Производящая функция Г. р. имеет вид:

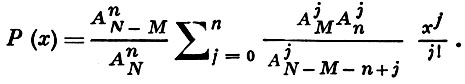
Ряд в правой части представляет собой гипергеометрическую функцию Р(α, β, γ, х), где α = -n, β = -M, γ = N - М - n + 1 (этому обстоятельству распределение обязано своим названием). Вероятность (*) и соответствующая функция распределения табулированы в широких пределах.

20