14. Поняття кільця, поля. Види кілець. Кільце квадратних матриць, кільце класів лишків, кільце многочленів.

Означення. Кільцем наз. непорожня множина , в якій визначено дві бінарні алгебраїчні операції – додавання і множення, причому за додаванням є абелева група – адитивна група кільця , а операція множення – асоціативна і пов’язана дистрибутивними законами з операцією додавання.

Означення. Комутативне кільце з одиницею, в якому для кожного його ненульового елемента обернений елемент наз. полем.

Означення. Підмножина кільця наз. підкільцем кільця , якщо є кільцем відносно операцій додавання та множення, визначених у кільці .

Число довгий час вважалося містичним, однак виявилося, що існують аналоги цього числа, які є абсолютно реальними об’єктами. Розглянемо множину квадратних матриць виду:

Покажемо, що ця множина матриць утворює кільце. В цій множині існує матриця О –нульовий елемент. Е – одинична матриця.

Асоціативність додавання і множення, комутативність додавання та дистрибутивність множення випливає з виконання даних властивостей квадратних матриць. Отже, Р утворює кільце. Оскільки множення матриць даного типу є комутативним, то кільце Р – комутативне.

Означення. Непорожня підмножина кільця наз. лівим(правим) ідеалом цього кільця, якщо виконуються такі умови:

1) , де ;

2) , де .

Відношення конгруентності елементів на множині деякого кільця за його ідеалом є бінарним відношенням еквівалентності. Класи еквівалентності наз. ще класами лишків кільця за ідеалом . Множину всіх класів лишків кільця за ідеалом його позначають . У цій множині алгебраїчними є операції додавання і множення класів лишків:

, .

Відносно цих операцій множина утворює кільце, яке наз. фактор-кільцем кільця за ідеалом . Фактор-кільце наз. ще кільцем класів лишків.

Нехай – довільна область цілісності з одиницею і – її підкільце з одиницею. Елемент наз. алгебраїчним над кільцем , якщо в існують такі елементи , які не всі дорівнюють нулю, що:

Елемент, який не є алгебраїчним над є трансцендентним над .

Означення. Мінімальне розширення кільця , яке містить трансцендентний над елемент х, наз. кільцем многочленів від однієї змінної над і позначається [x].

Означення. Кільцем многочленів від п змінних над областю цілісності наз. кільце многочленів від змінної над кільцем .

Векторний простір над полем, приклади. Поняття векторного підпростору та фактор-простору, способи їх задання.. Поняття базису векторного простору, еквівалентність різних означень.

Вектор - елемент векторного простору.

Вектором розмірності n будемо називати послідовність   з n елементів деякого заданого поля P, розташованих у вказаному порядку.

Сума векторів обчислюється покоординатно:  .

Добуток на скаляр теж:  .

Сукупність усіх n-вимірних векторів виду  , на якій визначено дії додавання та множення на скаляр, називається арифметичним векторним простором.

Лінійним (або векторним) простором над полем P називається множина математичних об'єктів V з визначеними на ній операціями додавання та множення на елементи поля Р, які задовольняють наступним аксіомам:

• .

• .

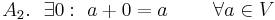•  (0 - нейтральний елемент відносно додавання).

•  (-a - протилежний елемент).

• .

• .

• .

•  (1 - нейтральний елемент відносно множення).

Елементи множини V називаються векторами.

приклади:

• С([a,b]) - множина всіх неперервних на [a; b] функцій.

• простір всіх многочленів не вище n-го степеня.

Векторний підпростір - це підмножина векторного простору  , яка задовольняє такі умови:

• ,

• .

Фактор-простір : нехай W підпростір V, тобто  . Тоді 2 елементи  , що  , називаються еквівалентними. Це позначається  . Отриманий в результаті факторизації простір   називають факторпростором по підпростору W. (з рос. вікі)

TODO: написати цей пункт!

Нехай   - деякі числа,   - деякі вектори.

Вектор   називається лінійною комбінацією векторів  .

Система векторів   називається лінійно залежною, якщо існують числа  , не всі рівні 0, такі, що  .

Система векторів   називається лінійно незалежною, якщо рівність   можлива тільки тоді, коли всі числа λ дорівнюють 0.

Підсистема векторів   системи   називається породжуючою підсистемою, якщо всі інші вектори системи є лінійними комбінаціями векторів  .

Породжуюча підсистема називається мінімальною породжуючою, якщо після вилучення з неї будь-якого вектора вона перестає бути породжуючою.

Підсистема векторів називається максимальною лінійно незалежною, якщо після додавання до неї будь-якого вектора системи вона стає лінійно залежною.

Теорема. Максимальна лінійно незалежна підсистема векторів є мінімальною породжуючою і навпаки.

Мінімальна породжуюча (максимальна лінійно незалежна) підсистема системи векторів називається базою системи векторів.

Мінімальна породжуюча (максимальна лінійно незалежна) система векторів простору V називається базисом простору V.