
- •1.Системи лінійних рівнянь
- •1.Системи лінійних рівнянь
- •2.Матриці і дії над ними. Обернена матриця. Матричний метод розв’язування систем лінійних рівнянь.
- •2.Матриці і дії над ними
- •9.Евклідів простір. Нерівність Коші-Буняковського.
- •12. Поняття групи, підгрупи. Циклічні групи. Фактор-група.
- •15. Поле. Характеристика поля. Поле раціональних дробів. Побудова скінчених полів з допомогою фактор-кілець.
- •14. Поняття кільця, поля. Види кілець. Кільце квадратних матриць, кільце класів лишків, кільце многочленів.
- •Векторний простір над полем, приклади. Поняття векторного підпростору та фактор-простору, способи їх задання.. Поняття базису векторного простору, еквівалентність різних означень.
- •Криві другого порядку: означення, властивості.
- •Рівняння прямої на площині та в просторі. Векторний та мішаний добуток векторів.
- •[Ред.]Види рівнянь площини в просторі. Векторний та мішаний добуток векторів.
- •1. Поняття бінарної алгебраїчної операції
- •2. Властивості бінарних алгебраїчних операцій
- •Операції над множинами та їх властивості.
- •Відношення еквівалентності
- •Комплексні числа та дії над ними
2.Матриці і дії над ними
Операція знаходження добутку матриць і називається операцією множення матриць і .
Властивості операції множення матриць:
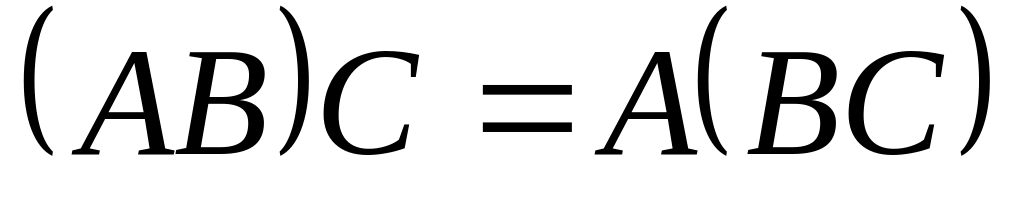 (асоціативна
властивість).
(асоціативна
властивість). (дистрибутивна
властивість першого
множника).
(дистрибутивна
властивість першого
множника). (дистрибутивна
властивість другого
множника).
(дистрибутивна
властивість другого
множника).
Якщо
![]()
![]() ,
то матриці називаються комутативними.
,
то матриці називаються комутативними.
Транспонування.
Нехай
дана матриця (1). Матриця
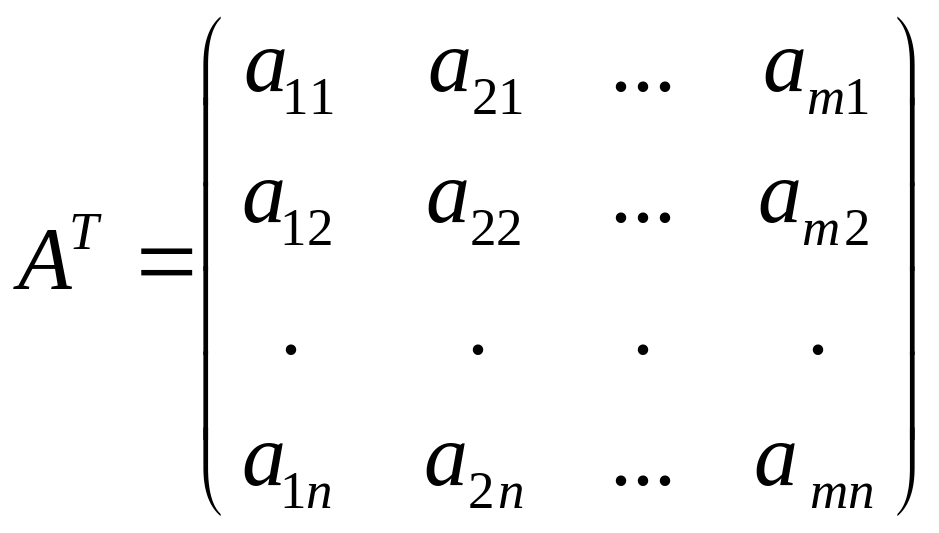 ,
здобута із
заміною рядків на стовпці зі збереженням
порядку їх слідування, називається
транспонованою матрицею до
.
Операція заміни матриці
на
,
здобута із
заміною рядків на стовпці зі збереженням
порядку їх слідування, називається
транспонованою матрицею до
.
Операція заміни матриці
на
![]() називається
транспонуванням матриці
.
Властивості
транспонування матриці:
називається
транспонуванням матриці
.
Властивості
транспонування матриці:
Якщо
квадратна матриця
![]() збігається
зі своєю транспонованою матрицею
збігається
зі своєю транспонованою матрицею
![]() ,
то
така матриця називається
симетричною.
Якщо
квадратна матриця
,
то
така матриця називається
симетричною.
Якщо
квадратна матриця
![]() відрізняється
знаком
від своєї транспонованої матриці
відрізняється
знаком
від своєї транспонованої матриці
![]() ,
тобто
,
тобто![]() ,
то така матриця називається кососиметричною.
,
то така матриця називається кососиметричною.
Цілим
додатним степенем
![]() квадратної
матриці
є
добуток
матриць,
рівних
.
квадратної
матриці
є
добуток
матриць,
рівних
.
Нехай — квадратна матриця n-го порядку.
Квадратна матриця С порядку n називається оберненою до матриці , AC=CA=E, де E— одинична матриця n-го порядку.
Матриця,
обернена до матриці
,
позначається
через
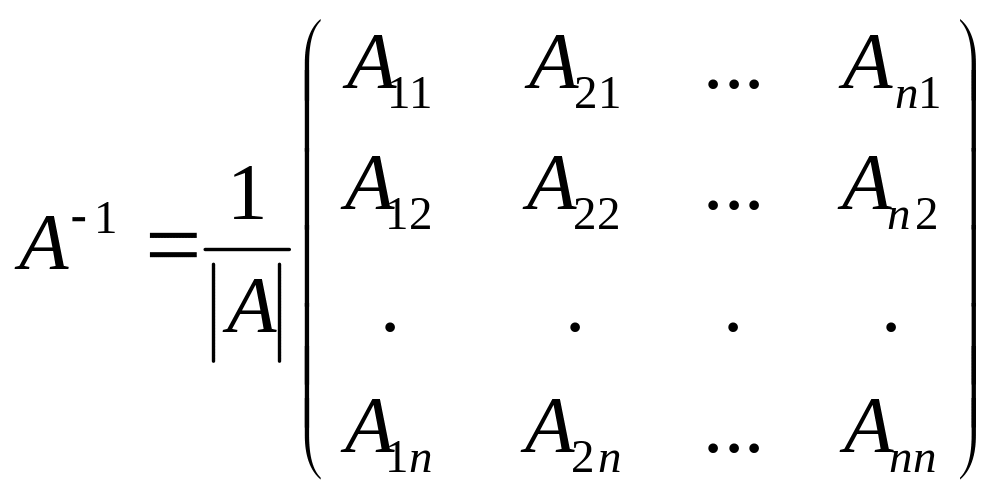 ,
де
,
де
![]() – алгебраїчне доповнення елемента
– алгебраїчне доповнення елемента
![]() матриці
.
матриці
.
Квадратна
матриця
порядку
n
називається
особливою,
якщо її детермінант дорівнює нулю.
Якщо![]() ,
то
називається
неособливою.
,
то
називається
неособливою.
ТЕОРЕМА 1.1. Особливі матриці обернених матриць не мають. Кожна неособлива матриця має єдину обернену матрицю.
Матричний метод. Розглянемо систему n лінійних алгебраїчних рівнянь з n невідомими:
 .
Якщо
.
Якщо
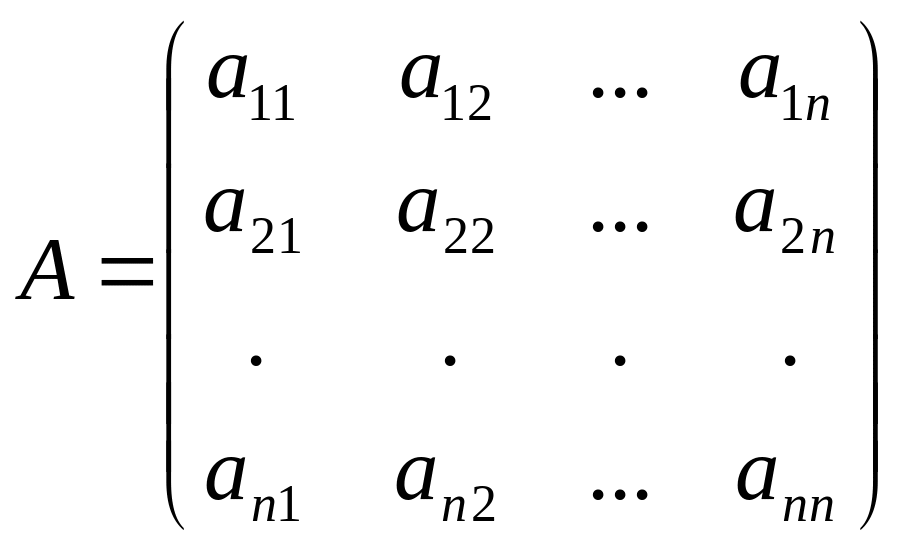 ,
,
 ,
,
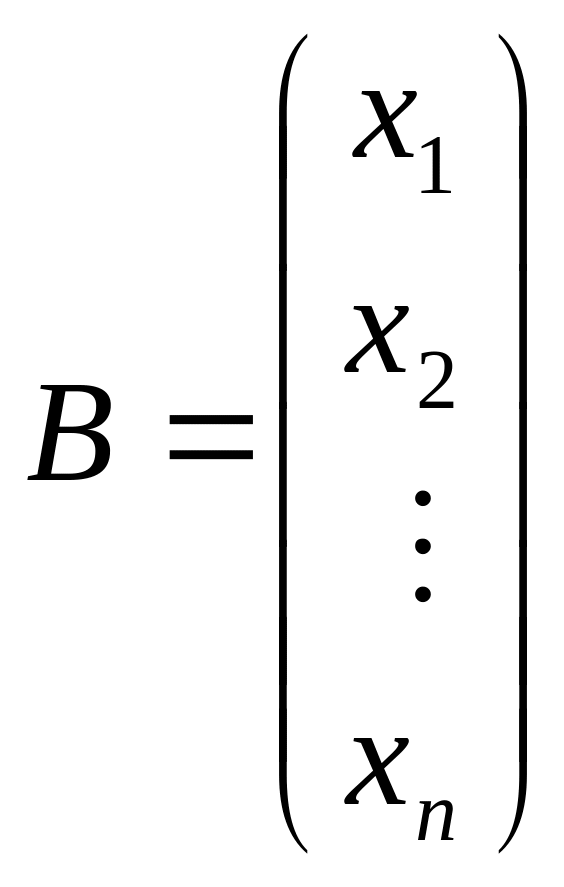 ,
то в матричній формі система має вигляд
,
то в матричній формі система має вигляд
![]() .
Якщо
, то розв’язок
системи має вигляд
.
Якщо
, то розв’язок
системи має вигляд
![]() .
.
9.Евклідів простір. Нерівність Коші-Буняковського.
Лінійний
простір
![]() називається евклідовим простором, якщо
виконуються наступні умови:
називається евклідовим простором, якщо
виконуються наступні умови:
Будь-яким двом елементам даного простору
 і
і
 ставиться у відповідність дійсне число,
яке називається скалярним добутком
цих елементів і позначають символом
ставиться у відповідність дійсне число,
яке називається скалярним добутком
цих елементів і позначають символом
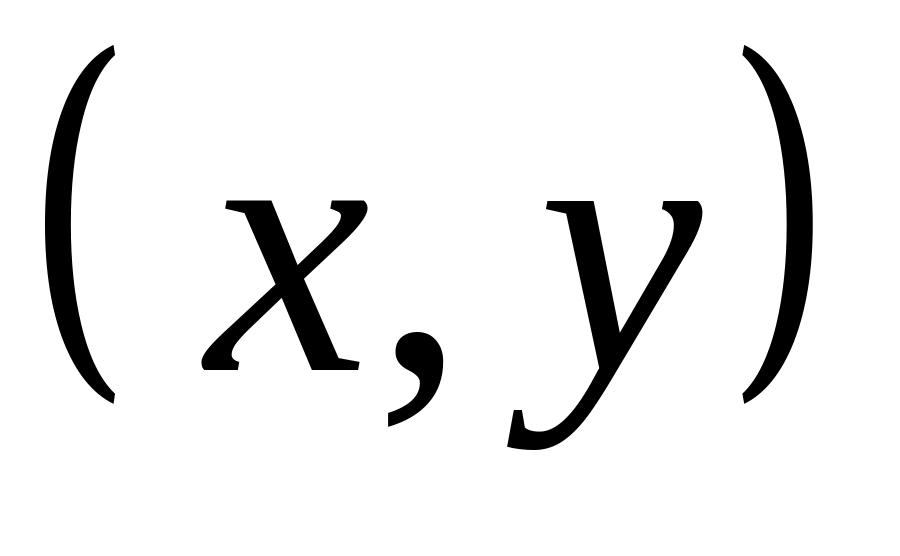 .
.Для скалярного добутку справедливі такі аксіоми:
2.1
![]() -
аксіома симетрії
-
аксіома симетрії
2.2
![]() -
аксіома роз подільності
-
аксіома роз подільності
2.3
![]() ,
для будь-якого дійсного числа
,
для будь-якого дійсного числа
![]()
2.4
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Теорема1:Для
будь-яких двох елементів
![]() і
і
![]() довільного евклідового простору
справедлива нерівність
довільного евклідового простору
справедлива нерівність
![]() ,
яка називається нерівністю
Коші-Буняковського.
,
яка називається нерівністю
Коші-Буняковського.
Доведення:
для будь-якого дійсного числа
![]() , в силу аксіоми 2.4 скалярного добутку,
справедлива рівність
, в силу аксіоми 2.4 скалярного добутку,
справедлива рівність
![]() .
В силу аксіом 2.1-2.3, останню рівність
можна записати в вигляді
.
В силу аксіом 2.1-2.3, останню рівність
можна записати в вигляді
![]() . Для того щоб виконувалась дана рівність
необхідно і достатньо щоб дискримінант
даного тричлена був недодатнім, тобто
щоб виконувалась рівність
. Для того щоб виконувалась дана рівність
необхідно і достатньо щоб дискримінант
даного тричлена був недодатнім, тобто
щоб виконувалась рівність
![]() ,
звідки випливає потрібна рівність.
Теорема
доведена.
,
звідки випливає потрібна рівність.
Теорема
доведена.
Теорема2:
Для будь-яких двох елементів
і
довільного комплексного евклідового
простору справедлива нерівністю
Коші-Буняковського
![]()
Доведення:
для будь-якого комплексного числа
, в силу аксіоми 2.4 скалярного добутку,
справедлива рівність
.
В силу аксіом 2.1-2.3, останню рівність
можна записати в вигляді
![]()
![]() . Позначимо через
. Позначимо через
![]() аргумент комплексного числа
аргумент комплексного числа
![]() і представимо в вигляді
і представимо в вигляді
![]() .
Тоді
.
Тоді
![]() ,
де
,
де
![]() -будь-яке
дійсне число.
-будь-яке
дійсне число.
![]() ,
,
![]() .
Отримаємо наступну рівність
.
Отримаємо наступну рівність
![]() .
Яка справедлива для будь-якого дійсного
.
Для того щоб виконувалась дана рівність
необхідно і достатньо щоб дискримінант
даного тричлена був недодатнім, тобто
щоб виконувалась рівність
.
Яка справедлива для будь-якого дійсного
.
Для того щоб виконувалась дана рівність
необхідно і достатньо щоб дискримінант
даного тричлена був недодатнім, тобто
щоб виконувалась рівність
![]() ,
звідки випливає потрібна рівність.
Теорема
доведена.
,
звідки випливає потрібна рівність.
Теорема
доведена.
