Комплексні числа та дії над ними

Комплексним числом називається впорядкована пара дійсних чисел . Число називається дійсною частиною комплексного числа та позначається , називається уявною частиною та позначається . Операції додавання та множення комплексних чисел виконуються за такими правилами:

;

.

Будемо вважати, що дійсні числа є частинним випадком комплексних чисел. Якщо ототожнити дійсне число з комплексним числом та назвати пару числом – уявною одиницею, то число можна записати у вигляді

.

Така форма запису комплексного числа називається алгебраїчною, а дії додавання та множення з числами в алгебраїчній формі зводяться до стандартних перетворень з урахуванням рівності .

Число називається числом, спряженим до числа . Добуток спряжених комплексних чисел є дійсним числом :

.

Ділення комплексних чисел виконується шляхом домноження числівника та знаменника дробу на число, спряжене до знаменника:

.

Геометричним образом комплексного числа є точка на координатній площині з відповідними декартовими координатами. Полярні координати цієї точки також є важливими характеристиками комплексного числа. Відповідний полярний радіус називається модулем комплексного числа, а полярний кут – його аргументом:

, .

Тригонометрична форма комплексного числа

Кожному комплексному числу відповідає деякий вектор на площині, а будь-який вектор задається довжиною і напрямком. Наприклад вектор можна задати кут якій цей вектор утворює з додатним напрямком осі . Домомвимось, що всі кути відраховуються від осі проти годинникової стрілки.

Нехай `відповідає комплексному числу позначимо через довжину вектора , а через кут, який утворює цей вектор з додатним напрямком осі , тоді

- тригонометрична форма комплексного числа.

Назвемо - модулем комплексного числа , а - аргумент комплексного числа ( , якщо , то аргумент не визначається).

Нехай , тоді

Для даного комплексного числа його модуль визначається точно, а аргумент з точністю до періода. Таким чином два числа в тригонометричні формі вважаються рівними, якщо їх модулі рівні, а аргументи відрізняються на число кратне

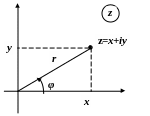
Дійсна та уявна частини комплексного числа зв’язані з його модулем та аргументом співвідношеннями , .

Як відомо, кожній точці координатної площини відповідає безліч значень полярного куту, які відрізняються одне від одного на , де – ціле число.

Для однозначного визначення аргументу комплексного числа будемо обирати його з певного проміжку довжиною . Таке значення аргументу називається його головним значенням та позначається . Будемо вважати, що належить проміжку (досить часто також використовують проміжок ).Тоді модуль та головне значення аргументу комплексного числа доцільно обчислювати за формулами

;

або .

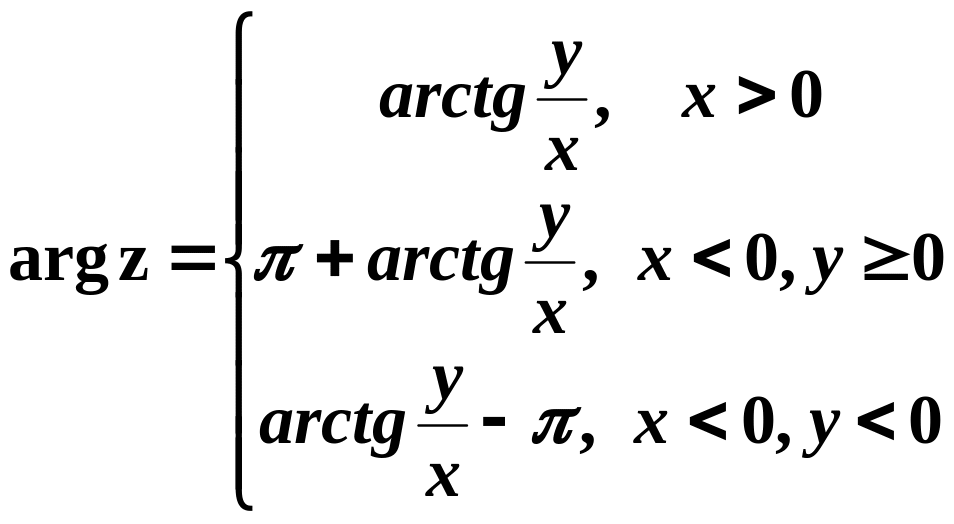З урахуванням наведених вище співвідношень комплексне число можна представити у вигляді

.

Така форма запису комплексного числа називається тригонометричною, а множення, ділення та піднесення до натурального степеня виконуються за формулами

;

;

.

З урахуванням формули Ейлера комплексне число може бути записано у показниковій формі

.

Якщо комплексні числа записані у показниковій формі, то дії множення, ділення та піднесення до натурального степеня виконуються за правилами

;

;

.

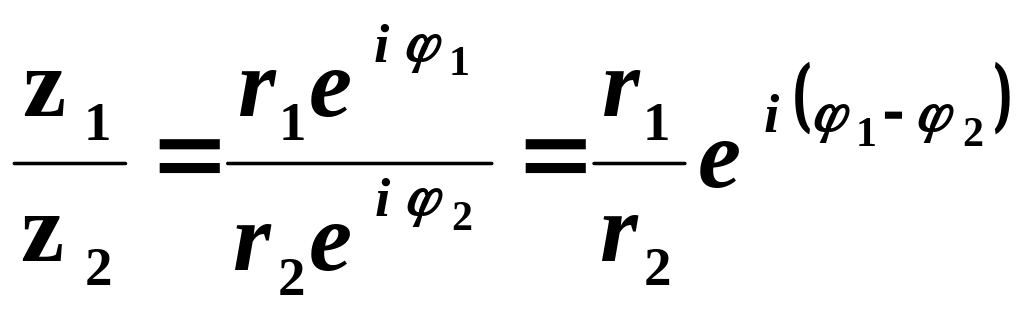Коренем -го степеня з комплексного числа називається таке число, -ий степінь якого дорівнює . Обчислення кореня виконується за формулою

, ,

тобто корінь -го степеня має значень.

Формула Муавра

Пусть комплексное число z представлено в тригонометрической форме: z = r(cosφ + i sinφ), где r – модуль данного числа, а φ его аргумент. Поскольку при умножении комплексных чисел их модули умножаются, а аргументы складываются, имеем: z2 = r2(cos2φ + i sin2φ), z3 = r3(cos3φ + i sin3φ), … Поэтому легко доказать (например, методом полной математической индукции) формулу Муавра, имеющую вид zn = rn(cosnφ + i sinnφ). С помощью формулы Муавра можно получить формулы, выражающие cosnφи sinnφ через синус и косинус числа φ: здесь   – биномиальные коэффициенты. Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.