2. Властивості бінарних алгебраїчних операцій

1. Означення. Операція на множині називається комутативною, якщо .

Приклади.

1. Додавання і множення чисел комутативні.

2. Віднімання і ділення чисел некомутативні.

3. Множення матриць некомутативне.

4. Операції перерізу і об’єднання множин комутативні.

5. Операція декартового добутку двох множин некомутативна.

Значення комутативності бінарної алгебраїчної операції полягає в тому, що вона дає можливість переставляти елементи, над якими виконується бінарна операція, і завдяки цьому спрощувати формули і твердження.

Таблиця Келі комутативної бінарної алгебраїчної операції симетрична відносно діагоналі.

Приклад 1. Операція у множині з прикладу 1 є комутативною, оскільки її таблиця Келі симетрична відносно діагоналі.

2. Означення. Операція на множині називається асоціативною, якщо

: .

Властивість асоціативності дозволяє опускати дужки у виразі .

Приклади.

1. Додавання і множення чисел асоціативні. Це дозволяє не ставити дужки у виразах і .

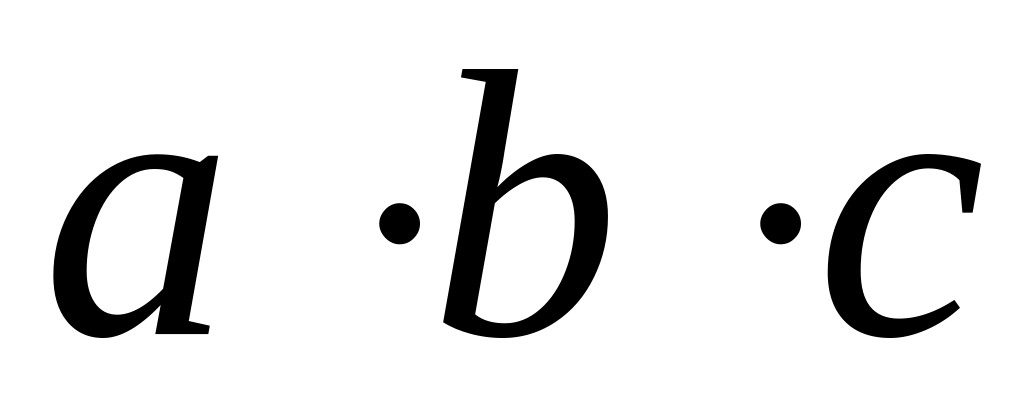2. Віднімання чисел неасоціативне.

(Наприклад, )

3. Операції перерізу і об’єднання множин асоціативні.

Значення асоціативності бінарної алгебраїчної операції полягає в тому, що вона дає можливість визначити композицію трьох і взагалі будь-якого числа елементів множини, взятих у певному порядку.

3. Означення. Операція на множині називається дистрибутивною зліва відносно операції , якщо

і дистрибутивною справа відносно операції , якщо

.

Властивість дозволяє розкривати дужки.

Якщо операція комутативна на множині , то поняття дистрибутивності зліва і справа збігаються. В цьому випадку просто кажуть, що операція дистрибутивна відносно операції .

Приклади.

1. Множення чисел дистрибутивне відносно додавання і зліва і справа:

і

2. Додавання недистрибутивне і зліва і справа відносно множення:

та .

3. Операції перерізу і об’єднання множин є взаємно дистрибутивними одна відносно одної.

Далі будемо припускати, що всі бінарні операції, які будуть розглядатися, асоціативні. В цьому випадку неважко визначити степінь елемента множини у такий спосіб: визначаємо , при покладаємо: . Тоді для будь-яких додатних цілих чисел виконуються співвідношення:

і .

Разом з бінарними алгебраїчними операціями не позбавлені інтересу більш загальні -арні операції, так само як і їх комбінації.

Означення. -арною алгебраїчною операцією на множині називається відображення . Число називається арністю операції .

–арна алгебраїчна операція за елементами множини визначає -й елемент цієї ж множини. При будемо мати відповідно унарну, бінарну, тернарну і т.д. алгебраїчні операції.

Приклади.

1. Перехід до протилежного числа є унарною операцією.

2. Піднесення числа до квадрату є унарною операцією.

3. Знаходження абсолютної величини числа є унарною операцією.

4. Операція доповнення множини є унарною операцією.

5. Поняття множини відноситься до фундаментальних невизначених понять математики

6. Множина - однозначно визначена сукупність елементів довільної природи.

7. Для позначення множини будемо вживати великі літери А, В, С, D, а для їх елементів - маленькі літери a, b, c, d

8. Порожня множина - множина, що не містить жодного елемента (позначення -  ). Для будь-якої множини порожня множина є її підмножиною.

9. Множина А називається підмножиною множини В, якщо кожен елемент з множини А лежить в множині В.

10.  Позначається 

11. Множини А і В називається рівними, коли   і