§ 54. Элементы взаимного ориентирования пары аэроснимков

При обработке результатов фотограмметрических измерений при­меняют две ос­новные сис­темы элементов взаимного ориентирова­ния, различающиеся способом ориенти­рования: накло­нами и враще­ния­ми обоих снимков при неподвижном базисе или наклонами и вра­ще­ниями од­ного снимка и базиса фотографирования.

В базисной системе (рис. 8.4) неподвижным (горизон­тальным) считается базис фотогра­фи­ро­вания. Начало фотограмметри­ческой сис­темы коор­динат совмещено с центром проекции ле­вого снимка S₁, ось абсцисс S₁X₁ совмещена с базисом фотографирования S₁S₂, а плос­кость S₁X₁Z₁ – с главной базис­ной плоскостью ле­вого снимка. Элементами взаимного ори­енти­рова­ния являются:

₁ – угол в плос­кости S₁X₁Z₁ между главным оптическим лу­чом So и осью S₁Z₁;

₁ – угол в плос­кости левого снимка P₁ между осью o₁y₁ и сле­дом сечения снимка плос­ко­стью S₁o₁Y₁;

₂ – угол в плоскости S₁X₁Z₁ между осью S₁Z₁ (S₂Z₂) и проекцией правого глав­ного оптиче­ского луча S₂o₂ на плоскость S₁X₁Z₁;

₂ – угол в плоскости S₂Y₂o₂ между главным оптическим лучом пра­вой связки S₂o₂ и плос­ко­стью S₁X₁Z₁;

₂ – угол в плоскости правого снимка P₂ между осью o₂y₂ и следом сечения снимка плоско­стью S₂o₂Y₂.

У глы ₁ и ₂ называются продольными углами наклона соответст­венно левого и пра­вого снимков относительно базиса фото­гра­фи­ро­ва­­ния, ₂ – взаимным поперечным углом на­клона, а углы ₁ и ₂ – уг­лами поворота.

В линейно-угловой системе (рис. 8.5) неподвижным считается левый сни­мок. Начало фотограмметрической сис­темы коор­динат совмещено с центром проекции ле­вого снимка S₁, координат­ные оси X₁ и Y₁ направлены параллельно осям координат x₁ и y₁ ле­вого снимка, а ось Z₁ является про­должением главного оптического луча ле­вой связки. Система координат S₂X₂Y₂Z₂ парал­лельна сис­теме S₁X₁Y₁Z₁. Элементами взаимного ориентирова­ния явля­ются:

 – угол в плоско­сти P₁ между осью x₁ и сле­дом сечения главной ба­зисной плос­костью ле­вого снимка;

 – угол наклона базиса фотографи­рования в плоско­сти S₁S₂o₁ ме­жду перпендикуляром к нему и осью S₁Z₁;

 – взаимный про­дольный угол на­клона в плос­кости S₂X₂Z₂ между осью S₂Z₂ и проекцией глав­ного луча пра­вой связки на плос­кость X₂Z₂;

 – взаимный поперечный угол на­клона в плоскости S₂Y₂o₂ между главным оптиче­ским лу­чом правой связки S₂o₂ и его проекцией на плоскость X₂Z₂;

 – взаимный угол поворота в плоскости правого снимка P₂ между осью y₂ и следом плоско­сти S₂o₂Y₂.

Обе системы отсчетов элементов взаимного ориентирования точно соот­ветствует системе от­счета угловых элементов внешнего ориенти­рова­ния снимков (§ 20), поэтому связь внут­рен­них и внешних коорди­нат точек описывается полученными в § 22 формулами.

§ 55. Уравнение взаимного ориентирования

О дной из важнейших задач фотограмметрии является взаим­ное ориентирование снимков. Основание для ее решения было пред­ло­жено С. Финстервальдером в 1899 г. как условие пере­сечения в простран­стве пары соответственных лучей. Аналитическое решение задачи пред­ло­жено профессором А.С. Скири­довым в 1928 г.

На рис. 8.6 изображена пара сним­ков P₁ и P₂ и связки про­ектирую­щих лучей в том поло­жении, которое они занимали в момент фотогра­фиро­вания. Любая пара соответствен­ных лу­чей (например, S₁m₁ и S₂m₂) пересекается и находится в одной плоско­сти, проходя­щей че­рез базис фотографирования S₁S₂. Если изменить положение одной из связок про­ек­тирую­щих лучей, то соответственные лучи ока­жутся в разных плоско­стях, в точке M не пере­секутся, и модель разру­шится.

Следовательно, условием взаимного ориентирования пары сним­ков является размещение соответственных векторов в од­ной базисной плоскости и их пере­сечение в одной точке. Мате­мати­чески это описы­вается условием ком­планар­ности век­торов R₁,R₂ и R₀ , т. е. усло­вием равенства нулю их векторно-ска­лярного произведения, численно равного объему построенного на этих векторах параллеле­пи­педа:

. (8.1)

Уравнение (8.1) связывает направле­ния векто­ров, любой из них можно разделить на свой модуль, потому

. (8.2)

Вид уравнения взаимного ориентирования в матричной и в коорди­натной форме зависит от выбора координатной системы, отно­сительно которой опре­деляются элементы взаимного ори­ентирования. Так, при­менительно к базисной сис­теме (рис. 8.4) уравне­ние (8.2) в мат­ричной форме имеет вид:

, (8.3)

где в соответствии с (3.4)

, . (8.4)

Здесь B – базис фотографирования; X₁,Y₁,Z₁ и X₂,Y₂,Z₂ – коорди­наты точек m₁ и m₂ в сис­темах S₁X₁Y₁Z₁ и S₂X₂Y₂Z₂; b_i, c_i, b_i, c_i (i=1,2,3)  направ­ляю­щие косинусы, опреде­ляемые по форму­лам (3.8) с заменой углов , ,  на ₁, ₁=0, ₁ для левого снимка и на ₂, ₂, ₂ для правого.

Получим уравнение взаимного ориентирования в координатной форме, для чего раз­делим первую строку определителя (8.3) на вели­чину B и раскроем его:

Y₁Z₂ – Y₂Z₁=0. (8.5)

Умножив это уравнение на (f/Z₁Z₂), после несложных преобра­зований с уче­том (3.21) и (3.4) получим еще одну форму за­писи урав­нения взаимного ориентирования:

. (8.6)

Полученное уравнение интерпретируется как условие равен­ства нулю поперечных парал­лаксов точек трансфор­миро­ванных снимков или условие равенства их трансформированных орди­нат. Последнее и объясняет отсутст­вие поперечных параллаксов при стереоскопических на­блю­дениях эпи­полярных изображений.

Приведем уравнение (8.5) к линейному виду, содержащему эле­менты взаимного ориен­ти­ро­вания в явном виде, для чего подставим в него ко­ор­динаты соответст­вен­ных точек (8.4) и на­правляющие коси­нусы. С этой целью заменим в формулах (3.8) тригонометрические функции углов ,  и  их разло­жениями в ряды с удержанием чле­нов первого порядка мало­сти:

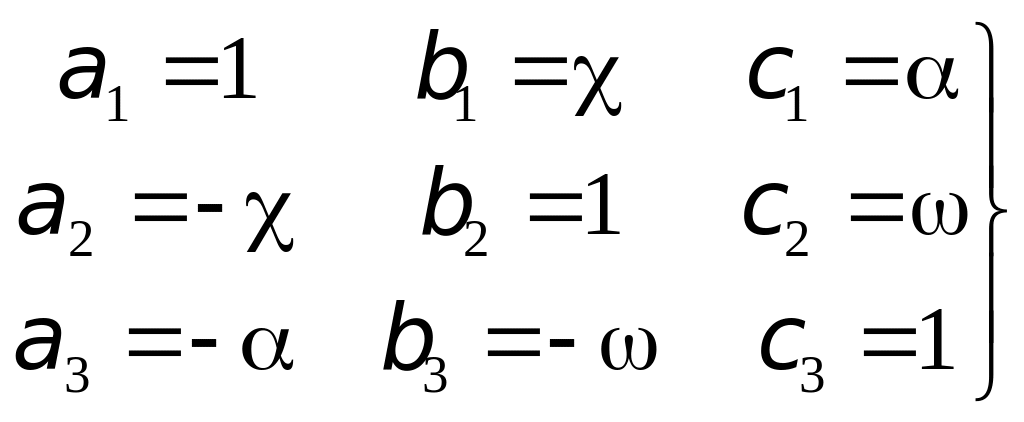. (8.7)

Подставка этих значений в (8.4) и (8.5) с учетом замены ,  ,  на ₁, ₁=0, ₁ для ле­вого снимка и на ₂, ₂, ₂ для правого снимка дает:

.

Полагая y₁=y₂=y и раскрывая скобки, после ряда преобразо­ваний получим урав­нение вза­имного ориентирования в ли­нейном виде:

. (8.8)

Применительно к линейно-угловой системе (рис. 8.5) урав­нение взаимного ориен­ти­рования в матричной форме будет иметь вид

, или .

После приведения его к линейному виду рассмотренным выше способом получим

. (8.9)

Уравнения (8.8) и (8.9) пригодны для оп­ре­деления элементов вза­имного ориентирования только плановых сним­ков. Для этого изме­ряют координаты и парал­лаксы как минимум пяти точек, составляют для каждой из них уравнение (8.8) или (8.9) и решают полученную систему уравнений.