1.2. Скорость

Д ля характеристики движения материальной точки вводится векторная величина – скорость, которая определяет быстроту и направление ее движения в данный момент времени.

Пусть материальная точка движется по некоторой криволинейной траектории из положения А в положение В (рис. 1.2.1), заданные радиусами-векторами и соответственно. При этом точка пройдет путь . Ее перемещение будет равно .

Вектором средней скорости называют отношение перемещения к промежутку времени, за который это перемещение произошло:

. (1.2.1)

Направление средней скорости совпадает с направлением перемещения.

Средней путевой скоростью тела называется отношение пути к промежутку времени , в течение которого этот путь был пройден:

. (1.2.2)

Средняя скорость и средняя путевая скорость отличаются друг от друга так же, как отличается от , но при этом обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения .

Пример 1.2.1. Городской троллейбус утром вышел на маршрут, а через 8 часов, проехав в общей сложности 72 км, возвратился в парк и занял свое место на стоянке. Какова средняя скорость и средняя путевая скорость троллейбуса (в км/ч)?

Дано: Решение:

П

,

,

.

оскольку начальное и конечное положение троллейбуса совпадают, то его перемещение , следовательно (формула 1.2.1): .

Средняя путевая скорость троллейбуса (формула 1.2.2) не равна нулю: .

Ответ: , .

Пример 1.2.2. Любитель бега трусцой пробежал половину пути со скоростью . Затем половину оставшегося времени бежал со скоростью , а потом до конца пути шел пешком со скоростью . Определить среднюю скорость движения бегуна.

Д

, , .

ано: Решение:

И з условия задачи следует, что речь идет о средней путевой скорости. Разобьем весь путь на три участка , и (рис. 1.2.2). Время движения на каждом участке обозначим соответственно , и .

Средняя путевая скорость бегуна, согласно формуле 1.2.2, равна:

. По условию , и .

Время движения на отдельных участках: ; .

Подставляя эти значения в выражение для , получим

.

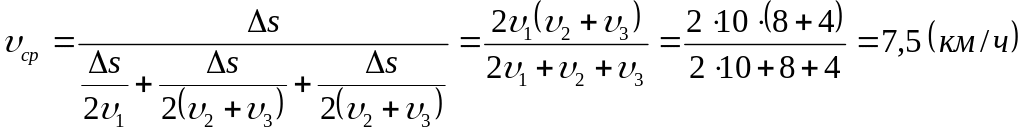О твет: .

Если брать все меньшие и меньшие промежутки времени , то отношение в пределе даст мгновенное значение скорости в данный момент времени:

.

Таким образом, мгновенная скорость – векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор мгновенной скорости направлен по касательной к траектории в сторону движения.

Учитывая 1.1.1, можно записать . (1.2.3)

По мере уменьшения путь все больше будет приближаться к , поэтому численное значение (модуль) мгновенной скорости:

.

Таким образом, численное значение мгновенной скорости равно первой производной пути по времени:

. (1.2.4)

Учитывая 1.2.3, получим

. (1.2.5)

Зная зависимость скорости от времени , можно найти зависимость пути, пройденного материальной точкой, от времени

.

При равномерном прямолинейном движении скорость точки не зависит от времени и остается постоянной в процессе движения как по модулю, так и по направлению.

В этом случае путь, пройденный точкой за промежуток времени от до , равен

, (1.2.6)

где путь, пройденный точкой к началу отсчета времени . Если начало координат совпадает с телом отсчета, то и .

Кинематическое уравнение движения будет иметь вид:

, (1.2.7)

где радиус-вектор тела в начальный момент времени .

В случае движения в одной плоскости (меняется две координаты), векторное

уравнение равносильно системе двух скалярных уравнений, выражающих зависимость от времени координат и движущегося тела:

(1.2.8)

где и начальные координаты тела в момент времени , а и проекции вектора скорости на координатные оси и соответственно.

А налитическое уравнение траектории, т.е. зависимость , получим, исключив временной параметр из системы уравнений 1.2.8: из первого уравнения системы найдем .

Подставим это значение во второе уравнение:

. (1.2.9)

Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 1.2.3), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: .

П ример 1.2.3. Равномерное прямолинейное движение на плоскости описывается уравнениями: , (величины измерены в СИ). Найти уравнение

т раектории тела. Построить график зависимости модуля вектора скорости от времени . Определите путь, пройденный телом в течение первых пяти секунд движения.

Дано: ,

,

.

Решение:

Сравнивая уравнения движения, представленные в условии задачи, с системой 1.2.8, находим:

, , , .

У равнение траектории получим, подставив эти значения в общее уравнение 1.2.9: .

Модуль скорости определим о формуле 1.2.5, зная и : .

График зависимости представлен на рис. 1.2.4. При равномерном прямолинейном движении пройденный путь , т.е. численно равен площади прямоугольника под графиком зависимости : .

О твет: (м), , .