Возведение в степень комплексных чисел

        Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или впоказательной форме.

1. ,

2. .

Для возведения комплексного числа в степень нужно модуль возвысить в эту степень, а аргумент умножить на показатель степени.

Извлечение корня

Определение. Корнем n -ой степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.

Из этого определения следует, что из равенства   следует равенство  .

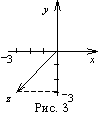         Из равенства комплексных чисел следует  , а аргументы отличаются на число, кратное   ; 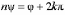 . Отсюда  ,  . Здесь   есть арифметическое значение корня, а k  – любое целое число. Таким образом, получается формула .

В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k  = 0, 1, 2, … , n  -  1.

        Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы 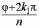  и 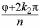 отличаются на величину, не кратную   , и будут одинаковыми, если указанные аргументы отличаются на величину, кратную  . Поэтому разность

не может быть кратна   .  Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.

Пусть теперь k₃–  целое число, не входящее в эту последовательность подряд взятых значений k . Это число можно представить в видеk₃= gn + k_i, где g  –  целое число, а k_i –  одно из чисел этого ряда, поэтому  , то есть значению k₃соответствует то же значение корня, что и значению k_i.

Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.

f = f(x) = a0 + a1x