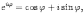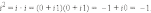- •30. Парабола, ее определение, уравнение.
- •31. Понятия алгебраической операции, группоида, полугруппы и группы.
- •41. Алгебраическая, тригонометрическая и показательная формы записи комплексных чисел. Алгебраическая форма
- •Сложение и вычитание
- •Умножение комплексных чисел
- •Деление комплексных чисел
- •Возведение в степень комплексных чисел
- •Извлечение корня
30. Парабола, ее определение, уравнение.
Параболой ( рис.1 ) называется геометрическое место точек, равноудалённых от заданной точки F , называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.
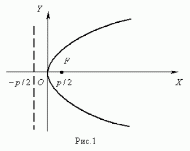
Уравнение параболы ( рис.1 ) :
y 2 = 2 p x .
Здесь ось ОХ является осью симметрии параболы.
Пусть Р ( х1 , у 1 ) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:
у 1 y = p ( x + х1 ) .
Условие касания прямой y = m x + k и параболы y 2 = 2 p x :
2 m k = p .
31. Понятия алгебраической операции, группоида, полугруппы и группы.
Определение. Соответствие, в силу которого каждой паре a, b элементов множества M, взятых в данном порядке, соответствует единственный третий элемент с того же множества M, называется алгебраической операцией, определенной в M.
32. Определение кольца и поля. Простейшие свойства колец и полей.
Определение кольца
Кольцом ![]() называется
множество элементов, на котором определены
две операции – сложение и умножение, и
в
выполняются
следующие аксиомы:
называется
множество элементов, на котором определены
две операции – сложение и умножение, и
в
выполняются
следующие аксиомы:
R.1. Множество является аддитивной абелевой группой.
R.2. Для любых двух элементов
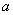 и
и  из
определено
их произведение:
из
определено
их произведение:  (замкнутость
операции умножения).
(замкнутость
операции умножения).R.3. Для любых трех элементов , и
 из
выполняется
ассоциативный закон, т.е.
из
выполняется
ассоциативный закон, т.е. 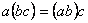 и
и  .
.R.4. Для любых трех элементов , и из выполняется дистрибутивный закон, т.е. справедливы равенства:
 и
и  .
.
Определение поля
Полем  называют
коммутативное кольцо с единицей, в
котором каждый ненулевой элемент имеет
мультипликативный обратный элемент
(т.е. обратный по умножению).
называют
коммутативное кольцо с единицей, в
котором каждый ненулевой элемент имеет
мультипликативный обратный элемент
(т.е. обратный по умножению).
Другими словами, полем называют множество, которое является аддитивной абелевой группой; ненулевые же элементы этого множества образуют мультипликативную абелевую группу, и выполняется закон дистрибутивности.
По аналогии с группами число элементов поля называется порядком поля. Поля, порядки которых конечны, называются конечными полями. Конечные поля имеют наибольшее значение в теории кодирования.
Отметим некоторые свойства полей, вытекающие из их определения.
1.
Для любого элемента поля 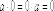 .
.
2.
Для ненулевых элементов  и
и  поля
поля  .
.
3.
Для любых элементов
и
поля 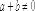 .
.
4.
Если  и
и  ,
то
,
то  .
.
33. Комплексные числа, действия над ними.
Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 =x2 и y1 = y2;
2) суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
3) произведением комплексных чисел z1 и z2 называется комплексное число
z = (x1x2 - y1y2, x1y2 + x2y1);
4)
множество комплексных чисел 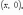
 ,
отождествляется с множеством действительных
чисел R.
,
отождествляется с множеством действительных
чисел R.
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 +z = z1, откуда находим z = z1 - z2 = (x1 - x2, y1 - y2).
Частным комплексных
чисел z1 и z2 называется
комплексное число z такое,
что 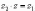 .
Отсюда находим
.
Отсюда находим
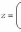


Комплексное
число (0, 1) обозначается символом i =
(0, 1). Тогда 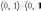
 ,
т. е. i2 =
-1. Произвольное комплексное число z можно
записать в виде
,
т. е. i2 =
-1. Произвольное комплексное число z можно
записать в виде
z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Эта запись называется алгебраической формой комплексного числа.
34. Тригонометрическая форма записи комплексных чисел.
Та
запись комплексного числа, которую мы
использовали до сих пор,
называется алгебраической
формой записи комплексного числа.
Часто бывает удобна немного другая
форма записи комплексного числа.
Пусть 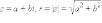 и
φ = arg z.
Тогда по определению аргумента имеем:
и
φ = arg z.
Тогда по определению аргумента имеем:
|
Отсюда получается
z = a + bi = r(cos φ + i sin φ). |
Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
35. показательная форма записи комплексного числа. (Связь между показательной и тригонометрической формой записи)
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой
|
|
которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа.
Пусть
комплексное число  в
тригонометрической форме имеет вид
в
тригонометрической форме имеет вид  .
На основании формулы Эйлера выражение
в скобках можно заменить на показательное
выражение. В результате получим
.
На основании формулы Эйлера выражение
в скобках можно заменить на показательное
выражение. В результате получим
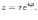
Эта
запись называется показательной
формой комплексного
числа. Так же, как и в тригонометрической
форме, здесь  ,
,  .
.
36. Кольцо многочленов. Вопросы делимости в кольце многочленов, корни многочленов.
37. Определение линейного пространства. Примеры.
Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём:
x + y = y + x − сложение коммутативно;
x + (y + z) = (x + y) + z − сложение ассоциативно;
x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);
x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0 для любого x из L).
2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элементα·x, называемый произведением α и x, причём:
α·(β·x) = (α·β)·x − умножение на число ассоциативно: ;
1·x = x − для любого элемента x из L.
3. Операции сложения и умножения на число связаны соотношениями:
α·(x + y) = α·x + α·y − умножение на число дистрибутивно относительно сложения элементов;
(α + β)·x = α·x + β·x − умножение на вектор дистрибутивно относительно сложения чисел.
Примером линейного пространства, является пространство геометрических радиусов-векторов на плоскости L = R2 = { x = x1·i + x2·j}:
x = x1·i + x2· j, y = y1·i + y2· j,
x + y = (x1+ y1)·i + ( x2+ y2)· j, α·x = (αx1)·i + (αx2)· j,
0 = 0·i + 0· j, −x = (−x1)·i +(−x2)· j.
38. Линейная зависимость векторов.
Определение
Система векторов ![]() называется линейно
зависимой,
если существует такой набор коэффициентов
называется линейно
зависимой,
если существует такой набор коэффициентов ![]() ,
из которых хотя бы один отличен от нуля,
что
,
из которых хотя бы один отличен от нуля,
что ![]() .
.
Система векторов, которая не является линейно зависимой, называется линейно независимой. Но последнее определение лучше сформулировать по другому.
Определение
Система векторов
называется линейно
независимой,
если равенство
возможно только при ![]() .
.
39. Базисы и размерность линейного пространства.
Размерность. Определение. Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью.
Будем обозначать n –мерное линейное пространство Xn , где n = dimXn — размерность пространства Xn .
Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.
Базис.
Определение. Упорядоченная система векторов e1, e2, … , en X называется базисом в X , если
система векторов e1, e2, … , en линейно независима;
любой вектор x пространства X может быть представлен в виде
x = ξ1e1 + ξ2e2 + … + ξnen.
(1)
Выражение (1) называется разложением вектора x по базису e1, e2, … , en .
Коэффициенты ξ1, ξ2, … , ξn в разложении векторапо данному базису определяются однозначно.
40. Комплексные числа, основные понятия, определения.
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
a = c и b = d.
Суммой двух комплексных чисел a + ib и c + id называется комплексное число
a + c + i(b + d).
Произведением двух комплексных чисел a + ib и c + id называется комплексное число
ac – bd + i(ad + bc). |
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
|
|
|
Следовательно,
комплексные числа вида a + i · 0 естественно
отождествляются с действительными
числами. Из-за этого комплексные числа
такого вида и называют просто
действительными. Итак, множество
действительных чисел содержится в
множестве комплексных чисел. Множество
комплексных чисел обозначается 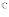 .
Мы установили, что
.
Мы установили, что  ,
а именно
,
а именно 

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
|
Таким
образом:
|
|
С
учётом этого замечательного соотношения
легко получаются формулы сложения и
умножения для комплексных чисел. Нет
нужды запоминать сложную формулу для
произведения комплексных чисел – если
на комплексные числа смотреть как
на многочлены с
учётом равенства  ,то
и перемножать эти числа можно как
многочлены. В самом деле,
,то
и перемножать эти числа можно как
многочлены. В самом деле,
|
|
то есть как раз получается нужная формула.