2Интегральное исчисление функции одной переменной
2.1Неопределенный интеграл
Определение 16 (первообразная). Функция F(x) называется первообразной функцией для функции f(x) на множестве X R, если в каждой точке этого множества F'(x) = f(x).
Например, функция F(x) = x2/2 является первообразной для функции f(x) = x, так как (x2/2)' = x. Очевидно, что если F(x) - первообразная функция для функции f(x) на множестве X, то функция F(x)+C, где C - некоторая постоянная, также является первообразной для функции f(x), x X, так как (F(x)+C)' = F'(x) = f(x). Геометрически это означает, что если найдена одна кривая y = F(x), являющаяся первообразной, то, сдвигая ее вдоль оси ординат, мы снова получим кривые, удовлетворяющие условию (F(x)+C)' = f(x).
Справедлива
Теорема 14. Если F1(x), F2(x) - первообразные для функции f(x) на некотором множестве X, то найдется такое число C, что справедливо равенство F2(x) = F1(x)+C.
Доказательство. Так как (F2(x)-F1(x))' = F'2(x)-F'1(x) = f(x)-f(x) = 0, x X, то F2(x)-F1(x) = C, то есть F2(x) = F1(x)+C.
Определение 17 (неопределенный интеграл). Совокупность всех первообразных функций для функции f(x), определенных на множестве X, называется неопределенным интегралом от функции f(x) на множестве X и обозначается
![]() f(x)dx.
f(x)dx.
Если F(x) - некоторая первообразная для f(x), то пишут
f(x)dx = F(x)+C.
2.2Основные свойства неопределенного интеграла
dF(x) = F(x)+C. Справедливость этого равенства следует из очевидной цепочки равенств
dF(x) = F'(x)dx = f(x)dx = F(x)+C.
d f(x)dx = f(x)dx. Данная формула следует из равенства
d f(x)dx = d(F(x)+C) = dF(x) = F'(x)dx = f(x)dx.
Если функции f1(x), f2(x) имеют первообразные, то функция f1(x)+f2(x) тоже имеет первообразную, причем
(f1(x)+f2 (x))dx = f1(x)dx+ f2(x)dx.
Если функция f(x) имеет первообразную и k– постоянная, то и функция kf(x) также имеет первообразную, причем при k 0 справедливо равенство
kf(x)dx = k f(x)dx.
Заметим, что свойства 3 и 4 следуют из свойств производной.
2.3Таблица интегралов
Ранее
была указана таблица производных от
основных элементарных функций (см. 1.6).
Приведем таблицу основных интегралов.
Справедливость ниже указанных формул
легко проверить дифференцированием.
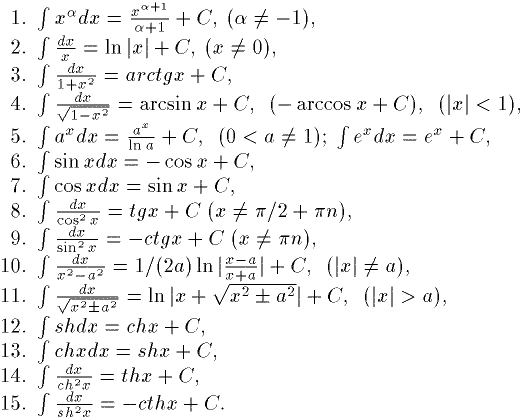
26.
Табличное интегрирование (непосредственное интегрирование) называется интегрирование , заключающиеся в прямом применении свойств неопределенного интеграла и формул из таблицы основных интегралов.
Замена переменной
 ,t=f(x)
,t=f(x)Интегрирование по частям называется нахождение интеграла по формуле
![]()
Где u , v –непрерывно дифференцированные функции.
Доказательство:
(u*v)’=u’v+v’u
![]()
Uv= ![]()
![]()
27.
Определенным интегралом от функции
f(x) на
интервале [ a,b
]( в пределах от а до b )
называется предел интегральной суммы
при условии, что длина наибольшего из
частичных интегралов ( max
![]() )
стремится к нулю, если этот предел
существует и не зависит от способа
разбиения интеграла [ a,b
]на частичные и от выбора точек
)
стремится к нулю, если этот предел
существует и не зависит от способа
разбиения интеграла [ a,b
]на частичные и от выбора точек ![]() .
Для определенного интеграла используется
обозначение
.
Для определенного интеграла используется
обозначение ![]() .
.
=![]()
Если существует
,
то о функции ![]() говорят, что она интегрируема на
интервале [ a,b
]. Числа a и b
называются соответственно нижним и
верхним пределами интегрирования.
говорят, что она интегрируема на
интервале [ a,b
]. Числа a и b
называются соответственно нижним и
верхним пределами интегрирования.
 Если f(x)
Если f(x)
![]() 0
на [ a,b ], то
определенный интеграл
геометрически представляет собой
площадь криволинейной трапеции –
фигуры, ограниченной линиями y=f(x),
x=a, x=b,
y=0
0
на [ a,b ], то
определенный интеграл
геометрически представляет собой
площадь криволинейной трапеции –
фигуры, ограниченной линиями y=f(x),
x=a, x=b,
y=0
Основные свойства определенного интеграла
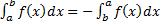
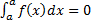
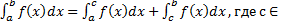 [
a, b ]
[
a, b ]
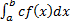 =c
=c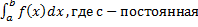
 ≤
M(b-a), если
m ≤ f(x) ≤ M при
x
≤
M(b-a), если
m ≤ f(x) ≤ M при
x  [ a, b ]
[ a, b ]
28 .
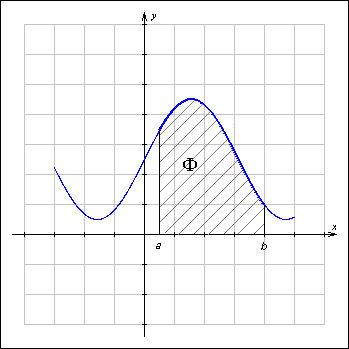
Определенный интеграл с переменным верхним пределом
Рассмотрим функцию y = f(x), интегрируемую на отрезке [а, b]. Если х на промежутке [a, b], то функция f(x) интегрируема также на любом отрезке [а, х]. Предположим, что х меняется на отрезке [а, b], тогда на этом отрезке определена функция
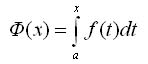
(Переменную интегрирования обозначили буквой t, переменный верхний предел - буквой х).
Теорема 1. Если функция у = f(x) интегрируема на отрезке [а, b], то функция Ф(х) непрерывна на этом отрезке.
Теорема 2. Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела. т.е.
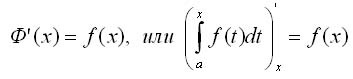
Следствие 1. Если функция f(x) непрерывна на отрезке [а, b], то при любом х
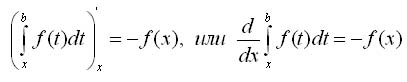
Следствие 2. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции.
Другими словами, для любой непрерывной функции существует первообразная.
Эти функции не являются элементарными; первообразные указанных подынтегральных функций не выражаются через элементарные функции.
Все приведенные функции хорошо изучены, для них составлены таблицы значений, эти функции находят широкое применение.
Связь между определенными и неопределенными интегралами выражает следующая теорема Ньютона - Лейбница, называемая основной теоремой интегрального исчисления.
Теорема 3. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной для верхнего и нижнего предела интегрирования:
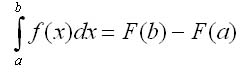
где F'(x)=f{x).
Эта формула называется формулой Ньютона - Лейбница; ее можно переписать в виде
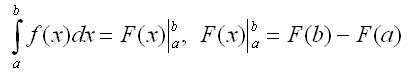
левая часть второй формулы читается так: «двойная подстановка от а до b для функции F(x).
29
При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА. Пусть функция φ(t)
имеет непрерывную производную на
отрезке [α,β], а=φ(α), в=φ(β) и функция f(х)
непрерывна в каждой точке х вида х=φ(t),
где t![]() [α,β].
[α,β].
Тогда справедливо следующее равенство:
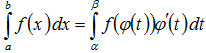
Эта формула носит название формулы замены переменной в определенном интеграле.
2.Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [ a , b ], то справедлива формула интегрирования по частям:
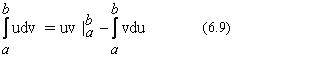
На отрезке [ a , b ] имеет место равенство (uv) /=u /v + v /u . Следовательно, функция uv есть первообразная для непрерывной функции u /v + v /u . Тогда по формуле Ньютона- Лейбница имеем
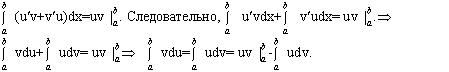
30.
Геометрический смысл определенного интеграла
Пусть f(x), заданная на a,b, непрерывна и нужно определить площадь, ограниченную кривой y = f(x) и прямыми х = а, х = b, y = 0.

Рис. 4.1
Рис. 4.2 |
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Устремим n , xi 0. Возьмем
![]() .
.
![]() .
.
Но тогда
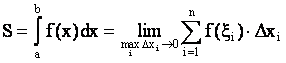 .
.
Таким образом, определенный интеграл от непрерывной неотрицательной функции при a b равен площади соответствующей криволинейной трапеции.
Площадь плоских фигур
Рассмотрим приложения определенного интеграла для вычисления площадей некоторых плоских областей.
Пусть требуется определить S - площадь криволинейной трапеции, ограниченной графиком функции y = f(x), отрезком a x b и x = a, x = b на основании геометрического смысла определенного интеграла

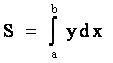 , (6.1)
, (6.1)
где y = f(х).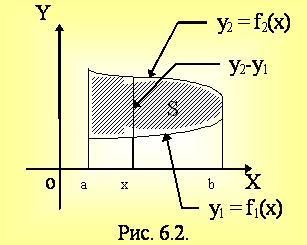
Пусть y1 = f1(x), y2 = f2(x) (y2 y1), x = a, x = b. f1(x), f2(x) 0 приx[a,b].
Тогда  .
.
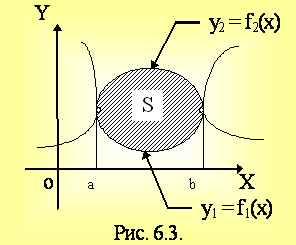
Если f1(x) = y1, f2(x) = y2
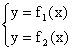 ;
; ![]() -
решение системы. Тогда так же
имеем
-
решение системы. Тогда так же
имеем
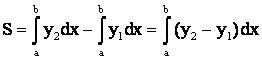 . (6.2)
. (6.2)
32.
Первый замечательный предел
Второй замечательный предел |
33.
Теорема 1 (дифференцирование сложной функции). Пусть функция x = (t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = (t). Тогда сложная функция y = f((t)) дифференцируема в точке t, причем справедлива формула
(f((t)))' = f'(x)'(t). |
(3) |
Доказательство. Зададим x = (t) отличное от нуля приращение t. Этому приращению отвечает приращение x = (t+ t)- (t) функции x = (t). Приращению x отвечает приращение y = f(x+ x)-f(x). Так как функция y = f(x)дифференцируема, то ее приращение y представимо в виде (1):
y =f'(x) x + ( x) x,
где lim x 0 ( x ) = 0. Поделив данное выражение на t 0, будем иметь:
y/ t=f'(x) x/ t+ ( x) x/ t.
Из дифференцируемости функции x = (t) в точке t вытекает, что
lim t 0 x/ t = '(t).
Отметим, что из дифференцируемости функции x = (t) следует, что x 0 при t 0. Следовательно, lim t 0 ( x) =0. Таким образом, получим необходимую формулу (3).
Теорема 2 (производная обратной функции). Пусть функция y = f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x. Пусть, кроме того, эта функция дифференцируема в точке x и f'(x)0. Тогда в некоторой окрестности соответствующей точки y = f(x) определена обратная функция x = f-1(y), причем обратная функция дифференцируема в точке x = f-1(y) и для ее производной справедлива формула
(f-1(y))' = 1/f'(x).
Доказательство. Так как функция y = f(x) строго монотонна и непрерывна в некоторой окрестности точки x, то существует обратная функция x = f-1(y), которая является строго монотонной и непрерывной в некоторой окрестности точки y = f(x).
Пусть y 0 приращение для y, а x - соответствующее приращение обратной функции x = f-1(y). Тогда справедливо равенство
x/ y = 1/( y/ x).
Переходя к пределу в последнем равенстве при y 0 и учитывая, что в силу непрерывности обратной функции x 0, получим
lim y 0 x/ y = 1/ (lim x 0 y/ x).
То есть, x'(y) = 1/y'(x).
?.
Для нахождения производной
от функции![]() в
заданной точке
в
заданной точке ![]() по
направлению вектора
по
направлению вектора ![]() используют
формулу:
используют
формулу: 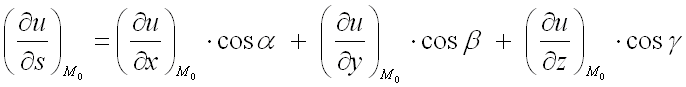 ,
где
,
где ![]() –
направляющие косинусы вектора
,
которые вычисляются по формулам:
–
направляющие косинусы вектора
,
которые вычисляются по формулам:
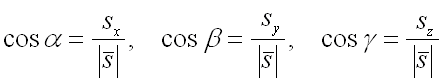 .
.
Пусть в каждой точке
некоторой области ![]() задана
функция
.
Вектор,
проекциями которого на оси координат
являются значения частных производных
этой функции в соответствующей точке,
называется градиентом
функции
и
обозначается
задана
функция
.
Вектор,
проекциями которого на оси координат
являются значения частных производных
этой функции в соответствующей точке,
называется градиентом
функции
и
обозначается ![]() или
или ![]() (читается
«набла у»):
(читается
«набла у»): 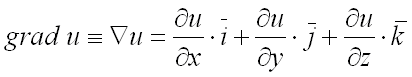 .
.
При этом говорят, что в области определено векторное поле градиентов.
Для нахождения градиента
функции
в
заданной точке
используют
формулу:
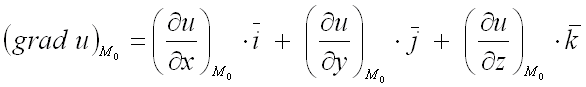 .
.
Свойства градиента
1. Производная
в данной точке по направлению
вектора ![]() имеет
наибольшее значение, если направление
вектора
совпадает
с направлением градиента. Это наибольшее
значение производной равно
имеет
наибольшее значение, если направление
вектора
совпадает
с направлением градиента. Это наибольшее
значение производной равно ![]() .
.
2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.
Пусть задана функция f(x,
y). Тогда каждая из
ее частных
производных(если
они, конечно, существуют) ![]() и
и ![]() ,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная
,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная 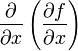 обозначается
через
обозначается
через ![]() или
или ![]() ,
а
,
а 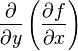 через
через ![]() или
или ![]() .
Таким образом,
.
Таким образом,
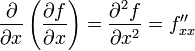 ,
, 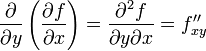
и, аналогично,
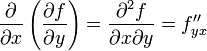 ,
, 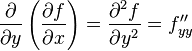 .
.
Производные ![]() и
и ![]() называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:
называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка: ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.


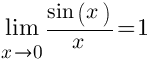 Следствия
Следствия
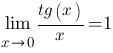
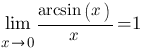

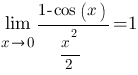
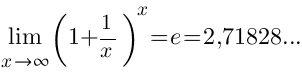 При
решении примеров полезно иметь в виду
следующие равенства:
При
решении примеров полезно иметь в виду
следующие равенства: