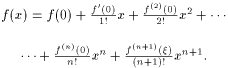1.1Производные и дифференциалы высших порядков

Предположим, что функция f'(x) является дифференцируемой в некоторой точке x интервала (a,b), то есть имеет в этой точке производную. Тогда данную производную называют второй произвоьдной и обозначают f⁽²⁾(x), f''(x) или y⁽²⁾, y''(x). Аналогично можно ввести понятие второй , третьей и т. д. производных. По индукции можно ввести понятие n- ой производной:

y(n) = (y(n-1))'.

(6)

Функцию, имеющую на некотором множестве конечную производную порядка n,называют n раз дифференцируемой на этом множестве. Методика нахождения производных высших порядков предполагает умение находить производные первого порядка, о чем говорит формула (6).

Если u(x), v(x) две дифференцируемые функции, то для нахождения производной их произведения справедлива формула Лейбница

(u(x)v(x))⁽ⁿ⁾ = u(n)v+nu(n-1)v'+(n(n-1)/2)u(n-2)v''+...+ uv(n) =

= _{k =} 0ⁿC_n^ku(n-k)v(k),

где

C_n^k = (n(n-1)(n-2)...(n-k+1))/k!, u(0) = u, v(0) = v.

Данная формула Лейбница особенно эффективна в случае, когда одна из перемножаемых функций имеет конечное число отличных от нуля производных и легко вычислить производные другой функции.

Пример 9. Пусть y = e^x(x²-1). Найти y⁽¹⁰⁾. Положим u(x) = e^x, v(x) = (x²-1). Согласно формуле Лейбница

y(10) = (e^x)⁽²⁵⁾(x2-1)+10(e^x)⁽⁹⁾(x2-1)'+(10· 9/2) (e^x)⁽⁸⁾(x2-1)'',

так как следующие слагаемые равны нулю. Поэтому

y(10) = e^x(x2-1)+10e^x2x+(10· 9/2)e^x (2) = e^x(x2+20x+89)

Рассмотрим выражение для первого дифференциала

dy = f'(x)dx.

Пусть функция, стоящая в правой части, является дифференцируемой функцией в данной точке x. Для этого достаточно, чтобы y = f(x), была дифференцируема два раза в данной точке x, а аргумент либо является независимой переменной, либо представляет собой дважды дифференцируемую функцию.

Теорема 8 (теорема Тейлора). Пусть функция f(x) имеет в точке x = a и некоторой ее окрестности производные порядка n+1. Тогда между точками a и x a найдется такая точка  , что справедлива следующая формула:

(10)

Формула (10) называется формулой Тейлора, а выражение

представляет остаточный член в форме Лагранжа. Заметим, что если функцияf(n+1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a)ⁿ. Таким образом, остаточный член можно записать в виде

R_n+1(x) = o((x-a)ⁿ) при x a.

Данная форма записи остаточного члена называется формой Пеано.

Формулой Маклорена называется формула Тейлора при a = 0:

(11)

Остаточный член в форме Пеано для формулы Маклорена имеет вид

R_n+1 = o(xⁿ) при x 0.

Приведем разложения некоторых элементарных функций по формуле Маклорена

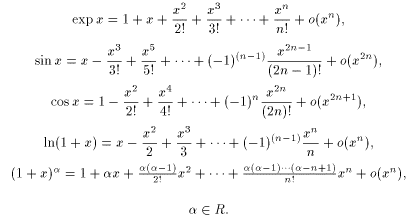
16.

Возрастание и убывание фунции. Экстремумы функции.

Определение возрастающей функции.

Функция y = f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.

Функция y = f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Достаточные признаки возрастания и убывания функции:

1) если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

2)если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Чтобы определить промежутки возрастания и убывания функции необходимо:

1)найти область определения функции;

2)найти производную функции;

3)решить неравенства и на области определения;

4)к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Достаточное условие: пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.

17.

Выпуклость графика функции. Точки перегиба

Непрерывная на отрезке [ a ; b ] функция f ( x ) называется выпуклой вверх на этом отрезке, если для любых точек x 1 и x 2 отрезка [ a ; b ] секущая AB проходит под графиком функции f ( x ), то функция f выпукла вверх.

Аналогично определяется функция, выпуклая вниз.

Дважды дифференцируемая на [ a ; b ] функция f ( x ) выпукла вверх, если для любого

Дважды дифференцируемая на [ a ; b ] функция f ( x ) выпукла вниз, если для любого

Так, вторая производная функции равна откуда следует, что квадратичная функция выпукла вниз на всей области определения.

Пусть функция f ( x ) непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда точка называется точкой перегиба функции f , если в этой точке изменяется направление ее выпуклости.

Перегиб – смена выпуклости одной на другую.

Необходимое условие наличия точки перегиба. Если – точка перегиба функции f ( x ), и функция f ( x ) имеет вторую производную, непрерывную в этой точке, то

18.

Асимптотой кривой y=f(x) называет ся прямая, к которой неограниченно приближается точка, движущаяся по кривой при неограниченном удалении ее от начала координат. Асимптоты бывают вертикальные ( уравнение такой асимптоты х=а) и наклонные ( уравнение наклонной асимптоты у=кх+в)

Для того, чтобы прямая х=а была вертикальной асимптотой необходимо и достаточно, чтобы выполнялось хотя бы одно из условий:

т.е. точка х=а должна быть точкой разрыва второго рода функции у=f(x).

Прямая у=кх+в будет наклонной асимптотой при , если существуют конечные пределы и Если область определения функции у=f(x) конечный интервал, то наклонных асимптот нет.

19

Определение. Если каждой паре (х,у) значений двух независимых переменных величин х и у из некоторой области их изменения DϵR2 соответствует определенное значение величины z , то говорят, что есть функция двух независимых переменных x и y, определенная в области D и обозначают: z=f(x,y) . Понятие придела функции двух переменных. Пусть ф-ция z=f(M) определена в некоторой области D, а M0 – внутренняя или граничная точка этой области. Число b называется приделом функции z=f(M) в точке M0, если для любой последовательности точек {Mn}(Mn≠M0, MnϵD), сходится к точке М0, соответствуящая последовательность значений функции {f(Mn)} сходится к b.

20.

Частной производной функции Z=f(x,y) по независимой переменной х называется предел вычисленный при фиксированном ( постоянном) у. Частную производную по х обозначают одним из следующих символов:

Частная производная по у обозначается : ; и определяется аналогично: :

Аналогично вводятся понятия и обозначения частных производных функций большего числа переменных. Так, в случае функции трех переменных u= f(x,y,z): ; .

Из определения частных производных следует, что частная производная функции по любой переменной есть обыкновенная производная функция по этой переменной, вычисленная в предположении, что остальные переменные ( т.е. постоянные ). Поэтому, частные производные вычисляются по формулам и правилам вычисления производных функций одной переменной.

Полным дифференциалом dz дифференцируемой функции z= f(x,y) называется главная часть полного приращения линейная относительно dx= dx+ dy.

Аналогично определяется полный дифференциал дифференцируемой функции любого ( конечного ) числа переменных. Так, если u=f (x, y, z), то du= При достаточно малых приращениях ( дифференциалах ) аргументов дифференцируемой функции справедливо приближенное равенство: