
1.
Последовательностью называется числовая функция, определенная на множестве натуральных чисел.
Определение.Число ![]() называется пределом последовательности
называется пределом последовательности ![]() ,
если для любого положительного
числа
,
если для любого положительного
числа ![]() найдется
член последовательности такой, что все
члены последовательности
,
следующие за ним, отстоят от
меньше,
чем на
.
найдется
член последовательности такой, что все
члены последовательности
,
следующие за ним, отстоят от
меньше,
чем на
.
Определение. Число называется пределом последовательности , если в любом открытом промежутке, содержащем число , содержатся все члены последовательности , начиная с некоторого.
Теорема (о единственности предела).
Если
—
предел последовательности ![]() и
и ![]() —
предел последовательности
,
то
—
предел последовательности
,
то ![]() .
.
Доказательство. Предположим,
что ![]() .
Возьмем
.
Возьмем ![]() .
Найдется такой номер
.
Найдется такой номер ![]() ,
что
,
что ![]()
![]()
также существует ![]()
![]()
Возьмем ![]() ,
которое больше
и
,
которое больше
и ![]() .
Тогда
.
Тогда
![]()
Обозначение. есть предел :
![]() ,
,
![]() —
стремится
(сходится) к
,
—
стремится
(сходится) к
,
![]()
Определение. Последовательность, имеющая предел, называется сходящейся.
Определение. Последовательность
называется строго
возрастающей (возрастающей)
[строго
убывающей] ![]() убывающей
убывающей![]() ,
если каждый ее член, начиная со второго,
больше (не меньше) [меньше]
не
больше
предыдущего
члена.
,
если каждый ее член, начиная со второго,
больше (не меньше) [меньше]
не
больше
предыдущего
члена.
Последовательности (строго) возрастающая и (строго) убывающая называются (строго) монотонными.
Определение. Последовательность
называется ограниченной,
если существует ![]() .
.
Геометрическая интерпретация предела переменной
Из определения предела следует: если переменная xn имеет пределом число a, то это значит, что как бы мало не было любое наперед заданное положительное число e, всегда можно найти такое значение xN, что все последующие ее значения будут удовлетворять неравенству
|xn - a| < e при n і N (1)
Легко видеть, что неравенство (1) равносильно следующим двум неравенствам:
-e < xn - a < e (2)
В самом деле, если xn - a > 0, то из неравенства xn - a < e имеем |xn - a| < e. Если же xn - a < 0, то из неравенства -e < xn - a имеем|xn - a| < e. Прибавляя a ко всем частям неравенств (2), получаем два других неравенства, равносильных неравенству (1):
2.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Основные свойства:
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если
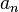 —
бесконечно малая последовательность,
сохраняющая знак, то
—
бесконечно малая последовательность,
сохраняющая знак, то 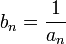 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Эквивалентные бесконечно малые -
Если ![]() ,
то бесконечно малые
величины
,
то бесконечно малые
величины ![]() и
и ![]() называются эквивалентными (
называются эквивалентными (![]() ).
).
4.
Для нахождения пределов на практике пользуются следующими теоремами.
Теорема
1. Если
существуют пределы
![]()
![]() (6.4)
(6.4)
![]() (6.5)
(6.5)
![]() (6.6)
(6.6)
Замечание. Выражения вида 0/0, /, 0 , - являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”.
Теорема
2.
![]()
![]() (6.7)
(6.7)
т.е.
можно переходить к пределу в основании
степени при постоянном показателе, в
частности,
![]() ;
;
![]() (6.8)
(6.8)
![]() (6.9)
(6.9)
Теорема
3.
![]()
![]() (6.10)
(6.10)
![]() (6.11)
(6.11)
где e 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первого и второго замечательного пределов.
Теорема 1. Если последовательности
{
![]() } и {
} и {
![]() } имеют пределы, то
} имеют пределы, то
![]() .
.
Доказательство.
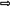
![]() , 1
>0 N1n
(n
N1
, 1
>0 N1n
(n
N1
![]() )
)
![]() , 2
>0 N2n
(n
N2
, 2
>0 N2n
(n
N2
![]() )
)
Рассмотрим последовательность
![]() .
.
![]() .
.
3 >0 N3n
(n
N3
![]() ) ,
) ,
![]() , при этом
, при этом
N3 = max{N1, N2}, что и требовалось доказать.
Теорема 2. (Необходимые и достаточные условия существования предела последовательности):
Необходимость. Если
![]() , то
, то
![]() ,
где
,
где
![]() - б.м. последовательность.
- б.м. последовательность.
Достаточность. Если , где - б.м. последовательность, то
.
5.
Предел
функции по Гейне
Значение ![]() называется пределом (предельным
значением) функции
называется пределом (предельным
значением) функции ![]() в
точке
в
точке ![]() ,
если для любой последовательности точек
,
если для любой последовательности точек ![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции ![]() сходится
к
.
сходится
к
.
![]() ^
^
Предел
функции по КошиЗначение
называется пределом (предельным
значением) функции
в
точке
,
если для любого наперёд взятого
положительного числа ![]() найдётся
отвечающее ему положительное число
найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
такое,
что для всех аргументов ![]() ,
удовлетворяющих условию
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .
.
![]()
Односторонние пределы.
Число A' называется пределом слева функции f(x) в точке a:
![]()
если
|A' - f(x)| < ε при 0 < a - x < δ (ε).
Аналогично, число A" называется пределом справа функции f(x) в точке a:
![]()
если
|A" - f(x) |< ε при 0 < x - a < δ (ε).
Для существования предела функции в точке необходимо и достаточно, чтобы
f (a - 0) = f(a + 0).
Теорема 1 (необходимое и достаточное условие существования предела). Функция y = f(x)
имеет конечный предел в точке a, тогда и только тогда, когда для любого числа ε > 0 найдётся
такое δ > 0, что для всех x и x′ , удовлетворяющих неравенствам 0 < |x − a| < δ, 0 < |x′ − a| < δ, выполнено неравенство |f(x) − f(x′)| < ε.
Аналогичные условия можно сформулировать для существования конечного предела в плюс и
минус бесконечности.
Предложение 4. Если функция имеет предел в точке a и a1, a2, . . . , an, . . . — такая последовательность, что lim n→∞ an = a, то lim x→a f(x) = lim n→∞ f(an).
6.
1. Бесконечно малые и бесконечно большие функции. Эквивалентные
бесконечно малые и бесконечно большие функции и использование их на
практике
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Последовательность
называется бесконечно
малой, если ![]() .
Например, последовательность чисел
.
Например, последовательность чисел ![]() —
бесконечно малая.
—
бесконечно малая.
Функция называется бесконечно
малой в окрестности точки ![]() ,
если
,
если ![]() .
.
Функция называется бесконечно
малой на бесконечности,
если ![]() либо
либо ![]() .
.
Также бесконечно малой
является функция, представляющая собой
разность функции и её предела, то есть
если ![]() ,
то
,
то ![]() ,
, ![]() .
.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Последовательность
называется бесконечно
большой, если ![]() .
.
Функция называется бесконечно
большой в окрестности точки
,
если ![]() .
.
Функция называется бесконечно
большой на бесконечности,
если ![]() либо
либо ![]() .
.
Эквивалентные величины
Если , то бесконечно малые величины и называются эквивалентными ( ).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При ![]() справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
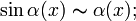

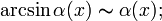

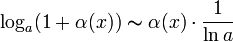 ,
где
,
где 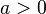 ;
;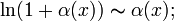
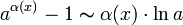 ,
где
;
,
где
;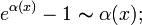
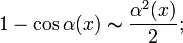
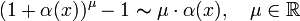 ,
поэтому используют выражение:
,
поэтому используют выражение:
![]() ,
где
.
,
где
.
7.
Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если
|
|
На практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a :
Функция f (x) определена в точке x = a;
Предел
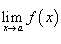 существует;
существует;Выполняется равенство
 .
.
Необходимое и достаточное
условие непрерывности функции f (x)
в точке ![]() :
f(
:
f(![]() =
f(
=
f(![]() =
f(
=
f(![]()
Для непрерывной функции бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции . т.е. если ∆x->0,то и ∆f(x)->0
F(x) непрерывна на [а;в],если она непрерывна в каждой точке этого интервала.
Точка разрыва функции-это точка в которой нарушены условия непрерывности.
Классификация точек разрыва:
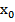 называют точкой Устранимого разрыва,
если f(
=
f(
≠
f(
называют точкой Устранимого разрыва,
если f(
=
f(
≠
f(
называют точкой разрыва 1го рода, если в этой точке у функции существуют конечные односторонние пределы , но f( ≠f( . При этом разность f( - f( называют скачком функции в точке .
называют точкой разрыва 2го рода , если в этой точке функция не имеет хотя бы одного из односторонних пределов.
8.
Похідна функції – основне поняття диференційного числення, що характеризує швидкість зміни функції.
Функцію, що має кінцеву похідну, називають диференційною.
Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на D x№ 0 получим
D y/D x = A+a(D x).
Переходя к пределу в последнем выражении при D x® 0, получим, что A=f'(x).
Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел
limD x® 0D y/D x = f'(x).
Обозначим a(D x) = D y/ D x-f'(x). Отсюда вытекает представление (1).
Пример 4. Доказать, что функция |x| не дифференцируема в точке x = 0.
Решение. Найдем приращение функции в точке x = 0 :
D y = |D x|
Поэтому
limD x® -0D y/D x = -1, limD x® +0D y/D x = 1,
следовательно, функция |x| в точке x = 0 не дифференцируема.
9.
Геометрический смысл производной
Производная функции y=f(x) в точке x=x0 равна тангенсу угла наклона касательной к графику этой функции в данной точке.
Используя этот факт, запишем уравнение касательной в точке x=x0 y — f(x0) = f`(x0)(x — x0)
Механический смысл производной
Пусть S=S(t) является функцией зависимости пути от времени. Тогда
![]()
Отсуда следует, что производная функции равняется мгновенной скорости изменения функции.
Эластичность
есть мера изменения зависимой переменной
в ответ на изменение независимой
переменной.
Пусть
y(x) -функция, характеризующая, например,
издержки производства, где x - количество
выпускаемой продукции. Тогда отношение
y(x)/x описывает средние издержки,
приходящиеся на одно изделие. Средняя
величина обозначается Ay или Af (от
английского "average".) Среднее
приращение, средний прирост, средняя
скорость изменения определяется
отношением D y/D x.
Производная
![]() выражает
предельные (маргинальные от английского
"marginal") издержки производства.
Величину Mf(x) = y' называют мгновенным
приростом или мгновенной скоростью
изменения y. Аналогично можно определить
предельную выручку, предельный доход,
предельную полезность и другие предельные
величины.
Эластичностью
функции Ex(y) называется величина
выражает
предельные (маргинальные от английского
"marginal") издержки производства.
Величину Mf(x) = y' называют мгновенным
приростом или мгновенной скоростью
изменения y. Аналогично можно определить
предельную выручку, предельный доход,
предельную полезность и другие предельные
величины.
Эластичностью
функции Ex(y) называется величина
![]() Считаем,
что y(x) эластична в точке x, если |Ex(y)|>1,
y(x) неэластична, если |Ex(y)| <1, и нейтральна,
если |Ex(y)| = 1.
Свойства
эластичности.
Эластичность -
безразмерная величина, ее значение не
зависит от того, в каких единицах измерены
аргумент и функция. Если u = Ax, v = By, то
Eu(v) = (dv/du)· u/v=(B/A)· (dy/dx)· (Ax/By) = Ex(y);
Эластичности
взаимно обратных функций - взаимно
обратные величины
Ey(x) = (dx/dy)·(y/x) =
1/Ex(y).
Эластичность функции равна
произведению независимой переменной
x на темп изменения функции Ty = (ln y)' =
y'/y, то есть
Ex(y) = xTy.
Эластичность
произведения (частного) двух функций
равна сумме (разности) эластичностей
этих функций:
Ex(uv) = Ex(u)+Ex(v), Ex(u/v) =
Ex(u)-Ex(v).
Из последнего свойства следуют
формулы
Ex(xy) = Ex(x)+Ex(y) = 1+Ex(y)
отсюда,
если Ex(y)>-1, то xy монотонно возрастает;
если Ex(y)<-1, то xy монотонно убывает.
Аналогично,
Ex(y/x) = Ex(y)-Ex(x) = Ex(y)-1
Считаем,
что y(x) эластична в точке x, если |Ex(y)|>1,
y(x) неэластична, если |Ex(y)| <1, и нейтральна,
если |Ex(y)| = 1.
Свойства
эластичности.
Эластичность -
безразмерная величина, ее значение не
зависит от того, в каких единицах измерены
аргумент и функция. Если u = Ax, v = By, то
Eu(v) = (dv/du)· u/v=(B/A)· (dy/dx)· (Ax/By) = Ex(y);
Эластичности
взаимно обратных функций - взаимно
обратные величины
Ey(x) = (dx/dy)·(y/x) =
1/Ex(y).
Эластичность функции равна
произведению независимой переменной
x на темп изменения функции Ty = (ln y)' =
y'/y, то есть
Ex(y) = xTy.
Эластичность
произведения (частного) двух функций
равна сумме (разности) эластичностей
этих функций:
Ex(uv) = Ex(u)+Ex(v), Ex(u/v) =
Ex(u)-Ex(v).
Из последнего свойства следуют
формулы
Ex(xy) = Ex(x)+Ex(y) = 1+Ex(y)
отсюда,
если Ex(y)>-1, то xy монотонно возрастает;
если Ex(y)<-1, то xy монотонно убывает.
Аналогично,
Ex(y/x) = Ex(y)-Ex(x) = Ex(y)-1
10.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
![]() .
.
Доказательство. Проведем
доказательство для двух слагаемых, так
как для любого числа слагаемых оно
проводится так же.
Пусть ![]() .Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
.Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + c есть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
![]() .
.
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
![]() .
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть
величина постоянная. Функция bβ
+ c α + αβ на основании
свойств бесконечно малых функций есть
величина бесконечно малая. Поэтому ![]() .
.
Следствие 1. Постоянный
множитель можно выносить за знак
предела:![]() .
.
Следствие 2. Предел
степени равен степени предела:![]() .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
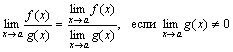 .
.
Доказательство. Пусть ![]() .
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α, β –
бесконечно малые. Рассмотрим частное
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α, β –
бесконечно малые. Рассмотрим частное
![]() .
.
Дробь ![]() является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
11.
Дифференцирование неявной функции.
а) Пусть дано уравнение, связывающее две переменные х и у. Если все члены этого уравнения перенести в левую часть, то оно будет иметь вид
![]() (1)
(1)
Уравнение (1) вообще говоря, определяет
одну или несколько функций
![]() .
Например, уравнение
.
Например, уравнение
![]() определяет одну функцию
определяет одну функцию
![]() ,
а уравнение
,
а уравнение
![]() определяет две функции
определяет две функции
![]() и
и
![]() .
.
Если в рассмотренные уравнения вместо у подставить найденные функции, то они обратятся в тождества.
Определение: Всякая непрерывная
функция
,
обращающая уравнение
в тождество, называется неявной функцией,
определяемой уравнением
![]() .
.
Не всякое уравнение
определяет неявную функцию. Так уравнение
![]() не удовлетворяет ни одной паре
действительных чисел
не удовлетворяет ни одной паре
действительных чисел
![]() и, следовательно, не определяет неявную
функцию. Сформулируем условия, при
которых уравнение
определяет неявную функцию
и, следовательно, не определяет неявную
функцию. Сформулируем условия, при
которых уравнение
определяет неявную функцию
![]() .
.
Пусть дано уравнение (1)
б) Теорема существования неявной функции.
Если функция
![]() и её частные производные
и её частные производные
![]() и
и
![]() определены и непрерывны в некоторой
окрестности точки
определены и непрерывны в некоторой
окрестности точки
![]() и при этом
и при этом
![]() ,
а
,
а
![]() ,
то уравнение
определяет в этой окрестности точки
,
то уравнение
определяет в этой окрестности точки
![]() единственную неявную функцию
,
непрерывную и дифференцируемую в
некотором интервале, содержащем точку
единственную неявную функцию
,
непрерывную и дифференцируемую в
некотором интервале, содержащем точку
![]() ,
причём
,
причём
![]() .
.
Геометрически это означает, что в окрестности точки кривая представляет собой график непрерывной и дифференцируемой функции .
в) Производная неявной функции.
Пусть левая часть уравнения
удовлетворяет условиям, указанным в
теореме, тогда это уравнение определяет
неявную функцию
,
для которой в окрестности точки
![]() имеет место тождество относительно х:
имеет место тождество относительно х:
![]() .
Тогда
.
Тогда
![]() ,
при любом х из окрестности х0.
,
при любом х из окрестности х0.
По правилу дифференцирования сложной
функции
![]()
и, значит,
![]() .
.
Отсюда
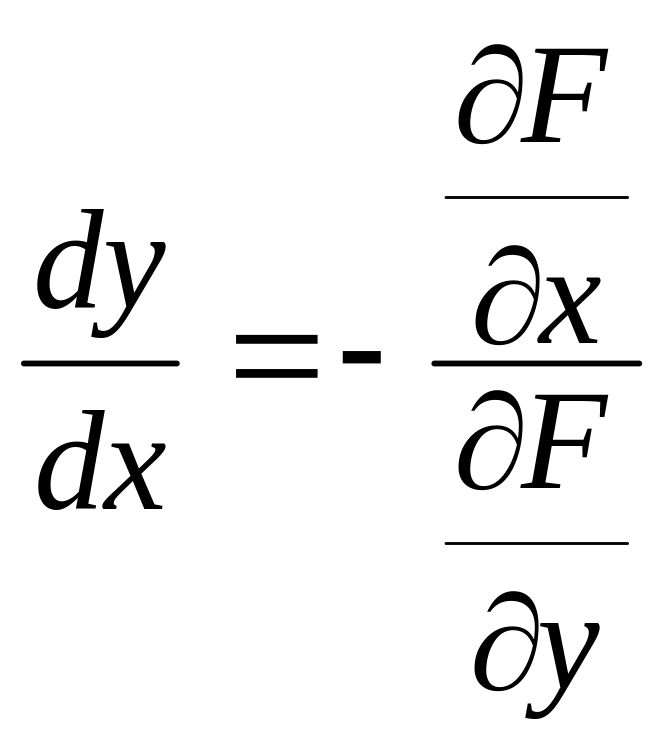 или
или
![]() (2)
(2)
По этой формуле находится производная неявной функции (одной переменной ).
Пример: х3+у3-3ху=0
Имеем
![]() х3+у3-3ху,
х3+у3-3ху,
![]() =3х2-3у
=3х2-3у
![]() =3у2-3х
=3у2-3х
![]() =
-
=
-
![]() .
.
Обобщим понятие неявно заданной функции на случай функции нескольких переменных.
Уравнение
![]() (3) определяет неявно заданную функцию
(3) определяет неявно заданную функцию
![]() ,
если эта функция непрерывна и обращает
уравнение
в тождество, т.е.
,
если эта функция непрерывна и обращает
уравнение
в тождество, т.е.
![]() (4).
(4).
Условия существования и единственности неявно заданной функции формулируются аналогично.
Найдём
![]() и
и
![]() :
:
![]() =
-
=
-
![]()
![]() =
-
=
-
![]()
Пример:
![]()
![]()
![]()
![]() 2х
2х
![]() 2у
2у
![]()
![]()
Тогда
![]() =
-
=
-
![]() ;
;
![]() =
-
=
-
![]() .
.
Дифференцирование функции заданной параметрически
Если функция у аргумента х задана
параметрическими уравнениями
![]() ,
то
,
то
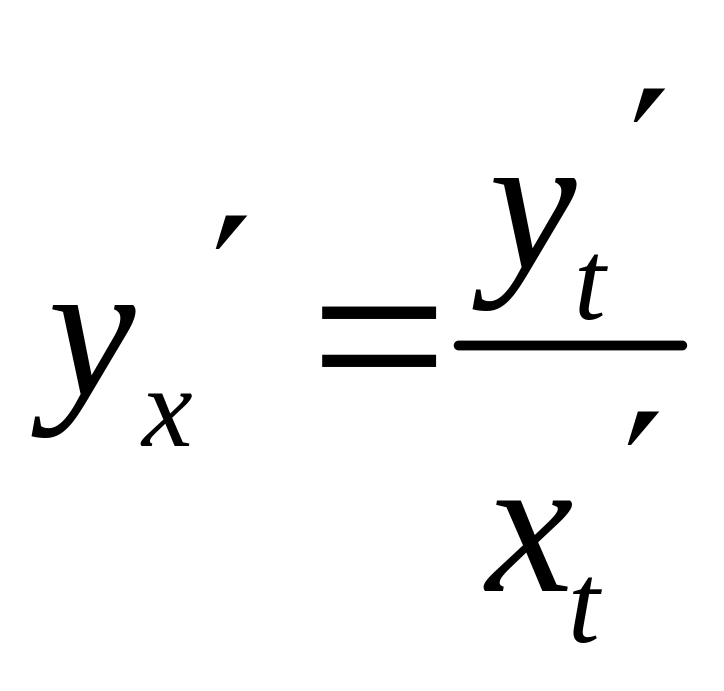 .
.
Пусть функция у от х задана параметрическими
уравнениями:
![]() .
.
Предположим, что эти функции имеют
производные и что функция
![]() имеет обратную
имеет обратную
![]() ,
которая так же имеет производную . тогда
определенную параметрическими уравнениями
функцию y=f(x)
можно рассматривать ак сложную функцию
,
которая так же имеет производную . тогда
определенную параметрическими уравнениями
функцию y=f(x)
можно рассматривать ак сложную функцию
![]() ,
t – промежуточный аргумент.
По правилу дифференцирования сложной
функции получим:
,
t – промежуточный аргумент.
По правилу дифференцирования сложной
функции получим:
![]() .
На основании теоремы о дифференцировании
обратной функции следует:
.
На основании теоремы о дифференцировании
обратной функции следует:
![]() .
После подстановки получаем :
.
После подстановки получаем :

Понятие дифференциала функции
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
![]()
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/Dх=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.
Таким образом, приращение
функции ∆у представляет собой сумму
двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся
бесконечно малыми при ∆x→0. При этом
первое слагаемое есть бесконечно малая
функция одного порядка с ∆х, так как![]() а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем ∆х:
а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем ∆х:
![]()
Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (3)
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (3), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (3) можно записать так:
dy=ƒ'(х)dх, (4)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (4) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.
<< Пример 3
Найти дифференциал функции ƒ(х)=3x2-sin(l+2x).
Решение: По формуле dy=ƒ'(х) dx находим
dy=(3х2-sin(l+2x))'dx=(6х-2cos(l+2х))dx.
<< Пример 4
Найти дифференциал функции
![]()
Вычислить dy при х=0, dx=0,1.
Решение:
![]()
Подставив х=0 и dx=0.1, получим
![]()
12.
Теорема Ферма.
Функция f(x) непрерывна на открытом интервале (a;b) в точке х0, которая принадлежит (a;b), она достигает своего max и min. Тогда если существует f `(x0), она равна 0 (f `(x0)=>0)
Следствие из теоремы Ферма:
В точке локального экстремума х0, Є (a;b) f(x0)=0, если она существует.
(которая принадлежит=Є)
13.
Теорема Ро́лля (теорема о нуле производной) утверждает, что:
Е сли
вещественная функция, непрерывная на
отрезке
сли
вещественная функция, непрерывная на
отрезке ![]() и дифференцируемая на
интервале
и дифференцируемая на
интервале ![]() ,
принимает на концах этого интервала
одинаковые значения, то на этом интервале
найдётся хотя бы одна точка, в
которой производная
функции равна
нулю.
,
принимает на концах этого интервала
одинаковые значения, то на этом интервале
найдётся хотя бы одна точка, в
которой производная
функции равна
нулю.
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
Формула
конечных приращений или теорема
Лагра́нжа о среднем значении утверждает,
что если функция ![]() непрерывна на
отрезке
идифференцируема в
интервале
,
то найдётся такая точка
непрерывна на
отрезке
идифференцируема в
интервале
,
то найдётся такая точка ![]() ,
что
,
что
![]() .
.
Геометрически это можно переформулировать так: на отрезке найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Интегральная теорема Коши — утверждение из теории функций комплексного переменного.
Для любой
функции ![]() , аналитической в
некоторой односвязной области
, аналитической в
некоторой односвязной области ![]() и
для любой замкнутой кривой
и
для любой замкнутой кривой ![]() справедливо
соотношение
справедливо
соотношение ![]()
3) Ограниченой
называется переменная Хn,
если существуеттакое число А>0, что
для всех n выполняется
условие |Xn|<A.
Если переменная Хn
имеет редел, то она ограниченная.
Если переменная Хn
не принемает нулевых значений и
l![]() ,
то переменная
,
то переменная ![]() -
ограниченная
-
ограниченная
Произведение ограниченой величині на безконечно малую есть безконечно малая величина.
31)Несобственными інтегралами называются:
1) интегралы с бесконечными пределами;
2) интегралы от неограниченных фунуций
Несобственный интеграл
от функции f(x)
в пределах от а до +![]()
определяется равенством ![]() .
.
Если этот предел существует и бесконечен, то несобственный интеграл называется сходящимся, если же предел не существует или равен бесконечности- расходящимся.
Аналогично ![]()
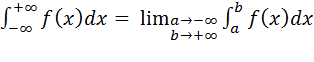 /
/
Если функция f(x)
не ограничена на интервале (a;b]
или [a;b), но
ограничена и интегрируема на любом
интервале [a+альфа;b]
или [a;b-альфа],
то по определению полагают ![]() или, соответственно,
или, соответственно, ![]() .
Если эти пределы существуют, то
несобственные интегралы называются
сходящимися, в противном случае-
расходящимися.
.
Если эти пределы существуют, то
несобственные интегралы называются
сходящимися, в противном случае-
расходящимися.
Если функция f(x)
не ограничена на [a;c)
и(c;b], где
a<c<b,
но ограничена и интегрируема на любых
интервалах [a;c;-альфа]
и [c+ B;b],
то в этом случае полагают ![]() .
.
14
Теорема Лопиталя. (Раскрытие
неопределенностей типа
![]() )
Пусть
функции f(x), g(x) определены, непрерывны
и дифференцируемы в точке x0 и
некоторой ее окрестности, причемg'(x)
0 для любого x из этой окрестности, и
пусть f(x0) = 0, g(x0) = 0 (следовательно,
f(x), g(x) – бесконечно малые при
)
Пусть
функции f(x), g(x) определены, непрерывны
и дифференцируемы в точке x0 и
некоторой ее окрестности, причемg'(x)
0 для любого x из этой окрестности, и
пусть f(x0) = 0, g(x0) = 0 (следовательно,
f(x), g(x) – бесконечно малые при![]() ).
Если
).
Если
![]()
![]() существует,
то существует
существует,
то существует
![]() и
=
.
(2.18)
Доказательство. Равенство
(2.18) называют правилом Лопиталя для
раскрытия неопределенностей типа
и
=
.
(2.18)
Доказательство. Равенство
(2.18) называют правилом Лопиталя для
раскрытия неопределенностей типа
![]() .
Дадим
значению аргумента x0 приращение
x, такое, чтобы точка
x = x0 + x
принадлежала рассматриваемой окрестности
точки x0.
Случай 1.x
> 0, тогда x >x0. Функции f(x), g(x),
рассматриваемые на отрезке [x0,
x], удовлетворяют теореме Коши, поэтому
найдется такое c (x0,
x), что выполняется равенство:
.
Дадим
значению аргумента x0 приращение
x, такое, чтобы точка
x = x0 + x
принадлежала рассматриваемой окрестности
точки x0.
Случай 1.x
> 0, тогда x >x0. Функции f(x), g(x),
рассматриваемые на отрезке [x0,
x], удовлетворяют теореме Коши, поэтому
найдется такое c (x0,
x), что выполняется равенство:
![]() =
=![]() .
Так как f(x0) = g(x0) = 0, то получим:
=
.
Заметим, что число c зависит от x, но если
,
то
.
Так как f(x0) = g(x0) = 0, то получим:
=
.
Заметим, что число c зависит от x, но если
,
то
![]() ,
так как x0 <c <x. Переходя к пределу
в последнем равенстве,
получаем:
=
=
,
так как x0 <c <x. Переходя к пределу
в последнем равенстве,
получаем:
=
=![]() =
.
Случай
2.x < 0, тогда x
<x0. Функции f(x), g(x), рассматриваемые
на отрезке
[x, x0], удовлетворяют
условиям теоремы Коши, и потому
доказательство аналогично, как в случае
1. Итак, теорема Лопиталя доказана.
Замечание
1. Теорема Лопиталя справедлива и в
том случае, когда функции f(x), g(x) не
определены в точке x0, но
f(x)
= 0 и
g(x)
= 0. В самом деле, если доопределить f (x),
g(x), положив f(x0) = g(x0) = 0, тогда
f(x), g(x) будут непрерывны в точке x0,
а потому теорема Лопиталя будет применима
к ним.
Замечание 2. Правило
Лопиталя применимо и в том случае, когда
=
.
Случай
2.x < 0, тогда x
<x0. Функции f(x), g(x), рассматриваемые
на отрезке
[x, x0], удовлетворяют
условиям теоремы Коши, и потому
доказательство аналогично, как в случае
1. Итак, теорема Лопиталя доказана.
Замечание
1. Теорема Лопиталя справедлива и в
том случае, когда функции f(x), g(x) не
определены в точке x0, но
f(x)
= 0 и
g(x)
= 0. В самом деле, если доопределить f (x),
g(x), положив f(x0) = g(x0) = 0, тогда
f(x), g(x) будут непрерывны в точке x0,
а потому теорема Лопиталя будет применима
к ним.
Замечание 2. Правило
Лопиталя применимо и в том случае, когда
![]() f(x)
= 0,
g(x)
= 0.
Теорема Лопиталя. (Раскрытие
неопределенностей типа
f(x)
= 0,
g(x)
= 0.
Теорема Лопиталя. (Раскрытие
неопределенностей типа
![]() )
Пусть
функции f(x), g(x) дифференцируемы в
окрестности точке x0, за исключением
самой точки x0, причемg'(x)
0, и пусть
)
Пусть
функции f(x), g(x) дифференцируемы в
окрестности точке x0, за исключением
самой точки x0, причемg'(x)
0, и пусть
![]() f(x)
= ,
g(x)
= . Если существует
f(x)
= ,
g(x)
= . Если существует
![]() ,
то существует
и
=
.
Доказательство
этой теоремы мы не приводим, его можно
найти в учебниках.
Отметим, что
эта теорема верна для случая, когда x,
в этом можно убедиться, повторяя
рассуждения замечания 2.
Замечание
3. Предел отношения двух функций может
существовать, в то время как предел
отношения их производных не
существует.
Замечание 4.
Если
при
x x0 (x )
является неопределенностью типа
или
,
и
,
то существует
и
=
.
Доказательство
этой теоремы мы не приводим, его можно
найти в учебниках.
Отметим, что
эта теорема верна для случая, когда x,
в этом можно убедиться, повторяя
рассуждения замечания 2.
Замечание
3. Предел отношения двух функций может
существовать, в то время как предел
отношения их производных не
существует.
Замечание 4.
Если
при
x x0 (x )
является неопределенностью типа
или
,
и
![]() (x),
g'(x) удовлетворяют условиям теоремы
Лопиталя, то
=
=
(x),
g'(x) удовлетворяют условиям теоремы
Лопиталя, то
=
=
![]() .
Таким
образом, для раскрытия неопределенностей
типа
или
иногда
приходится применять правило Лопиталя
несколько раз.
.
Таким
образом, для раскрытия неопределенностей
типа
или
иногда
приходится применять правило Лопиталя
несколько раз.
Замечание 5. Теорема Лопиталяостается верной и тогда, когда = .
15.
