4.2 Закон сохранения импульса. Центральный удар двух тел

Закон сохранения импульса: полный импульс замкнутой системы остается постоянным.Для замкнутой системы будут сохраняться и проекции импульса на координатные оси:

.

Если 0, но =0, то будет сохраняться проекция импульса системы на ось Х.Рассмотрим центральный удар двух тел. Центральным называется удар, при котором тела движутся вдоль прямой, соединяющей их центры масс. Выделяют два предельных вида такого удара: абсолютно упругий и абсолютно неупругий. Для двух тел массами m₁ и m₂ , движущихся со скоростями и вдоль оси х, проекции их скоростей на ось х после абсолютно упругого центрального удара можно найти по формулам:

; .При этом сохраняются импульс и механическая энергия системы тел.

Если удар абсолютно неупругий,то .

Тела после такого удара движутся вместе. Импульс системы тел сохраняется, а полная механическая энергия не сохраняется. Часть механической энергии переходит в энергию неупругой деформации и во внутреннюю энергию тел.

4.3 Закон сохранения момента импульса

Закон сохранения момента импульса: момент импульса замкнутой системы тел сохраняется: если .

Если результирующий момент внешних сил не равен нулю, но равна нулю его проекция на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.

5. Элементы специальной теории относительности5.1 Постулаты Эйнштейна. Преобразования ЛоренцаПервый постулат Эйнштейна: никакими физическими опытами, производимыми внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется прямолинейно и равномерно.Второй постулат Эйнштейна: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.

Рассмотрим две системы отсчета S и S (рис. 8). Систему S будем считать условно неподвижной. Система движется относительно со скоростью вдоль оси X системы . Для перехода от одной системы отсчета в другую в специальной теории относительности используются преобразования Лоренца.Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают.

Тогда:

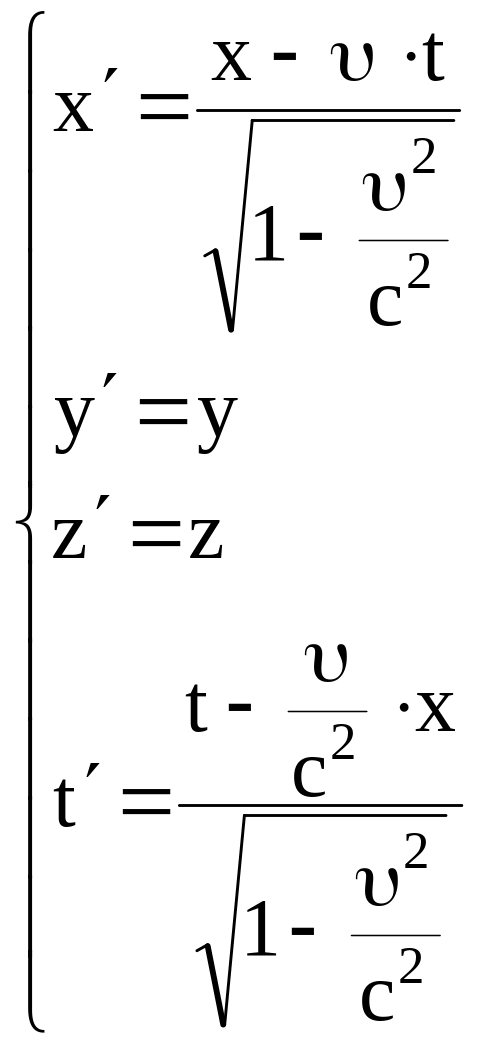
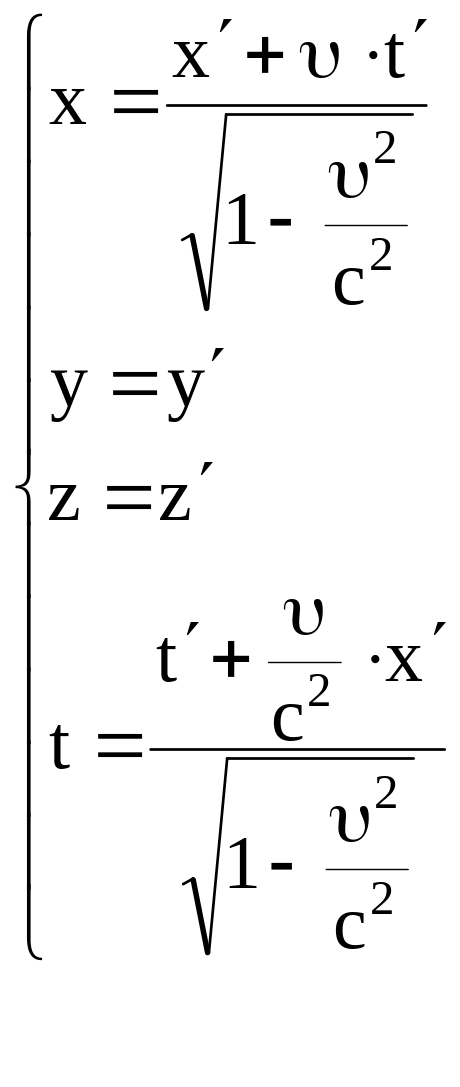
Здесь с = 310⁸ м/с – скорость света в вакууме.

5.2 Следствия из преобразований ЛоренцаРассмотрим системы и (рис. 8).Относительность промежутков времени между событиями: где – промежуток времени между событиями, произошедшими в системе отсчета ( отсчитывается по часам, находящимся в системе ); – промежуток времени между этими событиями, отсчитанный по часам, находящимся в системе .Изменение размеров движущихся тел

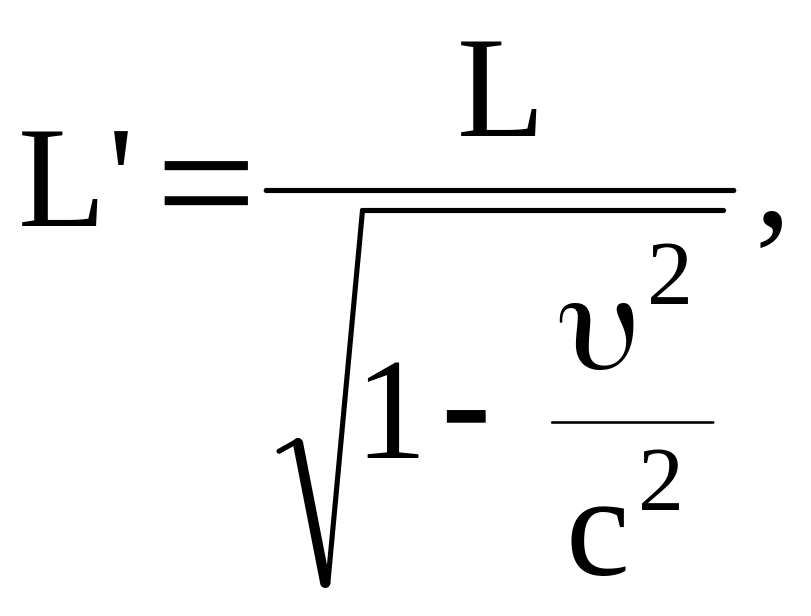где L – длина стержня, расположенного вдоль оси и покоящегося в системе S (отсчитывается в системе отсчета S); L – длина этого же стержня, измеренная в системе отсчета .

Релятивистский закон сложения скоростей:

Пусть некоторое тело движется вдоль оси x в системе отсчета со скоростью относительно последней. Найдем проекцию скорости этого тела в системе отсчета на ось х этой системы: