
- •1.1 Кинематические характеристики движения материальной точки
- •1.2 Тангенциальная и нормальная составляющие ускорения
- •Третий закон Ньютона: силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению:
- •3.3 Кинетическая энергия при поступательном и вращательном движениях
- •Принцип работы
- •Закон Гука в простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:
- •Получение
- •4.2 Закон сохранения импульса. Центральный удар двух тел
- •4.3 Закон сохранения момента импульса
- •5.3 Релятивистские масса и импульс. Взаимосвязь массы и энергии
- •Методы определения вязкости
- •II. Основы молекулярной физики и термодинамики
- •1.2 Уравнение состояния Ван-дер-Ваальса
- •1.4 Статистические распределения
- •1.4.2 Распределение Больцмана
- •1.5 Среднее число столкновений и средняя длина свободного пробега молекул
- •2.2 Работа газа при изменении его объема
- •Бегущая монохроматическая волна
- •Стоячая монохроматическая волна
Закон Гука в простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:
F=
- kдельтаx,где ![]() —
жёсткость тела,
—
жёсткость тела, ![]() —
величина деформации
.Относительное
удлинение e=дельта
x/x0Сила
упругости, возникающая при деформации
тела, прямо пропорциональна удлинению
тела и направлена противоположно
направлению перемещения частиц тела
относительно других частиц при
деформации.
Деформация изгиба –mg.Деформация
растяжения- сжатия.
—
величина деформации
.Относительное
удлинение e=дельта
x/x0Сила
упругости, возникающая при деформации
тела, прямо пропорциональна удлинению
тела и направлена противоположно
направлению перемещения частиц тела
относительно других частиц при
деформации.
Деформация изгиба –mg.Деформация
растяжения- сжатия.
силы трения Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Она всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей. Законы трения связаны с электромагнитным взаимодействием, которое существует между телами. 1Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя).2Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ). 1Сухое трение возникает между поверхностями твердых тел в отсутствие смазки.2 Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями. Сухое трение, в свою очередь, подразделяется на трение 1скольжения и трение 2качения.
законы сухого трения
|
|
Подействуем на
тело, лежащее на неподвижной плоскости,
внешней силой ,
постепенно увеличивая ее модуль. Вначале
брусок будет оставаться неподвижным,
значит, внешняя сила фвнешняя уравновешивается
некоторой силой фтр,
направленной по касательной к трущейся
поверхности, противоположной силе фтр.
В этом случае фтр и
есть сила трения покоя.Установлено,
что максимальная сила трения покоя не
зависит от площади соприкосновения
тел и приблизительно пропорциональна
модулю силы
нормального давления N:![]()
μ0 – коэффициент трения покоя, зависящий от природы и состояния трущихся поверхностей.
|
|
|
где μ – коэффициент трения скольжения. Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится. Сила трения качения подчиняется тем же законам, что и сила трения скольжения, но коэффициент трения μ ; здесь значительно меньше.
На тело,
находящееся на наклонной плоскости с
сухим трением, действуют три силы: сила
тяжести ![]() ,
нормальная сила реакции опоры
,
нормальная сила реакции опоры ![]() и сила сухого трения
и сила сухого трения ![]() .
Сила
.
Сила ![]() есть
равнодействующая сил
и
;
она направлена вниз, вдоль наклонной
плоскости.
есть
равнодействующая сил
и
;
она направлена вниз, вдоль наклонной
плоскости.
F = mg sin α, N = mg cos α. |
|
Если ![]() –
тело остается неподвижным на наклонной
плоскости. Максимальный угол наклона
α определяется из условия
(Fтр)max = F
или μ mg cosα = mg sinα,
следовательно, tg αmax = μ,
где μ – коэффициент сухого
трения.Fтр =
μN = mg cosα, F
= mg sinα.
–
тело остается неподвижным на наклонной
плоскости. Максимальный угол наклона
α определяется из условия
(Fтр)max = F
или μ mg cosα = mg sinα,
следовательно, tg αmax = μ,
где μ – коэффициент сухого
трения.Fтр =
μN = mg cosα, F
= mg sinα.
При α > αmax тело будет скатываться с ускорениемa = g ( sinα - μ cosα ), Fск = ma = F - Fтр. Если дополнительная сила Fвн, направленная вдоль наклонной плоскости, приложена к телу, то критический угол αmax и ускорение тела будут зависеть от величины и направления этой внешней силы.
центр масс
![]()
![]() — радиус-вектор центра
масс,
— радиус-вектор центра
масс,![]() —
радиус-вектор i-й
точки системы,
—
радиус-вектор i-й
точки системы,![]() —масса i-й
точки.
—масса i-й
точки.
Для случая непрерывного распределения масс:
![]()
![]()
![]() —
суммарная масса
системы,
—
суммарная масса
системы,![]() —
объём,
—
объём,![]() —
плотность.
—
плотность.
Понятие центра масс широко используется в физике.
Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.
Теорема
о движении центра масс.![]()
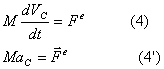
(4’) – выражает теорему о движении центра масс системы: центр масс системы движется как материальная точка, на которую действуют все силы системы.
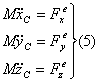
Выводы:Внутренние
силы не оказывают влияния на движение
центра масс системы.Если ![]() ,
движение центра масс системы происходит
с постоянной скоростью.
,
движение центра масс системы происходит
с постоянной скоростью.![]() ,
то движение центра масс системы в
проекции на ось
,
то движение центра масс системы в
проекции на ось ![]() происходит
с постоянной скоростью.Теорема об
изменении момента количества движения
системы (кинетического момента).
происходит
с постоянной скоростью.Теорема об
изменении момента количества движения
системы (кинетического момента).
система мат точек
Механическая система (система материальных точек) - это совокупность конечного числа материальных точек, выделенных для рассмотрения.
Внутренние силы - это силы, с которыми точки системы действуют друг на друга.
Внешние силы - это силы, источники которых лежат вне системы, т.е. это силы, действующие со стороны тел, не принадлежащих системе.
Это условное разделение сил, зависит от выбора системы точек. Замкнутая (изолированная) система материальных точек или материальная точка - это система, в которой отсутствуют внешние силы (или воздействие посторонних тел пренебрежимо мало).
В неинерциальных системах отсчета к внешним силам относят силы инерции. В таких системах всегда присутствуют внешние силы, то есть замкнутые системы возможны в случае инерциальных систем отсчета
ИСО – 1 зн ньютона. геоцентрическая, гелиоцентрическая
Принцип относительности Галилея
Из
формулы для ускорений следует, что если
движущаяся система отсчета движется
относительно первой без ускорения, то
есть ![]() ,
то ускорение
,
то ускорение ![]() тела
относительно обеих систем отсчета
одинаково.
тела
относительно обеих систем отсчета
одинаково.
Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим закон инерции, и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.
Классическая механика постулирует следующие два принципа:
время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;
пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.
Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона.
Основное уравнение динамики относительного движения материальной точки имеет вид:
![]() ,
,
где ![]() — масса тела,
— масса тела, ![]() —
ускорение тела относительно неинерциальной
системы отсчёта,
—
ускорение тела относительно неинерциальной
системы отсчёта, ![]() —
сумма всех внешних сил, действующих на
тело,
—
сумма всех внешних сил, действующих на
тело, ![]() — переносное
ускорение тела,
— переносное
ускорение тела, ![]() — кориолисово
ускорение тела.
— кориолисово
ускорение тела.
Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:
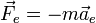 —
переносная сила
инерции
—
переносная сила
инерции
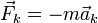 — сила
Кориолиса
— сила
Кориолиса
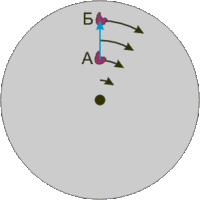
Траектории шарика при движении по поверхности вращающейся тарелки в разных системах отсчета (вверху — в инерциальной, внизу — в неинерциальной).
Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.
Для
того, чтобы тело двигалось с кориолисовым
ускорением, необходимо приложение силы
к телу, равной ![]() ,
где
,
где ![]() —
кориолисово ускорение. Соответственно,
тело действует по третьему закону Ньютона с
силой противоположной направленности.
—
кориолисово ускорение. Соответственно,
тело действует по третьему закону Ньютона с
силой противоположной направленности. ![]() Сила,
которая действует со стороны тела, и
будет называться силой Кориолиса. Не
следует путать Кориолисову силу с
другой силой
инерции — центробежной
силой,
которая направлена
по радиусу вращающейся окружности.
Сила,
которая действует со стороны тела, и
будет называться силой Кориолиса. Не
следует путать Кориолисову силу с
другой силой
инерции — центробежной
силой,
которая направлена
по радиусу вращающейся окружности.
Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
![]() ,где
—
точечная масса,
,где
—
точечная масса, ![]() — вектор угловой
скорости вращающейся
системы отсчёта,
— вектор угловой
скорости вращающейся
системы отсчёта, ![]() —
вектор скорости движения точечной
массы в этой системе отсчёта, квадратными
скобками обозначена операция векторного
произведения.
—
вектор скорости движения точечной
массы в этой системе отсчёта, квадратными
скобками обозначена операция векторного
произведения.
Величина ![]() называется
кориолисовым ускорением.
называется
кориолисовым ускорением.

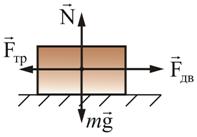
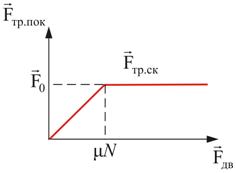
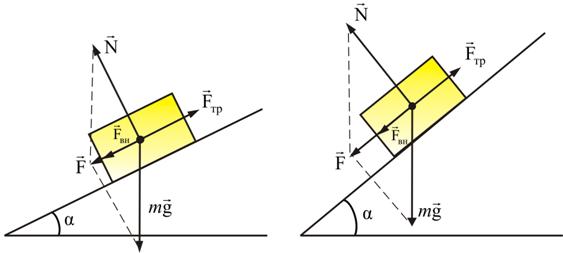 Рис.
4.7
Рис.
4.7