Третий закон Ньютона: силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению:

,где – сила, действующая на первое тело со стороны второго, – сила, действующая на второе тело со стороны первого. Из третьего закона следует, что в любой механической системе материальных точек геометрическая сумма всех внутренних сил (т.е. сил, с которыми взаимодействуют между собой материальные точки системы) равна нулю.

2.2 Динамика вращательного движения твердого тела Вращательное действие силы характеризуется моментом силы относительно точки (рис. 5а) и относительно оси (рис. 5б). Для того чтобы определить момент силы относительно точки О, проведем из точки О радиус-вектор в точку приложения силы (рис. 5а). Моментом силы относительно точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора на силу : Модуль момента силы M = rFsin = Fd, где d = rsin – плечо силы.Для того чтобы определить момент силы относительно оси Z, выберем на оси Z произвольную точку, найдем момент силы относительно этой точки, а затем спроецируем на ось Z момент силы относительно точки. Таким образом, момент силы относительно оси – величина скалярная.Разложим силу на три составляющие (рис. 5б): – осевая, параллельная оси вращения, – радиальная, перпендикулярная оси вращения, – касательная, перпендикулярная и оси вращения. Составляющую можно определить как проекцию силы на направление вектора , направленного по касательной к окружности радиусом R, проведенной через точку приложения силы перпендикулярно оси вращения. Направление вектора образует с осью Z правовинтовую систему. Составляющие и вращения тела относительно оси Z не вызывают. Вращающее действие силы обусловлено составляющей . Можно показать, что момент силы относительно оси Z

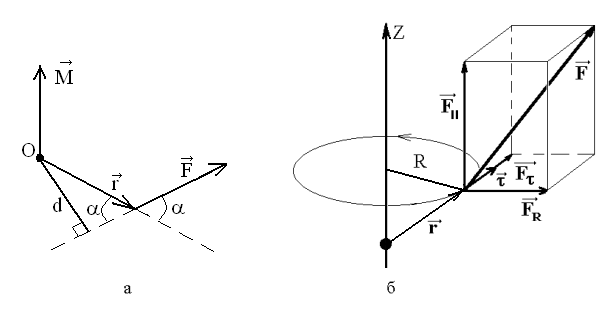
Рис. 5

Инертные свойства тела при вращательном движении характеризует момент инерциииииииииииииинерции. Он зависит от распределения массы тела относительно оси вращения. Момент инерции материальной точки массой m, находящейся на расстоянии r от оси: . – момент инерции системы материальных точек; – момент инерции тела, где – плотность тела.

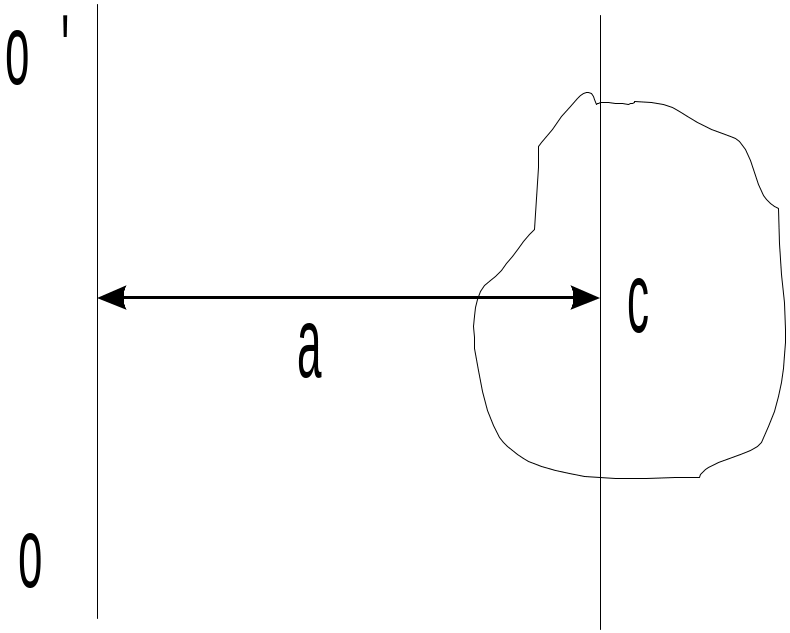
Рис. 6

Момент инерции тела относительно произвольной оси может быть рассчитан по теореме Штейнера: моментинерции тела относительно оси O'O равен сумме момента инерции тела относительно оси, проходящей через центр инерции и параллельной O'O, и произведения массы тела на квадрат расстояния между осями (рис. 6): .Моментом импульса материальной точки относительно некоторой точки называется векторная величина, равная векторному произведению радиуса-вектора на импульс материальной точки (рис. 7а): .

Моментом импульса системы материальных точек называется геометрическая сумма моментов импульсов точек, составляющих систему: .Моментом импульса материальной точки относительно оси Z называется скалярная величина, равная проекции момента импульса относительно произвольной точки, лежащей на оси Z, на эту ось. Аналогично моменту силы относительно оси, момент импульса относительно оси Z

где p_ – проекция импульса на направление вектора , направленного по касательной к окружности радиусом, проведенной через материальную точку перпендикулярно оси вращения (рис. 7б). Направление вектора образует с осью Z правовинтовую систему.

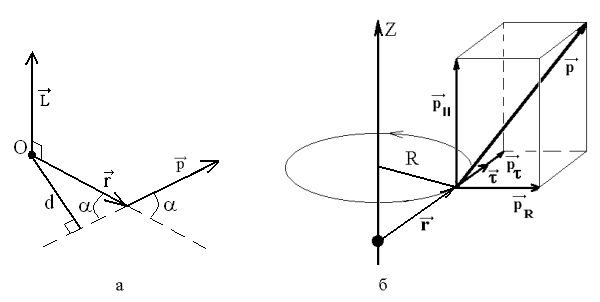
Рис. 7Момент импульса тела относительно оси вращения L_Z = I_Z_Z,где I_Z – момент инерции тела относительно оси Z, _Z – проекция угловой скорости тела на ось Z. Для однородного тела, вращающегося относительно оси симметрии: .

Основной закон динамики вращательного движения:

Скорость изменения момента импульса тела относительно оси равна результирующему моменту внешних сил относительно этой же оси (проекция углового ускорения на ось пропорциональна результирующему моменту внешних сил относительно оси и обратно пропорциональна моменту инерции тела относительно этой же оси): Из законов динамики поступательного и вращательного движений следует условие равновесия тел: 3. Работа и механическая энергия3.1 Работа и мощность при поступательном и вращательном движениях

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой. Элементарной работой силы называется величина, равная скалярному произведению силы на элементарное перемещение : ,где – элементарный путь точки приложения силы за время dt,  – угол между векторами и .

Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом: .Если = const, то А=  .При вращательном движении работа определяется проекцией момента сил на направление угловой скорости: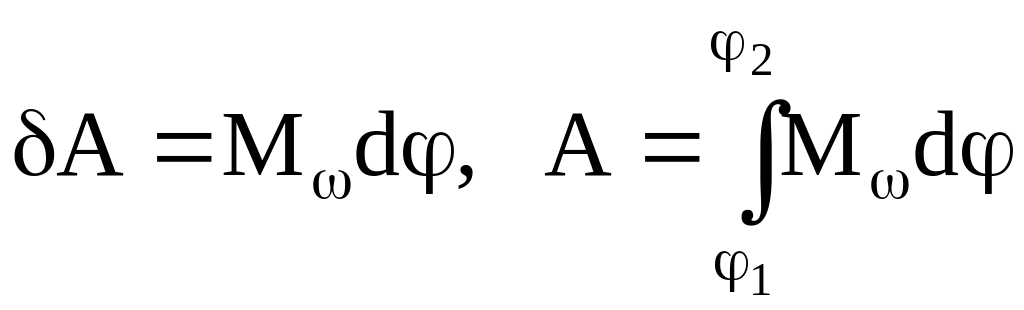 ,если М_ = const, то А = М_.Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени: средняямощность; – мгновенная мощность.При вращательном движении мощность определяется следующим образом: .

3.2 Консервативные и неконсервативные силы

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.