1. Основные геометрические образы в курсе начертательной геометрии, аксиоматика курса. Инвариантные свойства параллельного проецирования.
Основные понятия:
Графика - способ отображения окружающей действительности на плоскости.
Рисунок – изображение на “глаз”.
Чертеж – Графическое изображение, выполненное при помощи чертежных инструментов и принадлежностей по особым правилам построения изображений , которое дает полное представление о внешних и внутренних устройствах.
Изделие - предмет или набор предметов для изготовления.
Сборочная единица – изделие, составные части которой подлежат соединению между собой.
Комплект – набор предметов для определенного назначения.
Комплекс – совокупность чего либо, образующее одно целое.
На чертежах изображаются: детали, сборочные единицы, комплекты и комплексы.
Инвариантные свойства параллельного проецирования.
Определение: Свойства геометрических фигур остающиеся неизменными в процессе проецирования называются независимыми или инвариантными для данного аппарата проецирования.
Свойства:
1. Проекция точки есть точка.
2. Проекция прямой есть прямая.
3. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых.
4. Проекции параллельных прямых параллельны.
5. Прямая, параллельная направлению проецирования, проецируется в точку.
2. Метод проекции (операции), аппарат проецирования.
1. Центральное проецирование
Центральное проецирование представляет собой общий случай проецирования геометрических образов из центра на плоскость.
2. Параллельное проецирование
Параллельное проецирование можно рассматривать как частный случай центрального проецирования с бесконечно удаленным центром проекций. Осуществляется оно пучком параллельных проецирующих лучей заданного направления.
3. Ортогональное проецирование
Если направление проецирующих лучей перпендикулярно плоскости проекций, то такой вид называется ортогональным.
Аппарат проецирования включает в себя проецирующие лучи, проецируемый объект и плоскость, на которой получается изображение оригинала.
Проецированием называется процесс построения изображения предмета на плоскости – бумаге и т.д.
3. Комплексный чертеж. Определение координат на комплексном чертеже.
Комплексный чертеж - это совокупность двух или более взаимосвязанных ортогональных проекций геометрической фигуры, расположенной на одной плоскости чертежа.
Метод координат
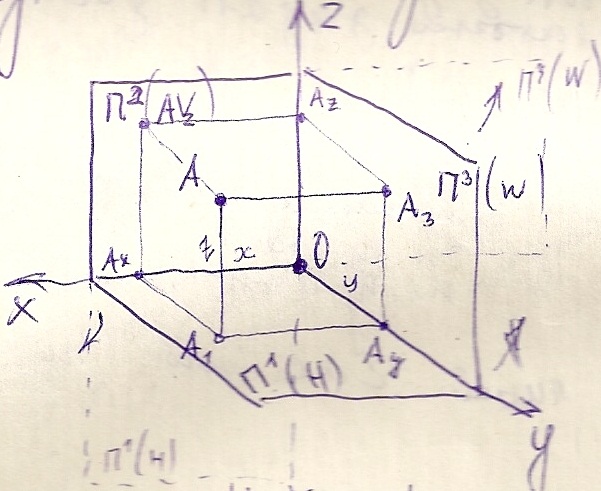
Декарт предложил П1,П2,П3 назвать координатными плоскостями соответственно H,V,W ,а оси Ox,Oy,Oz – осями координат, где
Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат.
Тогда A(x,y,z) – координаты точки A.
4. Способы задания прямой на комплексном чертеже, частные положения прямой.
Прямая на комплексном чертеже может быть задана проекциями прямой; проекциями двух точек, принадлежащих прямой; проекциями отрезка прямой.
Частные положения прямой
Прямая общего положения - прямая, произвольно расположенная относительно плоскости проекции.
Горизонтальная прямая - это прямая, параллельная горизонтальной плоскости проекций π1.
Профильная прямая - это прямая, параллельная профильной плоскости проекций π3.
Фронтальная прямая - это прямая параллельная фронтальной плоскости проекций π 2.