Экзаменационный билет №___20____

1. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ: ПОСТАНОВКА ЗАДАЧИ, ШАГОВЫЙ МЕТОД.

Пусть имеется уравнение F(x)=0, причем можно считать, что все интересующие вычислителя корни находятся на отрезке [А; В], в котором функция F(x) определена, непрерывна и F(A)*F(B)< 0. Требуется отделить корни уравнения, т. е. указать все отрезки [а; b] [А; B], содержащие по одному корню. Будем вычислять значения F(x), начиная с точки х=А, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция f(x) монотонна на этом отрезке, так соответствующие значения аргумента х (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

2. Перевести A₂=101110,101_2, A₈=125,46_8, A₁₆=2AF,C4₁₆ в десятичное. Выполнить перевод числа 0,847 в двоичную систему счисления

Экзаменационный билет №___21____

1. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ: ПОСТАНОВКА ЗАДАЧИ, МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ.

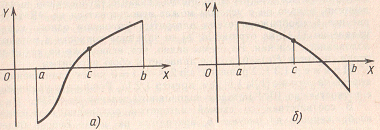
Пусть уравнение функции рисунка имеет на отрезке [а;b] единственный корень причем функция F(x) на этом отрезке непрерывна. Разделим отрезок [а; b] пополам точкой с = (а + b)/2. Если F(c) ≠0 (что практически наиболее вероятно), то возможны два случая: либо F(x) меняет знак на отрезке [a;c] (рис 3, а), либо на отрезке [с; b] (рис. 3, б). F(a)*F(с)<0 (функция в точке а и в точке с имеет разный знак). Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и, продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

2. Перевести 756, 35 в двоичную систему. Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод выполнить до трех значащих цифр.

Экзаменационный билет №___22____

1. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ: ПОСТАНОВКА ЗАДАЧИ, МЕТОД НЬЮТОНА

Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить уравнение это значит найти такое x, при котором уравнение превращается в тождество. В общем случае уравнение может иметь 0; 1; 2;...∞ корней. Рассмотренные ниже численные методы решения нелинейных уравнений позволяют находить один корень на заданном интервале [a,b]. При этом на интервале должен существовать только один корень. Рассмотрим несколько методов решения нелинейных уравнений.

Ньютона метод, метод приближённого нахождения корня x₀ уравнения f(x) = 0, называемый также методом касательных. Н. м. состоит в том, что по исходному ("первому") приближению x = a₁ находят второе (более точное), проводя касательную к графику (см. рис.) у = f(x) в точке А до её пересечения с осью Ox; точка пересечения и принимается за новое значение a₂. корня. Повторяя в случае необходимости этот процесс, получают всё более и более точные приближения a₂, a₃... корня x₀ при условии, что производная f’(x) монотонна и сохраняет знак на сегменте, содержащем x₀.

2. Перевести 124₁₀ в восьмеричную, 174₈ в десятичную Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D₁₆