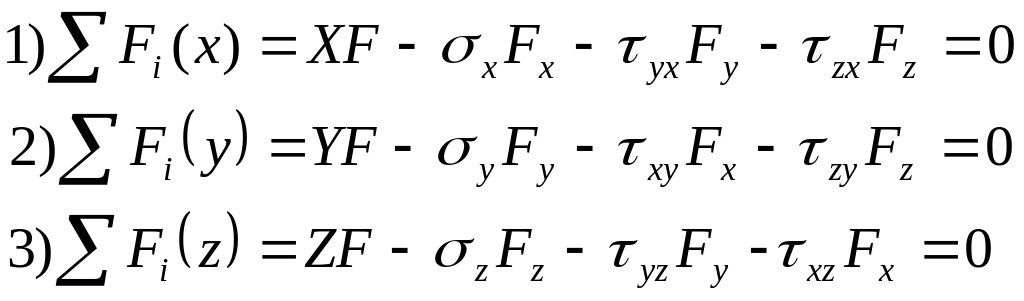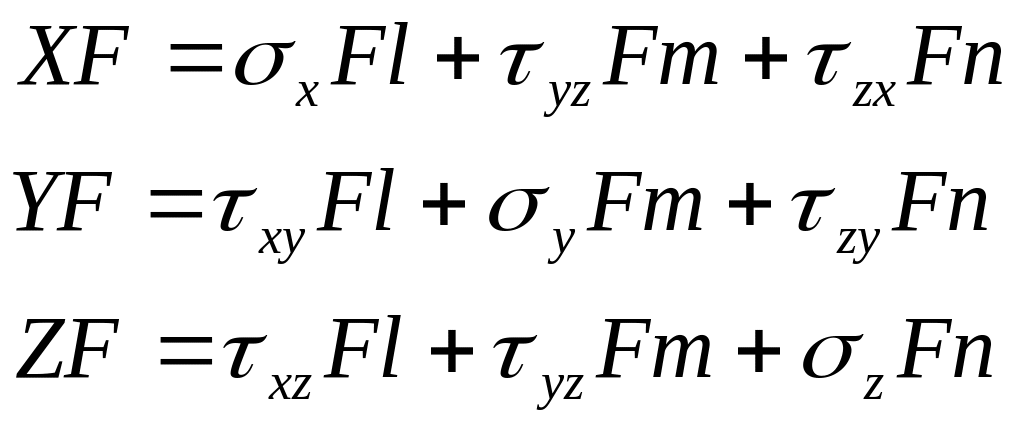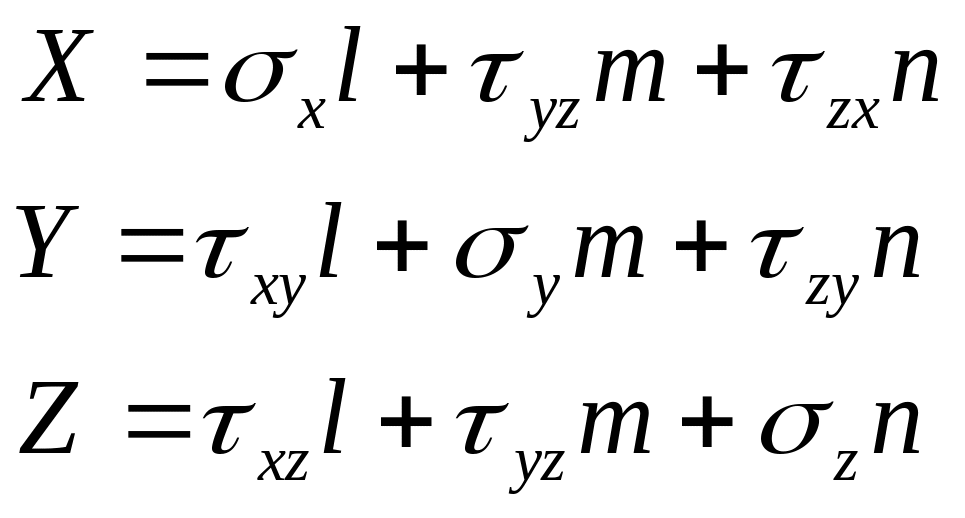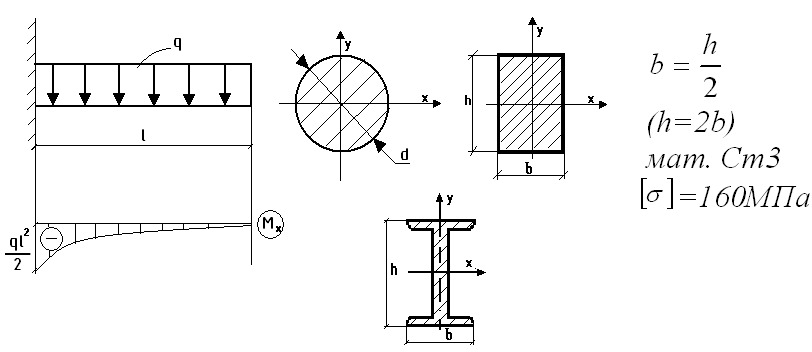
44 Рациональные типы сечения балок.
Спроектировать балку рационального сечения означает задать ей такие размеры и формы, которые обеспечивали выполнение условия прочности при минимальном расходе материала. Несущая способность балок пропорциональна моменту сопротивления сечения, т.е. Mx↔Wx
Mx=[σ]Wx
Расход материала пропорционален площади поперечного сечения.
Рассмотрим на примере, какое из представленных сечений является более рациональным.
Условие прочности при изгибе:
а) для круглого поперечного сечения:
б) для прямоугольного поперечного сечения:
в) для двутаврового сечения:
Б
лижайшее
значение WxГОСТ=317
см3 ,
что соответствует двутавру №24 «а»:
h=24cm=0,24m
b=0,1m
Fдвутв=37,5cm2
Двутавровое сечение оказалось наиболее рациональным, т.к. чем меньше площадь поперечного сечения балки, тем оно экономичнее, а балка легче и дешевле.
Круглое – наименее рациональное сечение.
Коэффициент экономичности сечения:
d=h=hдвут
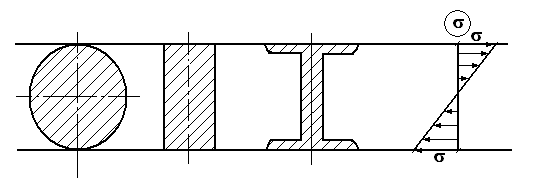
Основная часть нагрузки воспринимается верхней и нижней образующими сечение, т.к. на них напряжения максимальны, чем ближе к центру тяжести сечения, тем напряжения минимальны.
45 Чем определяется экономичность сеч-я балки
чем меньше площадь поперечного сечения балки, тем оно
экономичнее, а балка легче и дешевле.
46 Балки равного сопротивления.
Балкой равного сопротивления называется балка, в которой момент сопротивления сечения изменяется пропорционально изгибающему моменту.
В балках равного сопротивления изгибу в любом сечении нормальные напряжения одинаковы и равны допускаемым напряжениям.
в
любом сечении, на любом dz.
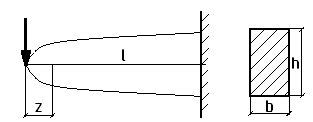
Примером балки равного сопротивления может служить консоль прямоугольного сечения.
a)
b=const, h=f(z);
b) h=const, b=f(z)
П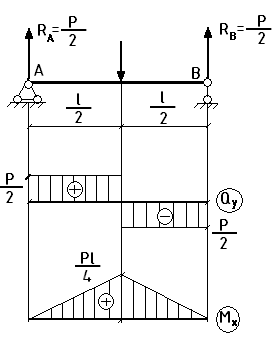
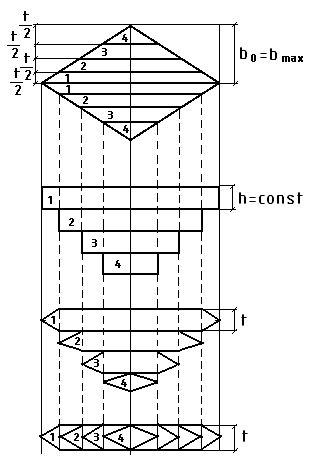араболическая
балка (а) неудобна в изготовлении, поэтому
на практике практически не применяется.
-
линейная зависимость
Примером балки равного сопротивления изгибу может служить рессора.
В рессоре момент сопротивления сечения Wx и [σ] – напряжение – постоянны в любом сечении на любой длине z от опоры.
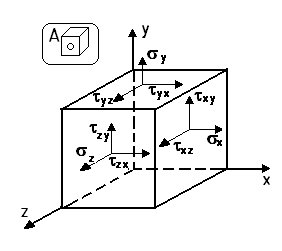
47. Напряженное состояние в точке; основные понятия; закон парности касательных напряжений; тензор напряжений
Совокупность напряжений, действующих на различные площадки, проведенных через точки тела, характеризует напряженное состояние в окрестности данной точки.
Закон парности касательных напряжений.
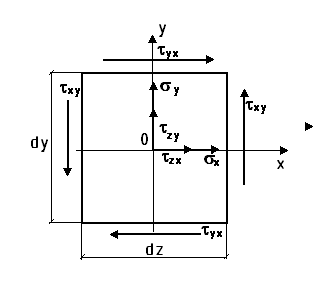
Касательные напряжения по двум взаимно перпендикулярным площадкам всегда равны по величине и направлены навстречу друг другу или наоборот.
Напряженное состояние в точке определяется 6 компонентами: σx, σy, σz, τxy=τyx, τyz=τzy, τzx=τxz.
Т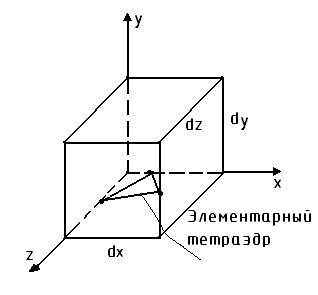
ензор
напряжения –
матрица вида:
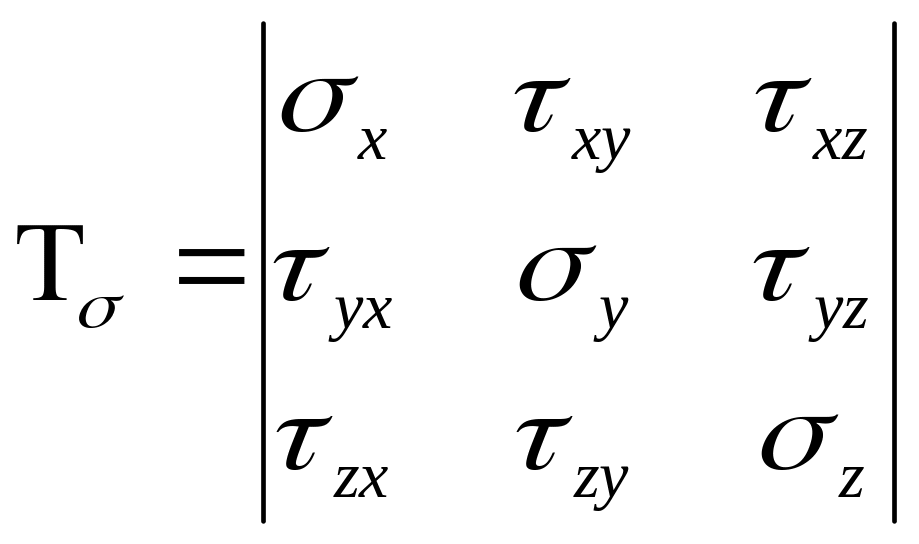
ν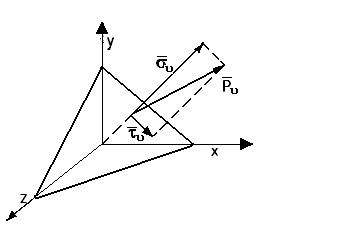
- внешняя нормаль к наклонной площадке;
-
вектор полного напряжения;
-
вектор нормального напряжения;
-
вектор касательного напряжения.
48. Дайте определение главным направлениям, главным площадкам и главным напряжениям
Главное направление – это направление нормалей к главным площадкам.
Главное напряжение – это напряжение возникающие на главных площадках.
Главные площадки – это 3 взаимно перпендикулярные площадки в любой точке нагруженного тела, на которых отсутствуют касательные напряжения.
49. Определение напряжений на произвольно ориентированной площадке. Условия на поверхности
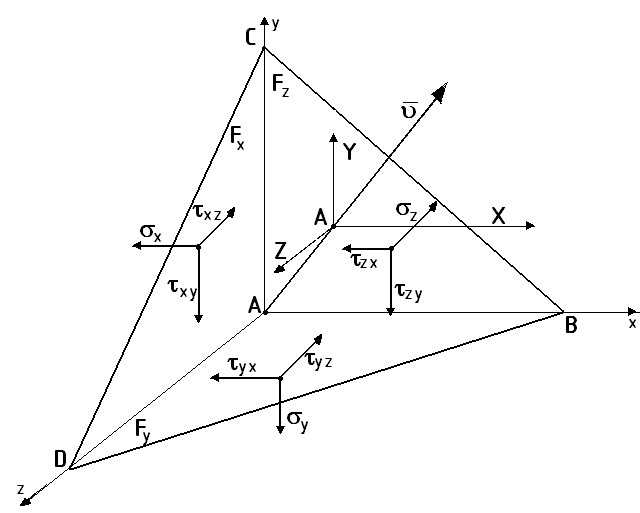или
X,
Y,
Z
– проекции вектора
на оси x,
y,
z.
Обозначим
Площадь
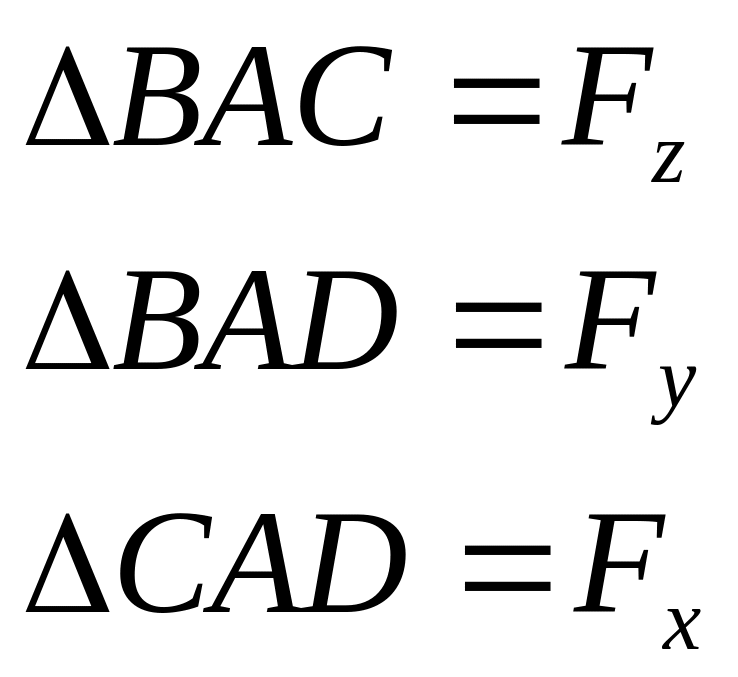
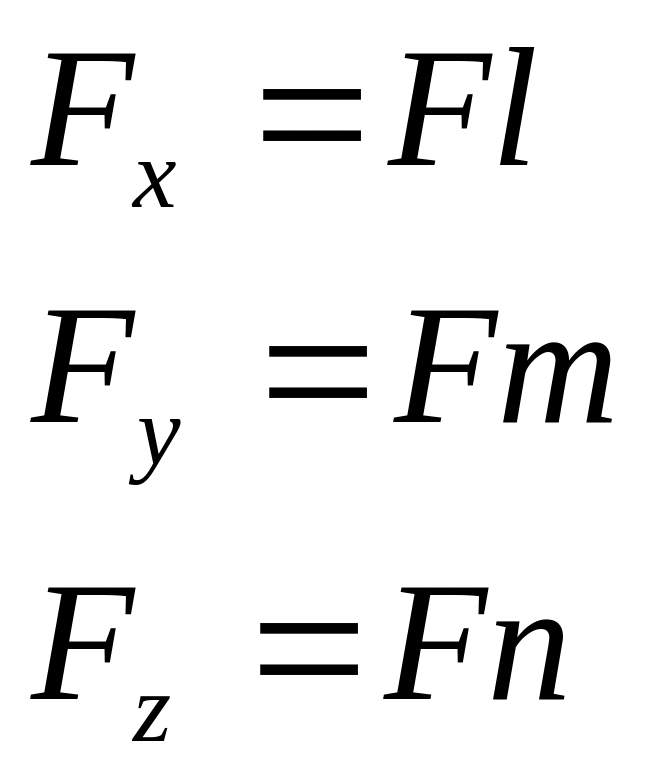
Спроектируем все силы на соответственные оси координат:
