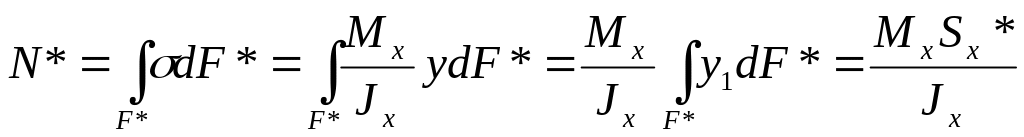1 ). Для поперечных сил:
2).Для изгибающих моментов:
Эпюры для моментов всегда строятся на сжатом волокне.
40 Дифференциальные зависимости при изгибе.
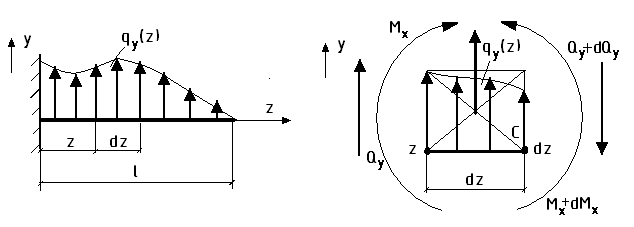
1).∑Fi(Y)=Qy+qy(z)dz-(Qy+dQy)=0
qy(z)dz - dQy=0
2).
Qydz=dMx
→
Теорема Журавского: полная производная, взятая по длине от поперечной силы, равна интенсивности распределения нагрузки.
Полная производная от изгибающего момента, взятая по длине, равна поперечной силе.
Вторая производная от изгибающего момента равна интенсивности распределенной нагрузки.
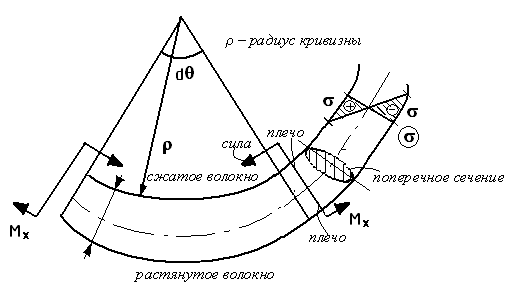
41 Нормальные напряжения при изгибе.
EJx – изгибная жесткость
=к
– кривизна
-
формула Навье
Знак ± в формуле Навье принадлежит координате у.
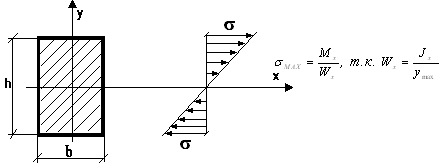
Для стандартных ГОСТовских профилей, определяемых сортаментом, геометрические характеристики Jx, Wx заданы.
Номер двутавра соответствует его высоте в см.
42 Касательные напряжения при поперечном изгибе. Формула Журавского.
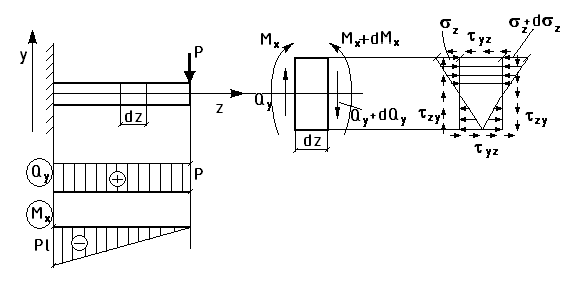
Касательные напряжения ввиду своей парности всегда именуются двумя индексами: 1-й индекс соответствует той оси, которой они перпендикулярны,
2-индекс соответствует оси, которой они параллельны.
|
|
|
|
|
(1) |
|
|
|
(2) |
(1)=(2):
-
формула Журавского
Qy – поперечная сила – const для любой точки поперечного сечения;
Jx – момент инерции сечения – постоянная величина для всего сечения относительно оси Х;
b – ширина сечения в рассматриваемой точке, b≠const;
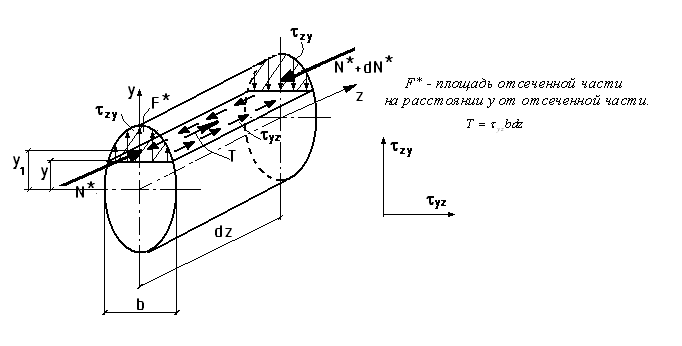
Sx* - статический момент отсеченной части сечения площадью F*:
Максимального значения касательные напряжения достигают в центре тяжести сечения: статический момент максимален из-за максимального значения площади F*.
Минимального значения касательные напряжения достигают по верхней и нижней границе сечения.
Пример:
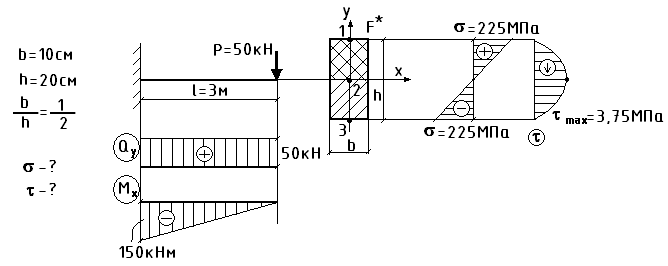
Опасное сечение – заделка.
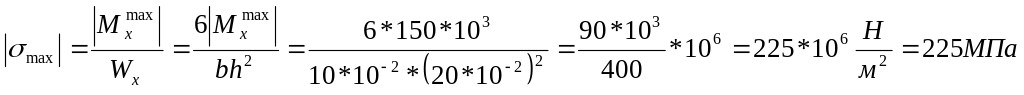
(для
прямоугольника)
При проведении прочностных расчетов из-за малости касательных напряжений ими часто пренебрегают.
Формула Журавского справедлива для достаточно узких и высоких профилей балки: b<<h, т.к. предполагается, что касательные напряжения равномерно распределены по ширине сечения, что подтверждается экспериментально.
Для балок иных профилей формула Журавского носит приближенный характер
43 Расчеты на прочность при изгибе.
Условие
прочности:
При проведении проверочных расчетов сравниваются нормальные максимальные напряжения с напряжениями допускаемыми.
Из условия прочности выражают:
А)при подборе сечения – момент сопротивления сечения;
Б)при определении допускаемого изгибающего момента:
