7.6. Электроприводы с модальным управлением. Наблюдающие устройства

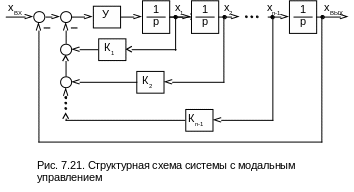
Идею модального управления поясним, пользуясь структурной схемой (рис. 7. 21). Допустим, что требуется выполнить замкнутую систему регулирования выходной координаты, так что Х_ВХ = Х_ВЫХ. При этом неизменяемая часть системы представлена последовательным соединением n интегральных звеньев с промежуточными переменными Х₁, Х₂, ..., Х_N-1. Для простоты у всех этих звеньев постоянные времени приняты равными 1 с, но это непринципиально. Ясно, что непосредственно замкнуть контур регулирования по выходной координате Х_ВЫХ не удастся, так как получится структурно неустойчивая система.

Мы поступим несколько иначе, разбив решение задачи на ряд этапов. Сначала выполним контур регулирования Х₁, для чего охватим регулятор У и первое интегрирующее звено неизменяемой части системы местной отрицательной обратной связью по Х₁ с коэффициентом усиления К₁. Получившийся контур регулирования 1 не имеет ограничений по условием устойчивости, так как безынерционной обратной связью охватывается звено первого порядка. По этой причине частоту среза контура 1 можно сделать сколь угодно высокой. После завершения настройки контура 1 выполним отрицательную обратную связь по переменной Х₂, а настройку контура регулирования 2 выполним, изменяя коэффициент усиления К₂ канала отрицательной обратной связи по Х₂. Повторяя последовательно процедуру охвата обратными связями все большего числа звеньев, установленных в прямом канале регулирования, реализуем в конечном итоге и внешний контур регулирования по переменной Х_ВЫХ. При этом величины коэффициентов обратных связей могут быть выбраны с использованием любых общепринятых методов синтеза. В частности, при частотном подходе величину частоты среза каждого последующего контура регулирования следует выбирать в 2...4 раза ниже, чем предыдущего, так как в каждом новом контуре добавляется по одному интегрирующему звену.

Так как во внутреннем контуре 1 нет ограничения по быстродействию, то соответствующим выбором коэффициентов усиления К₁, К₂, ... , К_N можно получить любые заранее заданные показатели качества регулирования. Если объект регулирования, кроме интеграторов в прямом канале регулирования, содержит также набор местных обратных связей, то простым преобразованием структурной схемы эти связи могут быть приведены ко входу общего усилителя У и затем просуммированы с вводимыми обратными связями.

Переменные Х₁, Х₂, ..., Х_N = Х_ВЫХ принято называть переменными состояния системы. Совокупность же обратных связей по всем переменным состояния с коэффициентами усиления К₁, К₂, ... , К_N образует так называемый модальный регулятор.

В общем случае переменными состояния системы принято называть набор наименьшего числа независимых переменных, однозначно определяющих динамическое состояние системы в любой момент времени на отрезке [t₀, t₁], если заданы их начальные значения в момент времени t = t₀ и известны в любой момент времени на отрезке [t₀, t₁] внешние воздействия. В частном случае, когда уравнения системы представлены в нормальной форме (Коши) за переменные состояния удобно принять выходную координату и набор всех ее производных.

Применительно к следящему электроприводу, динамика которого описывается структурной схемой (рис. 7.13), за переменные состояния следует принять, кроме выходной координаты _ВЫХ, также скорость выходного вала РМ n₂, момент упругого звена М₂, скорость входного вала (вала двигателя) n₁, ток якоря двигателя I_Я. Если бы удалось выполнить многоконтурную систему регулирования с полным набором всех указанных обратных связей, то динамические показатели такой системы были бы весьма высоки. Однако на пути реализации этой системы стоят существенные как технические трудности (сложно выполнить некоторые из датчиков, например, момента М₂ или скорости n₂), так и конструктивные и экономические (сама система с полным набором указанных датчиков будет весьма дорогой и громоздкой). По этой причине в современных системах электропривода очень часто отказываются от прямого измерения переменных состояния и переходят к вычислению этих переменных с помощью специальных узлов, именуемых наблюдателями.

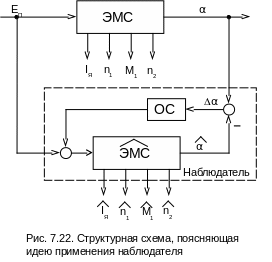Идею наблюдателя поясняет схема (рис. 7.22). Предположим, что движение электромеханической системы ЭМС производится изменением ЭДС преобразователя Е_П, а выходной координатой её является угловое положение вала  исполнительного органа. Промежуточные переменные I_Я, n₁, M, n₂ являются ненаблюдаемыми и необходимо их как-то вычислить. Поступим следующим образом. Выполним модель ЭМС. Ее можно реализовать, например, используя стандартные операционные усилители и набирая с их помощью регуляторы, имеющие тот же тип передаточных функций, что звенья Д, УЗ, РМ, И, входящие в ЭМС. При этом напряжения на выходах соответствующих регуляторов оказываются аналогичны истинным I_Я, n₁, M, n₂ и . Благодаря существованию аналогии между промежуточными переменными реальной ЭМС и напряжениями на выходах соответствующих звеньев на модели этой ЭМС последние принято обозначать теми же буквами, что и сами переменные, но со знаком «» над переменной, что облегчает понимание процессов. Сами же напряжения на выходах регуляторов принято называть оценками соответствующих переменных. Например, n₂ есть оценка истинной скорости n₂.

Сказать, что оценки переменных в точности равны соответствующим переменным нельзя, так как модель не учитывает действие в реальной схеме возмущений и нестабильности параметров. Чтобы названное расхождение уменьшить, измеряемую выходную координату ЭМС (в нашем случае это – угловое положение выходного вала ) сравнивают с ее оценкой и в функции этой разности  корректируют показания модели. С этой целью модель ЭМС^* охватывают местной отрицательной обратной связью ОС. Совокупность модели ЭМС^* и местной обратной связи ОС, предназначенных для вычисления переменных состояния реальной системы, образует наблюдающее устройство (наблюдатель).

В простейшем случае звено ОС – это безынерционное звено с коэффициентом усиления К_ОС. Естественно, чтобы добиться большей точности работы модели, коэффициент усиления К_ОС стремятся иметь максимально высоким. Но в этом случае встает проблема устойчивости наблюдателя. Чтобы иметь достаточно высокую точность наблюдения (воспроизведения) переменных и не нарушать условий устойчивости наблюдателя, звено ОС выбирают с передаточной функцией вида

W_ОС (p) = K_ОС + T₁ p + Т₂² р + ...,

где порядок старшей производной выбирают на единицу меньше порядка уравнения модели ЭМС^*. Чтобы слагаемые в выражении для передаточной функции ОС, пропорциональные первой и последующим идеальным производным по ошибке наблюдения , были технически реализуемы, их подают на входы регуляторов, стоящих за первым, вторым и последующими интегрирующими з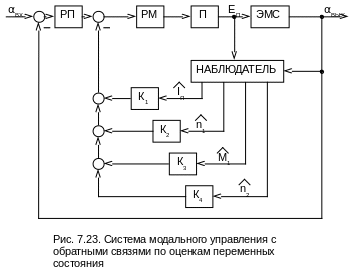 веньями. Когда наблюдатель настроен, то с выходов его звеньев можно брать сигналы по оценкам переменных состояния ЭМС и использовать эти сигналы как местные корректирующие связи при настройке контура регулирования положения (см. рис. 7.23). Здесь на вход модального регулятора РМ через звенья с коэффициентами усиления К₁, К₂, К₃, К₄ подаются сигналы местных обратных связей по оценкам переменных состояния. Внешний контур регулирования настраивается регулятором положения РП. Внутренняя структура звена ЭМС соответствует схеме (рис. 7.13). Правда, в этом случае, строго говоря, оценки переменных будут отличаться от своих переменных, так как наблюдатель корректируется не пропорциональным звеном, а содержит производные по ошибке . Однако в [8] показано, что система модального управления, выполненная по такому принципу, имеет динамические показатели, что и система, выполненная по самим переменным состояния.

На рис. 7.24 приведен пример функциональной схемы наблюдателя, восстанавливающего недостающие переменные состояния в ЭМС, структурная схема которого рассмотрена нами

ранее (рис. 7.13). Здесь апериодическим регулятором 1 моделируется двигатель постоянного тока, а интегральными регуляторами 2, 3 и 4 – звенья УЗ, РМ и И. Пропорциональные регуляторы 6 и 7 соответствуют местным обратным связям по упругому моменту и скорости вала РМ. Сигнал ошибки наблюдения  подается на входы регуляторов 1, 2, 3 и 4 с выходов регуляторов 5 и 8. Регулятор 8 является инвертором.

Модальное управление – очень эффективный способ достижения высоких динамических показателей в сложных динамических системах. На это преимущество обращают внимание разные авторы [8, 16, 27]. Но не следует преувеличивать его возможности, когда заходит речь об условиях настройки реальных систем электропривода. Прежде всего, гипотеза о возможности получения в системе регулирования с модальным регулятором любых наперед заданных динамических показателей молчаливо предполагает отсутствие ограничений по быстродействию в самом внутреннем контуре регулирования, где оптимизация производится изменением величины коэффициента К₁. Но как раз в этом-то контуре и наблюдается ограничение предельного значения его частоты среза, что обусловлено необходимостью учета влияния помех в ходе повышения быстродействия настраиваемого контура, а также необходимостью учета дискретного характера работы вентильных преобразователей в зоне высоких частот передаваемого сигнала.

Далее, необходимо считаться с ограниченной чувствительностью датчиков положения в реальных следящих электроприводах, что подробнее рассмотрено ниже.