Пример настройки одноконтурной системы регулирования положения

В случаях, когда двигатели, применяющиеся в следящих электроприводах, допускают прямое включение на полное напряжение источника питания, не требуется ограничивать с помощью схемы управления максимальные значения тока якоря и скорости вращения двигателя. Это позволяет применить для следящего электропривода наиболее простую  одноконтурную систему регулирования с последовательным корректирующим устройством. Оценку возможностей такой структуры выполним, воспользовавшись экспериментальными частотными характеристиками конкретного электропривода. При этом обратим внимание на изучение тех реальных факторов, которые в каждом конкретном случае необходимо преодолеть, чтобы достигнуть заданных динамических показателей.

В качестве примера был взят типовой следящий электропривод, в котором конструкторами были предусмотрены общепринятые меры, направленные на достижение наилучших динамических показателей [24]: малоинерционный двигатель с гладким якорем, безынерционный транзисторный широтно-импульсный преобразователь в цепи якоря, передаточное число редуктора, создающее примерное равенство приведенных моментов инерции двигателя и рабочего механизма. Здесь рабочий механизм РМ с моментом инерции J_РМ = 8 кгм² приводится через редуктор с передаточным числом i = 343 от электродвигателя постоянного тока (Р_Н = 180 Вт, U_Н = 27 В, I_Н = 15 А, n_Н = 3000 об/мин, J_Я = 0,46·10^4 кгм²). Широтно-импульсный преобразователь (ШИП) управляется с помощью регулятора положения, на входе которого суммируются сигнал задания и встречный сигнал с выхода датчика положения вала РМ.

Экспериментальные логарифмические частотные характеристики (ЛЧХ) разомкнутого контура регулирования положения (КРП) РМ анализировались сначала в диапазоне низких частот, а потом  в районе средних и высоких.

Низкочастотным участком амплитудной ЛЧХ разомкнутого КРП определяются такие точностные показатели электропривода, как добротность по скорости и добротность по ускорению, весьма актуальные в электроприводах станков с числовым программным управлением [17], а также в режимах наведения специальных следящих электроприводов [12, 24].

Чтобы повысить точность замкнутой системы регулирования как по задающему сигналу, так и при воздействии возмущений, необходимо в низкочастотной зоне амплитудной ЛЧХ разомкнутой системы регулирования иметь максимально высокий динамический коэффициент усиления. Между тем, в реальном электроприводе амплитудная ЛЧХ разомкнутого КРП имела весьма низкий динамический коэффициент усиления при малых частотах (кривая L₁ на рис. 7.14). Более того, характер её наклона ближе к нулевому (гори­зонтальному), а не к единичному, как это бывает в обыч­ной линейной сис­теме с пропорцио­нальным регуля­тором положения из-за существо­ва­ния интегральной связи между поло­жением и угловой скоростью выход­ного вала РМ. Фазовая же ЛЧХ разомкнутого КРП имеет при низких частотах отстаю­щий фазовый сдвиг, близкий к 90 (кривая ₁ на рис. 7.14), что требует объяснения, так как в рамках линейных систем с минималь­нофазовыми звеньями существует общеизвестная [25, 26] однозначная и отличающаяся от упомянутых кривых зависимость между наклоном амплитудной ЛЧХ системы регулирования и её фазовой характеристикой: так, нулевому наклону амплитудной ЛЧХ соответствует фазовая характеристика, близкая к нулю, единичному её наклону  фазовая характеристика, близкая к 90 и т.д.

Чтобы выявить причины, вызывающие указанный характер ЛЧХ прямого канала следящего электропривода, и объяснить механизм их влияния, структурная схема неизменяемой части системы (вход  напряжение управления U_У на входе ШИП, выход  угол поворота вала РМ ) была представлена последовательным соединением звеньев с промежуточными координатами: n₁  скоростью вала электродвигателя и n₂  скоростью выходного вала РМ. При этом ЛЧХ прямого канала контура регулирования положения определялась для нескольких значений амплитуды пробного сигнала U_У.

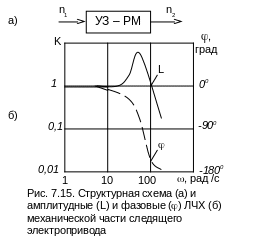Было обнаружено, что ЛЧХ выходного звена, учитывающего динамические свойст­ва инерционных вра­ща­ю­щихся масс РМ, соединенных с валом электродвигателя че­рез механическую пе­ре­дачу (вход  скорость n₁ , выход  скорость n₂), не зависят от амплитуды входного сигнала U_У и довольно точно описываются линей­ным колебательным звеном (рис. 7.15) с частотой резонанса ₁ = 60 рад/с и вы­сотой резонансного мак­­симума А_Р = А_МАКС / А₀ = 5. Здесь А₀ и А_МАКС  значения амплитудной харак­те­ристики звена при ну­ле­вой частоте и часто­те резонанса.

Амплитудные же характеристики перво­го звена (вход  U_У, выход  n₁ на рис. 7.16) требуют более подробных пояснений. Во-первых, в районе  = 60 рад/с наблюдается провал в амплитудной ЛЧХ. Причину его появления следует объяснить влиянием второй массы на движение первой в двухмассовой упругой системе, когда в режиме механического резонанса резко увеличиваются нагрузки на валу двигателя, необходимые для поддержания с возросшей амплитудой периодических движений второй массы. А это в силу естественной мягкости механической характеристики двигателя приводит к снижению его скорости по отношению к сигналу задания и соответствующему напряжению на якоре. Это обстоятельство общеизвестно и описано в публикациях по электроприводам с упругими звеньями [15].

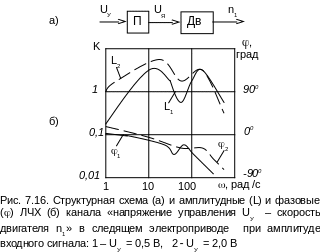Во-вторых, в районе низких частот нарушается однозначная, характерная для минимально-фазовых систем взаимосвязь амплитудной и фазовой ЛЧХ, а вид этих характеристик зависит от амплитуды входного сигнала. Так, при малых сигналах (кривая L₁ на рис. 7.16) снижение амплитудной ЛЧХ при уменьшении частоты пробного синусоидального сигнала наблюдается и в большем диапазоне частот и выражено более явственно, чем при больших (кривая L₂).

Отмеченные особенности амплитудной ЛЧХ неизменяемой части системы при малых частотах следует объяснить наличием сил сухого трения, воздействующих на якорь двигателя. Падающий характер амплитудных ЛЧХ при уменьшении частоты пробного сигнала объясняется снижением доли динамического момента двигателя в доле общего электромагнитного момента при постоянстве величины момента, обусловленного силами сухого трения. По этой же причине при меньших сигналах управления снижение амплитудной характеристики наблюдается в большем диапазоне частот.

Момент, необходимый для преодоления сил трогания электродвигателя, в несколько раз превышает его момент холостого хода и в электродвигателях постоянного тока мощностью 100...400 Вт может доходить до 25...40% от номинального значения. Того же порядка бывает и величина момента от дополнительных сил трения в механических люфтовыбирающих устройствах при предварительной закрутке их торсиона на один-два зуба разрезной шестерни, установленной в последней ступени редуктора или в открытой паре после него. Момент же от сил трения в зубчатых зацеплениях и опорах осей промежуточных ступеней редуктора, не содержащих люфтовыбирающих устройств, оказывается существенно (в 10...20 раз) меньше.

Ослабить неблагоприятное влияние сил сухого трения на вид амплитудной характеристики (а следовательно, и на показатели точности следящего электропривода) можно, охватив это возмущение, например, местной отрицательной обратной связью по скорости электродвигателя. При этом подавление возмущения от сил сухого трения будет тем эффективнее, чем выше быстродействие и точность регулирования в этом контуре. В следящих электроприводах с малоинерционными двигателями (например, с гладким якорем ) можно добиться частоты среза в контуре регулирования скорости n₁ до 300...400 рад/с, что делает электропривод малочувствительным к влиянию сил сухого трения. Экспериментальные ЛЧХ замкнутого контура регулирования скорости n₁ (рис. 7.17) подтверждают сказанное: наблюдаемого на предыдущих характеристиках снижения амплитуды выходного сигнала в районе низких частот нет. Оказывается также подавленным влияние второй массы РМ на характер движения первой (хотя при снятии частотных характеристик вал РМ оставался присоединен­ным через механическую передачу к выходному валу двигателя) и нет поэтому наблюдавшегося ранее провала на амплитудной характерис­тике в районе частоты резонанса. Это происхо­дит потому, что частота среза контура регулирова­ния скорости n₁ оказалась существенно выше часто­ты резонанса в механи­ческой системе.

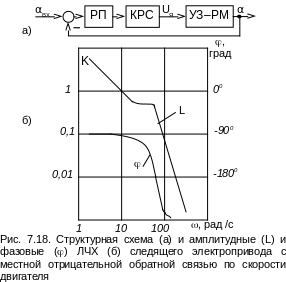
Результирующая ЛЧХ разомкнутого контура регулирования положения РМ с внутренним кон­туром регулирования ско­ро­­сти двигателя n₁ (рис. 7.18) подтверждает возмо­жность восстановления еди­ничного наклона изме­не­ния её амплитуды в районе низких частот и, следовательно, повыше­ния статической точности регулирования. Однако, предельное значение её частоты среза остается сравнительно невысоким (не выше  = 10 рад/с), что объясняется влиянием резонансного максимума, истощающего запас устой­чивости по модулю в системе регулирования.

Ослабить влияние резонансного максимума механической системы на динамические показатели контура регулирования положения РМ можно двумя способами: или соответствующим образом выбрать параметры силового оборудования в электроприводе, или перейти к многоконтурной системе регулирования. Оба варианта рассмотрены ниже.

7.5. Выбор параметров силового оборудования из условия достижения

максимальной точности слежения

Методы оптимизации силового электрооборудования

в следящих электроприводах

Традиционные методики выбора мощности электродвигателей общепромышленных установок обычно исходят из известных нагрузочных диаграмм электропривода и ограничиваются лишь допустимыми условиями использования двигателя по нагреву, по перегрузочному моменту, по максимальной скорости и др. [15, 31].

Для следящих электроприводов задача выглядит сложнее из-за существенного влияния динамических показателей двигателя на качество процессов в электроприводе и в большинстве случаев ее решение неоднозначно. Поэтому процедура выбора силового оборудования сопровождается оптимизацией его по каким-либо критериям, которые позволяют получить наилучшие качественные показатели электропривода при работе в определенных режимах.

Чаще задачу параметрической оптимизации силового оборудования решали для позиционных электроприводов, принимая за критерий оптимизации время перемещения рабочего механизма из одной точки в другую. На наш взгляд, впервые эту задачу в 30-е годы решил Н.А. Тищенко для электропривода летучих ножниц прокатных станов. При этом он исходил из минимума «живой силы» (по терминологии тех лет – запаса кинетической энергии вращающихся масс электропривода) и пришел к общеизвестному на сегодняшний день соотношению для оптимального передаточного числа редуктора

i = (J_РМ / J_Д ) ^0,5,

где J_РМ и J_Д – моменты инерции вращающихся частей рабочего механизма и якоря двигателя.

Позднее это соотношение подтверждалось в работах других авторов, например, для кузнечно-прессового [11], металлургического [1], машиностроительного [2, 17] электрооборудования.

Для следящих электроприводов характерно большее разнообразие режимов работы и требований к ним, чем для позиционных. При этом режим работы электропривода в значительной мере произволен и тогда требуемые мощность двигателя и передаточное число редуктора определяются на основании или максимальной скорости и ускорения [12, 24], или статистических характеристик приложенной нагрузки[12, 22]. Подробный обзор вариантов и примеры оптимизации силовой части электропривода по разным обобщенным показателям выполнил В.Г. Каган [14].

Общим для всех указанных методик является рассмотрение механической системы как абсолютно жесткой. Между тем, наличие податливостей в механической передаче затрудняет достижение высоких точностных показателей в следящем электроприводе.

Наиболее глубоко и убедительно задачу выбора силового оборудования следящих электроприводов с учетом упругостей в механической передаче решил В.М. Терехов [28, 29]. Взяв за критерий оптимизации точность слежения электропривода, он сформулировал основные этапы оптимизации, нашел эффективные алгоритмы выделения и определения величин параметров конструкции, в наибольшей степени влияющих на точность.

Приведенный краткий обзор указывает на важность умения правильно выбирать параметры силового оборудования, так чтобы добиться максимальной точности слежения, когда этому препятствует наличие податливостей в механической передаче.