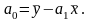- •Предмет та метод економетрики.
- •3.Математична модель та основні етапи її побудови.
- •Теоретичні основи математичного моделювання та класифікація моделей.
- •5. Регресійна та економетрична модель.
- •Знаходження статистичних оцінок параметрів методом найменших квадратів (мнк) через систему нормальних рівнянь.
- •Знаходження статистичних оцінок параметрів методом найменших квадратів (мнк) через прирости.
- •Стандартна похибка оцінки за рівнянням економетричної моделі.
- •9.Коефіцієнт детермінації та коефіцієнт кореляції.
- •10. Основні припущення при використанні мнк.
- •Незміщеність і ефективність оцінок мнк.
- •12.Перевірка нульових гіпотез.
- •13.Побудова інтервалів довір’я рівняння економетричної моделі.
- •14.Перевірка нульових гіпотез і довірчі інтервали параметрів і .
- •15.Перевірка моделі на адекватність.
- •16. Криві зростання.
- •17. Зведення деяких нелінійних моделей до лінійних. (Приклади використання нелінійних моделей на практиці)
- •18. Лінійна багатофакторна економетрична модель. Мнк для багатофакторної економетричної моделі
- •19. Лінійна економетрична модель з трьома змінними. Мнк для моделі з трьома змінними
- •Методи виявлення гетероскедастичності. (Декілька питань по різних тестах)
- •Узагальнений мнк.
- •Природа автокореляції та її вплив в економетричних моделях.
- •34. Методи знаходження оцінок в умовах автокореляції.
5. Регресійна та економетрична модель.
Побудова економетричних моделей базується на технології моделювання, яка характерна для здійснення регресійного аналізу. Регресія починається там, де є ряд спостережень над досліджуваними величинами
Y y1 y2 ... yn
X x1 x2 ... xn
- який є рядом даних, а x і y - випадкові величини, при цьому xi, yi - їх
практичні реалізації або можливі значення, n - кількість спостережень.
При вимірюванні кількісних ознак можуть бути отримані два типи рядів
даних - динамічні та варіаційні.
Динамічний ряд - це послідовність спостережень за процесом або
явищем у рівновіддалені проміжки часу. Якщо xi - значення деякої ознаки
економічного процесу в i -й проміжок часу, то динамічний ряд x1, x2 ,…,
xi ,…, xn можна отримати, вимірюючи значення цієї ознаки в рівновіддалені
проміжки часу.
Варіаційні ряди - це ряди даних, які показують кількісну міру певної
ознаки у всіх об’єктів однієї сукупності, наприклад, оцінки за екзамен студентів
однієї групи.
Першим кроком до побудови регресійної моделі є ідентифікація змінних. Треба визначити яка із спостережуваних величин є ознакою (залежною величиною, пояснюваною змінною, функцією), а які величини є незалежними (аргументами, пояснюючими змінними, факторами).
Другим етапом до побудови регресійної моделі є специфікація моделі, а саме: на основі даних ряду досліду потрібно визначити аналітичну форму
зв'язку (1.1).
Найчастіше специфікацію проводять з допомогою хмарки точок (діаграми
розсіювання). На осі абсцис відзначають значення незалежної змінної ( x ), на
осі ординат - значення залежної змінної ( y ).
За виглядом діаграми розсіювання можна висунути гіпотезу про
лінійність чи нелінійність зв’язку між змінними.
ІІІ-й етап - оцінка параметрів моделі.
ІV-й - аналіз моделі по залишках.
Припустимо, що в результаті специфікації ми переконалися, що залежність між y та x - лінійна, тоді (1.1) набере вигляду: y = a + bx + u (1.2)
де:a , b - невідомі детерміновані параметри; y - вектор спостережень за
залежною змінною, { } y = y1, y2 ,..., yn ; x - вектор спостережень за незалежною
змінною, { } x = x1, x2 ,..., xn ; u - випадкова складова, збурення, { } u = u1,u2 ,...,un .Рівняння регресії (1.2) - називається економетричною моделлю, якщо у та х є кількісними показниками деяких економічних явищ чи процесів. Таким чином, рівняння регресії перетворюється в економетричне, якщо воно налагоджує зв'язок між кількісними показниками об'єктів економіки.
Знаходження статистичних оцінок параметрів методом найменших квадратів (мнк) через систему нормальних рівнянь.
Цей метод є найточнішим методом знаходження статистичних оцінок параметрів економетричної моделі. Через хмарку точок діаграми розсіювання можна провести безліч прямих. В даному випадку завдання дослідника знайти оціночне рівняння: уоцін.=а0+а1х. Згідно МНК пряма повинна пройти так, щоб сума квадратів залишків була мінімальною. Тобто ідея МНК полягає в побудові цільової функції, яка мінімізує суму квадратів відхилень: uі=уі-уіоцін.
Згідно
критерію для всіх сукупностей точок:

Щоб дослідити ф-цію двох змінних на min, потрібно знайти їх часткові похідні і прирівняти до нуля:

2 ∑(уі-
а0-а1хі)*(-1)=0 ∑
а0+∑
а1хі=∑уі
∑(уі-
а0-а1хі)*(-1)=0 ∑
а0+∑
а1хі=∑уі
2∑(уі- а0-а1хі)*(-х)=0 ∑ а0 хі+∑ а1хі2=∑ хі уі

Дана с-ма р-нь назив с-мою нормальних р-нь. Розв’язавши яку можна знайти параметри а0 та а1.
 ;
;