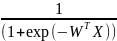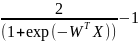1. Фазификация фактических данных, т.е. точное значение x₀ интерпретируется как нечеткая точка.

2. Композиция входной переменной и условной части правила: х₀ ° Ai, y₀ ° Bi, т. е. вычисляется уровень пригодности правила к ситуации. Если факт задан нечеткой точкой, то композиция сводится к выявлению соответствующей степени принадлежности.

3. Вычисление нечеткой импликации:

(х₀ ° Ai) ^ (y₀ ° Bi) → С_i для любого R.

Результатом выполнения п. 2 и 3 для всех правил являются N нечетких значений для выхода Z.

4. Агрегация среднего значения:

т.е. построение нечеткого значения выхода по результатам предыдущих этапов.

5. Дефазификация, т. е. выбор представляющего элемента но агрегированному нечеткому понятию.

Схемы нечеткого вывод у разных авторов уточняются до оператора нечеткой импликации. Распространены 5 схем нечеткого вывода:

1. По Мамдани: импликация моделируется минимумом, агрегация – максимумом

2. По Цукамото: для монотонных функций принадлежности. L₁', L₂' – уровни достоверности применения правил; z₁,z₂ – значения выходной переменной по первому и второму правилу:

z₁ = C₁^-1( L₁) , z₂ =C₂^-1( L₂)

z = (L₁'* z₁ +L₂'* z₂)/( L₁'+ L₂')

Ввиду монотонности функций вычисления выходной переменной сводят к усреднению значений, полученных по разным правилам.

3. По Суджено: правые части правил вывода ограничиваются линейным случаем

Если х – А₁ и у – В₁, тогда z = a₁x + b₁y

4. По Ларсену: импликация выполняется с помощью произведения.

5. Упрощенная схема: Если х – А_i и у – В_i, тогда z = Z_i, где z – четкое значение.

Поскольку правые части правил в упрощенной схеме задаются четко, то в результате вывода получается дискретное множество решений для каждого элемента, у которого задана определенная степень уверенности. В качестве выходной переменной выбирается значение с максимальной уверенностью.

5. Архитектура нечёткой экспертной системы

См. вопрос 3

6. Искусственная нейронная сеть. Математическая модель нейрона.

Искусственные нейронные сети представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как совокупность (сеть) отдельных структур (нейронов).

Биологический нейрон характеризуется наличием тела, входов, выходов и места их соединения:

1. Сома – тело,

2. Дендриты – дерево входов.

3. Аксоны – дерево выходов.

4. Синапсы – место соединения дендритов и аксонов. Синапсы имеют переменное сопротивление для переходных сигналов.

Принятые синапсами сигналы либо возбуждают нейрон, либо его тормозят в зависимости от порогового значения. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синаптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. Дендрит имеет собственный приоритет, который он меняет в течение жизни.

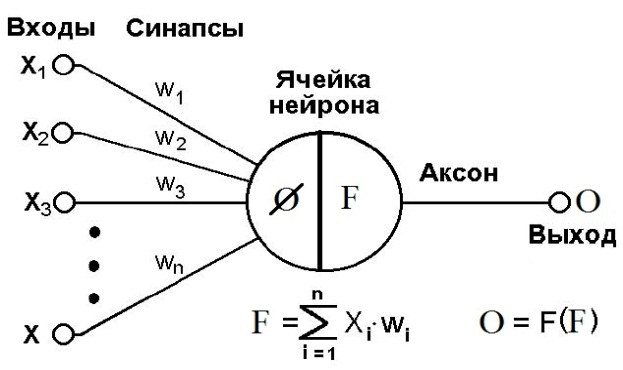
Рисунок 2 Искусственный нейрон

Схема будущего элемента – взвешенный пороговый сумматор.

Биологический нейрон является взвешенным пороговым сумматором.

Математически нейрон характеризуется следующими параметрами:

1. Вектор входов

2. Вектор выходов

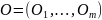
3. Вектор весов

4. Порог срабатывания ø

5. Функция активации F

Наиболее часто используемые функции активации

Название функции	Формула
Линейная
Функция «знак»
Униполярная сигмоидальная
Биполярная сигмоида
Гиперболический тангенс