1. Визначення

Нехай дана функція   і   - Внутрішня точка області визначення f. Тоді

• x ₀ називається точкою локального максимуму функції f, якщо існує проколота околиця   така, що

• x ₀ називається точкою локального мінімуму функції f, якщо існує проколота околиця   така, що

Якщо нерівності вище строгі, то x ₀ називається точкою строгого локального максимуму або мінімуму відповідно.

• x ₀ називається точкою абсолютного (глобального) максимуму, якщо

• x ₀ називається точкою абсолютного мінімуму, якщо

Значення функції f (x ₀₎ називають (суворим) (локальними) максимумом або мінімумом в залежності від ситуації. Точки, які є точками (локального) максимуму або мінімуму, називаються точками (локального) екстремуму.

2. Зауваження

Функція f, визначена на множині M, може не мати на ньому жодного локального або абсолютного екстремуму. Наприклад, 

3. Необхідні умови існування локальних екстремумів

• Лемма Ферма. Нехай функція 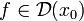  дифференцируема в точці локального екстремуму x _0. Тоді:

 .

• Якщо в точці екстремуму існує перша приватна похідна (з якого-небудь аргументу), то вона дорівнює нулю.

4. Достатні умови існування локальних екстремумів

• Нехай функція 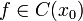  неперервна в 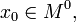  і існують кінцеві або безкінечні односторонні похідні   . Тоді за умови

x ₀ є точкою строгого локального максимуму. А якщо

то x ₀ є точкою строгого локального мінімуму.

Зауважимо, що при цьому функція не дифференцируема в точці x ₀

• Нехай функція f неперервна і двічі диференційована в точці x ₀ . Тоді за умови

 і 

x ₀ є точкою локального максимуму. А якщо

 і 

то x ₀ є точкою локального мінімуму.

16. . Опуклість і вгнутість кривих. Точка перегину             Нехай крива задана рівнянням , де  - неперервна функція, що має неперервну похідну  на деякому проміжку . Тоді в кожній точці такої кривої можна провести дотичну (ці криві ще називають гладкими кривими). Візьмемо на кривій довільну точку , де , .             Означення. Якщо існує окіл точки такий, що для всіх  відповідні точки кривої лежать над дотичною, проведеною до кривої в  точці , то крива в точці називається вгнутою догори (рис. 6.15).             Означення. Якщо існує окіл точки  такий, що для всіх  відповідні точки кривої лежать під дотичною, проведеною до кривої в точці , то крива в точці  називається вгнутою донизу (рис. 6.16).             Означення. Точка називається точкою перегину кривої, якщо існує окіл точки  - такий, що для всіх  крива вгнута по один бік, а для всіх  - по другий бік (рис. 6.17,  6.18).              Рис.6.15.                                           Рис.6.16             Якщо крива, задана рівнянням  в кожній точці деякого проміжку вгнута догори, її називають вгнутою на цьому проміжку; якщо крива в кожній точці проміжку вгнута донизу, її називають опуклою на даному проміжку. Не всяка крива має точку перегину. Так, криві, зображені на рис. 6.21, 6.22, точок перегину не мають. Іноді крива може мати тільки одну, а іноді кілька точок перегину, навіть нескінченну множину. Поставимо задачу: знайти точки вгнутості кривої та точки перегину, якщо вони існують. Для цього доведемо теорему.             Теорема. Нехай крива задана рівнянням  і нехай існує окіл  точки такий, що функція     Рис.6.17               Рис.6.18          Рис.6.19           Рис.6.20  при кожному має похідні до другого порядку включно, причому  в точці є неперервною функцією. Тоді, якщо , то крива в точці  вгнута догори. Якщо , то крива в точці вгнута донизу. З теореми випливає, що коли крива задана рівнянням , де - визначена і має неперервні похідні до другого порядку включно на деякому проміжку , і в кожній точці цього проміжку, то задана крива на цьому проміжку вгнута. Якщо , то задана крива на цьому проміжку опукла. Інакше, якщо  при , то крива не має точок перегину. Отже точка  може бути точкою перегину кривої, заданої рівнянням , якщо  або в точці  не існує, але  існує. Надалі розглядатимемо випадок, коли  існує в усіх точках проміжку . Тоді корені рівняння можуть бути абсцисами точок перегину кривої. Те, що похідна другого порядку дорівнює в даній точці нулю, є тільки необхідною умовою того, щоб   була абсцисою точки перегину кривої, але не достатньою.             Для того, щоб знайти точки перегину кривої, заданої рівнянням , треба: 1) визначити від функції  похідну другого порядку  і прирівняти її до нуля . З коренів цього рівняння вибрати тільки дійсні корені і ті, які належать області існування функції; 2) в околі кожного вибраного таким чином кореня визначити знак похідної другого порядку  спочатку при значеннях , менших від розглядуваного кореня, а потім при значеннях , більших за даний корінь. Якщо при переході  через вибраний корінь  похідна  змінює знак, то точка  є точкою перегину заданої кривої. Якщо при переході  через  знак похідної другого порядку не змінюється, то  не є точкою перегину кривої. Зокрема, якщо при переході через  змінює знак “+” на “-”, то  крива при проходженні через точку перегину змінює відповідно свій вигляд із вгнутості на опуклість. Якщо  при переході через  змінює знак   “-” на “+” , то крива  при проходженні через точку перегину  змінює відповідно свій вигляд з опуклості на вгнутість. Приклад.        Знайти інтервали вгнутості й опуклості та точки перегину кривої, заданої рівнянням .             Р о з в ’ я з о к. Знаходимо похідні першого та другого порядків: ; .             Прирівнюємо  до нуля. Дістанемо рівняння , звідки знаходимо корені             Отже, в інтервалах  похідна , а в інтервалі  похідна . Тому в інтервалах  крива вгнута, а в інтервалі - опукла. Точки  є точки перегину кривої.

• 17. Асимптота ^[1] (від греч. ασϋμπτωτος - Неспівпадаючі, не стосується) кривої с нескінченної гілкою - пряма, що володіє тим властивістю, що відстань від точки кривої цієї до прямий прагне до нуля при видаленні точки вздовж гілки в нескінченність ^[2]. Термін вперше з'явився у Аполлонія Пергського, хоча асимптоти гіперболи досліджував ще Архімед ^[3].

Для гіперболи   асимптотами є осіабсцис і ординат. Крива може наближатися до своєї асимптоти, залишаючись з одного боку від неї	Загасаючі коливання.   . Крива може нескінченну кількість разів перетинати асимптоту
Приклад асимптоти для кривої в просторі. Спіраль нескінченно наближається до прямої

1. Види асимптот графіків

1.1. Вертикальна

Вертикальна асимптота - пряма виду   за умови існування межі   .

Як правило, при визначенні вертикальної асимптоти шукають чимало межа, а два односторонніх (лівий і правий). Це робиться з метою визначити, як функція веде себе по мірі наближення до вертикальної асимптоти із різних сторін. Наприклад:

1. 

2. 

Зауваження: зверніть увагу на знаки бесконечностей в цих равенствах.

1.2. Горизонтальна

Горизонтальна асимптота - пряма виду   за умови існування межі

 .

1.3. Похила

Похила асимптота - пряма виду   за умови існування меж

Приклад похилій асимптоти

1. 

2. 

Зауваження: функція може мати не більше двох похилих (горизонтальних) асимптот!

Зауваження: Якщо хоча б один з двох згаданих вище меж не існує (або рівний   ), То похилій асимптоти при   (Або   ) Не існує!

Зв'язок між похилій і горизонтальній асимптотами

Якщо при обчисленні межі   , То очевидно, що похила асимптота збігається з горизонтальною. Яка ж зв'язок між цими двома видами асимптот?

Справа в тому, що горизонтальна асимптота є окремим випадком похилої при   , І з вище зазначених зауважень випливає, що

1. Функція має або тільки одну похилу асимптоту, або одну горизонтальну асимптоту, або одну похилу і одну горизонтальну, або дві похилих, або дві горизонтальні, або ж зовсім не має асимптот.

2. Існування зазначених у п. 1.) Асимптот безпосередньо пов'язано з існуванням відповідних меж.

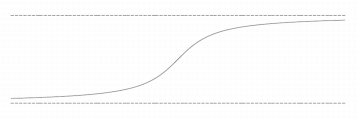
Графік функції з двома горизонтальними асимптотами

2. Знаходження асимптот

2.1. Порядок знаходження асимптот

1. Знаходження вертикальних асимптот.

2. Знаходження двох меж 

3. Знаходження двох меж   :

якщо   в п. 2)., то   І межа   шукається за формулою горизонтальної асимптоти,   .

2.2. Похила асимптота - виділення цілої частини

Також похилу асимптоту можна знайти, виділивши цілу частину. Наприклад:

Дана функція   .

Розділивши чисельник націло на знаменник, отримаємо:

 .

При   ,   ; Цебто:

 ,

і   є шуканим рівнянням асимптоти.

18. 1)Первісна

Первообразной ^[1] або примітивною функцією (іноді називають також антіпроізводной) даної функції f називають таку F, похідна якої (на всій області визначення) дорівнює f, тобто F '= f. Обчислення первообразной полягає в знаходженні невизначеного інтеграла, а сам процес називається інтегруванням.

Так, наприклад, функція   є первообразной   . Так як похідна константи дорівнює нулю,   матиме нескінченне кількість первісних; таких як   або   ... і т. д. ; Таким чином сімейство первісних функції x ² можна позначити як F (x) = x ³ / 3 + ​​C , Де C - будь-яке число.Графіки таких первісних зміщені вертикально відносно один одного, і їх положення залежить від значення C.

Первісні важливі тим, що дозволяють обчислювати інтеграли. Якщо F - первообразная інтегрованої функції f, то:

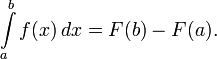
Це співвідношення називається формулою Ньютона - Лейбніца.

Завдяки цьому зв'язку безліч первісних даної функції f називають невизначеним інтегралом (загальним інтегралом) f і записують у вигляді інтеграла без вказівки меж:

Якщо F - первообразная f, і функція f визначена на якомусь інтервалі, тоді кожна наступна первообразная G відрізняється від F на константу: завжди існує числоC, таке що G (x) = F (x) + C для всіх x. Число C називають постійної інтегрування.

Кожна безперервна функція f має первісну F, одна з яких представляється у вигляді інтеграла від f із змінною верхньою межею:

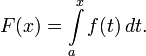
Також існують не безперервні (розривні) функції, які мають первісну. Наприклад,   з f (0) = 0 не безперервно при x = 0 , Але має первісну   з F (0) = 0 .

Деякі первісні, навіть незважаючи на те, що вони існують, не можуть бути виражені через елементарні функції (такі як многочлени, експоненціальні функції,логарифми, тригонометричні функції, зворотні тригонометричні функції та їх комбінації). Наприклад:

Більш розгорнутий виклад цих фактів див диференціальної теорії Галуа.