3.2. Відношення нескінченно великих

Доведемо теорему для невизначеностей виду   .

Нехай, для початку, границя відношення похідних кінцевий і дорівнює A . Тоді, при прагненні x до a праворуч, це відношення можна записати як A + α , Де α -O (1). Запишемо це умова:

 .

Зафіксуємо t з відрізка   і застосуємо теорему Коші до всіх x з відрізка   :

 , Що можна привести до наступного вигляду:

 .

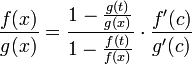Для x , Досить близьких до a , Вираз має сенс; межа першого множника правої частини дорівнює одиниці (оскільки f (t) і g (t) - константи, а f (x) і g (x) прагнуть до нескінченності). Значить, цей множник дорівнює 1 + β , Де β - Нескінченно мала функція при прагненні x до a справа. Випишемо визначення цього факту, використовуючи те ж значення ε , Що і у визначенні для α :

 .

Отримали, що відношення функцій представимо у вигляді (1 + β) (A + α) , І 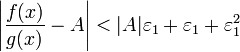  . По любому даному ε можна знайти таке ε ₁ , Щоб модуль різниці відносини функцій і A був менше ε , Значить, межа відносини функцій дійсно дорівнює A .

Якщо ж межа A нескінченний (припустимо, він дорівнює плюс нескінченності), то

 .

У визначенні β братимемо   ; Перший множник правої частини буде більше 1 / 2 при x , Досить близьких до a , А тоді   .

Для інших баз докази аналогічні наведеним.

4. Приклади

• 

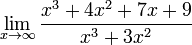• Тут можна застосувати правило Лопіталя 3 рази, а можна поступити інакше. Потрібно розділити і чисельник, і знаменник на x найбільшою мірою (у нашому випадку x ³ ). У цьому прикладі виходить:

•  ;

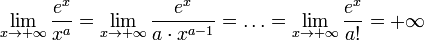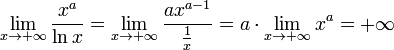•  при a> 0 .

Модуль 2

15.1) Зростання та спадання функції

Дослідження функції на зростання та спадання ґрунтується на теоремі математичного аналізу.

Теорема. Нехай функція неперервна на проміжку <a,б> і диференційована в інтервалі (а,б).для того, щоб функція f була зростаючою(спадною) на проміжку <a,б>, необхідно і достатньо виконання двох умов:

1.

2. рівність не повинна виконуватися ні в жодному інтервалі, що міститься в <a,б>.

Як наслідок цієї теореми можна використовувати таку теорему (достатня ознака строгої монотонності):

Теорема. Нехай функція f неперервна на проміжку <a,б> і диференційована в інтервалі (а,б). Якщо , то f зростає(спадає) на <a,б>.

Тому для знаходження проміжків зростання та спадання диференційованої функції діють у такий спосіб:

1. Знаходять:

а)область визначення функції , якщо вона наперед не задана;

б)похідну даної функції ;

в)точки, в яких похідна дорівнює нулю, для чого розв'язують рівняння , а також точки, в яких функція визначена, але похідна не існує, їх називають критичними точками.

2. Визначають знак похідної на конкретному інтервалі, достатньо обчислити її значення для будь-якого значення аргументу, що належить цьому інтервалу.

2) Екстремум ( лат. extremum - Крайній) в математиці - максимальне або мінімальне значення функції на заданому безлічі. Точка, в якій досягається екстремум, називається точкою екстремуму. Відповідно, якщо досягається мінімум - точка екстремуму називається точкою мінімуму, а якщо максимум - точкою максимуму. В математичному аналізі виділяють також поняття локальний екстремум (відповідно мінімум або максимум).