4 Похідна складеної функції. Повна похідна. Інваріантність форми повного диференціала

Нехай - функція двох змінних та , кожна з яких, у свою чергу, є функцією незалежної змінної :

тоді функція є складеною функцією змінної .

Теорема. Якщо функції диференційовні в точці , а функція диференційовна в точці , то складена функція також диференційовна в точці . Похідну цієї функції знаходять за формулою

. (10)

Доведення

За умовою теореми ,

де та при,.

Поділимо на і перейдемо до границі при:

Аналогічно знаходять похідну, якщо число проміжних змінних більше двох. Наприклад, якщо , де , то

. (11)

Зокрема, якщо, а, то

,

а оскільки , то

. (12)

Цю формулу називають формулою для обчислення повної похідної  (на відміну від частинної похідної).

Розглянемо загальніший випадок. Нехай - функція двох змінних та, які, в свою чергу, залежать від змінних :, , тоді функція є складеною функцією незалежних змінних та, а змінні та - проміжні.

Аналогічно попередній теоремі доводиться таке твердження.

Якщо функції та диференційовні в точці , а функція диференційовна в точці , то складена функція диференційовна в точці і її частинні похідні знаходяться за формулами:

; . (13)

Формули (13) можна узагальнити на випадок більшого числа змінних. Якщо, де, то

Знайдемо диференціал складеної функції. Скориставшись формулами (13), отримаємо

Отже, диференціал функції, де , , визначається формулою

, (14)

де

.

Порівнявши формули (14) і (4) дійдемо висновку, що повний диференціал функції має інваріантну (незмінну) форму незалежно від того, чи є x та незалежними змінними, чи диференційовними функціями змінних u та v. Проте формули (4) і (14) однакові лише за формою, а по суті різні, бо у формулі (4) і- диференціали незалежних змінних, а у формулі (14) і- повні диференціали функцій та .

Диференціали вищих порядків властивості інваріантності не мають. Наприклад, якщо, де , , то

(15)

Формула (15) відрізняється від формули (8), оскільки для складеної функції диференціали та можуть і не дорівнювати нулю. Отже, для складеної функції, де , , формула (8) неправильна.

5 Диференціювання неявної функції

Нехай задано рівняння

, (16)

де - функція двох змінних.

Нагадаємо, що коли кожному значенню x з деякої множини відповідає єдине значення, яке разом з x задовольняє рівняння (16), то кажуть, що це рівняння задає на множині неявну функцію.

Таким чином, для неявної функції, заданої рівнянням (16), має місце тотожність

.

Які ж умови має задовольняти функція щоб рівняння (16) визначало неявну функцію і при тому єдину? Відповідь на це запитання дає така теорема існування неявної функції [8].

Теорема. Нехай функція і її похідні та визначені та неперервні у будь-якому околі точки і , а; тоді існує окіл точки , в якому рівняння визначає єдину неявну функцію, неперервну та диференційовну в околі точки і таку, що .

Знайдемо похідну неявної функції. Нехай ліва частина рівняння (16) задовольняє зазначені в теоремі умови, тоді це рівняння задає неявну функцію, для якої на деякій множині точок x має місце тотожність. Оскільки похідна функції, що тотожно дорівнює нулю, також дорівнює нулю, то повна похідна. Але за формулою (12) маємо , тому , звідки

. (17)

За цією формулою знаходять похідну неявної функції однієї змінної.

14. Правило Бернуллі ^[1] -Лопіталя - метод знаходження меж функцій, розкриває невизначеності виду 0 / 0 і   . Обгрунтовує метод теорема стверджує, що за деяких умов межа відносини функцій дорівнює межі відносини їх похідних.

1. Точне формулювання

Умови:

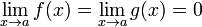1.  або   ;

2.  і   діфференцируєми в проколеної околиці   ;

3.  в проколеної околиці   ;

4. існує   ,

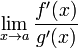тоді існує   .

Межі також можуть бути односторонніми.

2. Історія

Спосіб розкриття такого роду невизначеностей був опублікований в підручнику "Analyse des Infiniment Petits" 1696 за авторством Гійома Лопіталя. Метод був повідомлений Лопиталю в листі його першовідкривачем Іоганном Бернуллі. ^[2]

3. Доказ

3.1. Ставлення нескінченно малих

Доведемо теорему для випадку, коли межі функцій дорівнюють нулю (тобто невизначеність виду   ).

Оскільки ми розглядаємо функції f і g тільки в правій проколеної полуокрестності точки a , Ми можемо безперервним чином їх доопределить в цій точці: нехай f (a) = g (a) = 0 . Візьмемо деякий x з розглянутої полуокрестності і застосуємо до відрізка  теорему Коші. З цієї теореми отримаємо:

 ,

але f (a) = g (a) = 0 , Тому   .

Далі, записавши визначення межі відносини похідних і позначивши останній через A , З отриманого рівності виводимо:

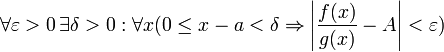 для кінцевого межі і

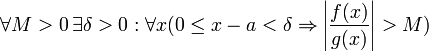 для нескінченного,

що є визначенням меж відносини функцій.