
- •Основні правила диференціювання
- •1) Похідна складеної функції Якщо функція має похідну в точці х, а функція – має похідну в точці , тоді складена функція диференційовна в точці х, причому
- •Якщо неперервна та строго монотонна в деякому околі точки х функція має похідну в цій точці, тоді обернена функція в точці у має похідну, причому
- •2 Диференційованість функції
- •3 Повний диференціал функції та його застосування до обчислення функцій і похибок. Диференціали вищих порядків
- •4 Похідна складеної функції. Повна похідна. Інваріантність форми повного диференціала
- •5 Диференціювання неявної функції
- •3.2. Відношення нескінченно великих
- •4. Приклади
- •15.1) Зростання та спадання функції
- •1. Визначення
- •2. Зауваження
- •3. Необхідні умови існування локальних екстремумів
- •4. Достатні умови існування локальних екстремумів
- •1. Властивості первісної
- •2. Техніка інтегрування
- •3. Інші визначення
- •1. Таблиця основних інтегралів
- •2. Метод розкладання на суму
- •3. Метод підстановки або заміни змінної інтегрування
- •4. Метод інтегрування частинами
- •21. Площадь криволинейной трапеции.
10.1) Застосування диференціалу до наближених обчислень.
Диференціалом функції у = f(х) (або диференціалом першого порядку) називається добуток похідної цієї функції f'(х) на довільний приріст аргументу x:
dy = f'(х) х.
Диференціал аргументу дорівнює приросту аргументу: dx = x. Тому диференціал функції дорівнює добутку її похідної на диференціал аргументу:
dy =f'(x) dx.
Диференціалом другого порядку називається диференціал від диференціала першого порядку:
d2y = f’’(x) dx2,
тобто диференціал другого порядку функції у = f(х) дорівнює добутку другої похідної цієї функції на квадрат диференціала аргументу.
Абсолютна і відносна похибки. Розглянемо функцію у = f(x). Припустимо, що величина х добута безпосереднім вимірюванням або внаслідок наближеного обчислення. Тоді при знаходженні величини х ми припускаємо незалежну від нас похибку x.
Нехай х
— наближене
значення аргументу (вимірюваної
величини), х — абсолютна
похибка величини х, ![]() — відносна
похибка величини х, а х+x
— істинне значення вимірюваної
величини (x
може бути як додатним, так і від'ємним
числом).
— відносна
похибка величини х, а х+x
— істинне значення вимірюваної
величини (x
може бути як додатним, так і від'ємним
числом).
Тоді х визначає наближене значення функції f(х), а. х+x — істинне її значення f(x+x), звідки випливає, що абсолютна похибка функції
|у| = |f(x+x) – f(x) |.
При малих значеннях x (близьких до нуля) величину у можна наближено замінити диференціалом dy.
y = f(x+x) - f(x) » f'(x) dx = dy.
Вигода заміни приросту функції у її диференціалом dy полягає в тому, що dy залежить від x лінійно, а у є складнішою залежністю від x.
Припускаючи, що y » dy, дістанемо вираз для відносної похибки величини у:
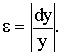
Обчислення наближеного значення приросту функції за допомогою диференціала. Нехай дано функцію y=f'(x); приріст цієї функції у = f(х+х) — f(x), її диференціал dy = f’(x)dx. При досить малих (близьких до нуля) приростах аргументу х вважатимемо, що
y » dy.
тобто, що приріст функції наближено дорівнює її диференціалу.
Обчислення наближеного числового значення функції. Нехай дано функцію y = f(x): приріст цієї функції у = f'(x+x)—f(x), її диференціал dy = f'(x)dx. При досить малих х маємо x » dy. Замінивши приріст функції її диференціалом, дістанемо
ft(x)dx » f(x+x) — f(x),
звідки
f(x+x) » f(x) + f'(х) х.
Застосувавши цю формулу можна значно простіше знайти числове значення функції; геометричне це відповідає заміні ділянки кривої відрізком дотичної.
Наближене обчислення степенів. Розглянемо функцію f(х) = xn. Нехай аргумент х набуває малого приросту х. Обчислимо наближене значення функції f(х+x) = (x+x)n:
f(x+x) » f(x) + f’(x) x.
Маємо:
f(х+x) = (х + x)n; f(x) = xn; f’(х)x = nxn-1x,
звідки
(x+x)n » xn + nxn-1x.
Окремі випадки формули: 1) п = 2, (x+x)2 » x2 + 2xx; 2) п = 3, (х+ Dx)3 » x3 + 3x2x; 3) x = 1, (1 + x)n » 1 + nx.
Наближене
обчислення коренів. Розглянемо
функцію f(х)=![]() Нехай
аргумент х набуває
малого приросту х. Обчислимо
наближене значення функції f(x+x)
=
Нехай
аргумент х набуває
малого приросту х. Обчислимо
наближене значення функції f(x+x)
= ![]() .
Маємо:
.
Маємо:

звідки

Окремі випадки формули:
1)
n = 2, ![]()

3)
x=1, ![]()
Наближене обчислення обернених величин. Розглянемо функцію f(x) = 1/х.
Нехай
аргумент x: набуває малого приросту x.
Обчислимо наближене значення функції
f(x+x)
= ![]() .
Маємо:
.
Маємо:
f(x+x)
= ![]()
звідки
![]()
Окремі випадки формули:
1) x
< 0, ![]()
3)
x=1 i x<0, ![]()
Наближене обчислення синусів і тангенсів малих кутів. Нехай для функції f(x)=sin x аргумент х=0 набуває малого приросту х. Обчислимо наближене значення функції:
f(х+х) = sin(х+x) = sin(0 + x) = sin x.
Застосовуючи формулу для обчислення наближеного значення функції, маємо:
f(х+х) = sinx; f(х) = sin х = sin 0 = 0;
f’(х)x = cosхх = cos 0 · х = x,
звідки
sin х » 0 + х; sin x » x.
Синус малого кута наближено дорівнює самому куту (кут береться в радіанній мірі).
Аналогічно можна показати, що справджується наближена рівність
tgx » x,
тобто тангенс малого кута наближено дорівнює самому куту (кут береться в радіанній мірі).
2)рівняння дотичної та нормалі до графіка функції
Нехай функція у = f (t) означена і неперервна на деякому проміжку [a; b]. Визначимо рівняння дотичної й нормалі до графіка функції у = f (x) у точці з абсцисою .
Оскільки дотична й нормаль проходять через точку з абсцисою х0, то рівняння кожної з них будемо шукати у вигляді рівняння прямої, що проходить через задану точку М0 (х0; у0) у даному напрямі (рис. 4.4):
, (4.2)
де k кутовий коефіцієнт дотичної. Використовуючи геометричний зміст похідної, маємо .
Рис. 4.4
Рівняння дотичної. Оскільки , то з виразу (4.2) ді- станемо рівняння дотичної у вигляді
. (4.3)
Рівняння нормалі. Означення. Нормаллю до графіка функції в точці М0 називається перпендикуляр, проведений до дотичної в цій точці (рис. 4.4).
Використовуючи умову перпендикулярності дотичної та нормалі, знаходимо кутовий коефіцієнт нормалі і записуємо її рівняння у вигляді
. (4.4)
Приклад. Знайти рівняння дотичної та нормалі до графіка функції у = х2 у точці з абсцисою х0 = – 3.
l Знайдемо похідну від заданої функції , звідси .
Рівняння дотичної (4.3) і нормалі (4.4) запишуться так: або у загальному вигляді: 6х + у + + 9 = 0, х – 6у + 57 = 0.
Залежність між неперервністю і диференційовністю функції
Функція у = f (x) є неперервною в точці х, якщо у цій точці .
Означення. Функція у = f (x) називається диференційовною в точці, якщо у цій точці вона має похідну, тобто якщо існує кінцева границя:
.
Означення.Функція у = f (x) називається диференційовною на інтервалі (а; b), якщо вона диференційовна в кожній точці даного інтервалу.
Зв’язок між неперервністю і диференційовністю функції встановлює теорема.
Теорема. Якщо функція диференційовна в деякій точці, то у цій точці функція неперервна.
Обернене твердження неправильне: для неперервної функції може не існувати похідної.
Справді, нехай функція диференційовна в точці . Запишемо тотожність , звідси
Таким чином, функція неперервна в точці .
Рис. 4.5 |
Наслідок. Якщо функція розривна в деякій точці, то вона не має похідної в цій точці.
Прикладом неперервної функції, що не має похідної в одній точці, є функція (рис. 4.5). Ця функція неперервна при х = 0, але не ди- ференційовна для цього значення, оскільки в точці з абсцисою х = 0 не існує дотичної до графіка функції.
Таким чином, необхідною умовою диференційовності функції у = f (х) у точці х є її неперервність у цій точці.
Основні правила диференціювання
Теорема 1. Похідна сталої дорівнює нулю, тобто якщо у = с, де с = const, то .
Теорема 2. Похідна алгебраїчної суми скінченної кількості диференційовних функцій дорівнює алгебраїчній сумі похідних цих функцій: .
Теорема 3. Похідна добутку двох диференційовних функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:
.
Теорема 4. Сталий множник можна виносити за знак похідної:
, де .
Теорема 5. Якщо чисельник і знаменник дробу диференційовні функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різницею добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадратом знаменника початкового дробу .
Зауваження. Похідну від функції , де , зручно обчислювати як похідну від добутку сталої величини на функцію u (x):
.
Приклад. Обчислити похідну для функції у = tg x.
Таким чином, .
Похідна складної функції. Нехай у = f (u), де , тобто . Функція f (u) називається зовнішньою, а функція — внутрішньою, або проміжним аргументом.
Теорема 6. Якщо у = f (u) та — диференційовні функції від своїх аргументів, то похідна складної функції існує і дорівнює .
Таким чином, похідна складної функції дорівнює добутку похідної зовнішньої функції за проміжним аргументом на похідну проміжного аргументу за незалежною змінною.
Похідна неявної функції. Нехай рівняння F (x; y) = 0 визначає у як неявну функцію від х. Надалі будем вважати, що ця функція — диференційовна.
Продиференціювавши за х обидві частини рівняння F (x; y) = 0, дістанемо рівняння першого степеня відносно . З цього рівняння легко знайти , тобто похідну неявної функції.
11.
1) Похідна складеної функції Якщо функція має похідну в точці х, а функція – має похідну в точці , тоді складена функція диференційовна в точці х, причому
![]() або
або 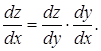
Наведене правило обчислення похідної складеної функції застосовується і для композиції довільного скінченого числа функцій.
Наприклад,
для складеної функції виду ![]() ,
де
,
де ![]() ,
, ![]() ,
, ![]() –
диференційовні у відповідних точках
функції, має місце рівність
–
диференційовні у відповідних точках
функції, має місце рівність
 .
.
Якщо неперервна та строго монотонна в деякому околі точки х функція має похідну в цій точці, тоді обернена функція в точці у має похідну, причому
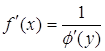 .
.
3) Логарифмічне диференціювання
Якщо маємо громіздкі вирази, що містять добутки, частки, степені, то перш, ніж знаходити похідну, вираз рекомендується прологарифмувати.
Приклад
1. Знайти
похідну функції 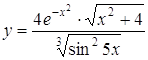 .
.
Розв’язання. Прологарифмуємо функцію:
![]()
Знайдемо похідну від лівої та правої частин:

звідки
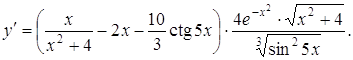
Такий же спосіб використається для знаходження похідної так званої степенево-показникової функції
![]() .
.
2) Якщо функція y f u = ( ) має похідну в точці u , а функція u g x = ( ) – в точці x ,
то складена функція y f g x = ( ( )) диференційована в точці x , причому
( ) ( )
' ' '
y f u g x
Іншими словами, похідна складеної функції y f u = ( ) , u g x = ( ) дорівнює добутку
похідної від зовнішньої функції, взятої по внутрішньому аргументу u , і похідної
від внутрішньої функції, взятої по незалежній змінній x . Якщо u x( )- диференційовна в точці x функція, то виконуються такі формули
диференціювання складених функцій :
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
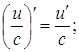 (4)
(4)
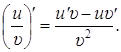 (5)
(5)
Похідні основних елементарних функцій
![]() (6)
(6)
![]() (7)
(7)
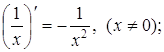 (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
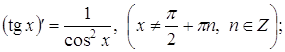 (12)
(12)
![]() (13)
(13)
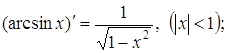 (14)
(14)
 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
 (18)
(18)
 (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
12. Похідні та диференціали вищих порядків
(higher derivative, higher-order differential)
Нехай
функція ![]() диференційовна
на проміжку X,
а
диференційовна
на проміжку X,
а ![]() її
похідна, яка також є функцією відносно x.
Від цієї функції знову можна шукати
похідну за умови, що вона існує на
заданому проміжку. Похідна від
похідної
називається похідною
другого порядку (second-order derivative)
функції
і
позначається одним із символів:
її
похідна, яка також є функцією відносно x.
Від цієї функції знову можна шукати
похідну за умови, що вона існує на
заданому проміжку. Похідна від
похідної
називається похідною
другого порядку (second-order derivative)
функції
і
позначається одним із символів:
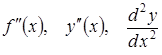 .
.
Так
у фізиці, якщо ![]() закон,
за яким змінюється пройдений шлях при
прямолінійному русі точки,
то
закон,
за яким змінюється пройдений шлях при
прямолінійному русі точки,
то ![]() є прискоренням (acceleration) цієї
точки в момент часу t.
є прискоренням (acceleration) цієї
точки в момент часу t.
Аналогічно  і
т. д.
і
т. д.
Взагалі похідною n-го
порядку від
функції
називається
похідна від похідної ![]() -го
порядку і позначається
-го
порядку і позначається
![]() ,
або
,
або ![]() ,
або
,
або ![]() .
.
Зауваження. При ![]() ,
похідну n-го
порядку позначають відповідно
,
похідну n-го
порядку позначають відповідно ![]() ;
при
;
при ![]() позначають:
позначають: ![]() або
або ![]() .
.
Приклад 3.17. Знайти похідну другого порядку від функції
![]() .
.
Розв’язання. Знаходимо
спочатку ![]() за
формулою
за
формулою ![]() .
.
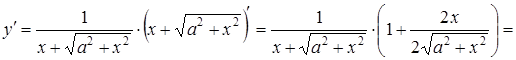
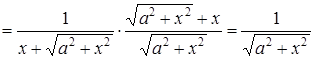 .
.
Знаходимо похідну від отриманої функції:
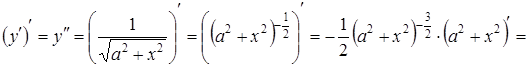
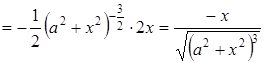 ,
тобто
,
тобто 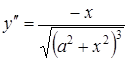 .
.
Приклад
3.18. Знайти
похідну n-го
порядку від функції ![]() .
.
Розв’язання.

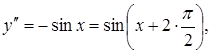
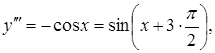
![]()
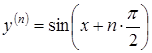 .
.
Формула
Лейбніца. Якщо
функції ![]() ,
, ![]() мають
похідні до n-го
порядку включно, то для обчислення
похідної n-го
порядку від добутку цих функцій
використовують формулу Лейбніца:
мають
похідні до n-го
порядку включно, то для обчислення
похідної n-го
порядку від добутку цих функцій
використовують формулу Лейбніца:
![]() .
(3.14)
.
(3.14)
Похідні
вищих порядків від функцій, заданих
параметрично. Якщо
функції ![]() і
і ![]() параметрично
задають функцію
параметрично
задають функцію ![]() ,
то похідні
,
то похідні 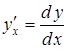 ,
, 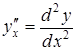 ,
можна послідовно обчислити за формулами:
,
можна послідовно обчислити за формулами:
 ,
, 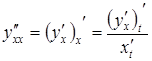 і
т. д.
і
т. д.
Так, для похідної другого порядку має місце формула:
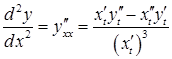 .
(3.15)
.
(3.15)
Приклад
3.19. Знайти
похідну ![]() функції
,
заданої параметрично:
функції
,
заданої параметрично: ![]() ,
, ![]() .
.
Розв’язання.
![]() .
.
за формулою (3.15)
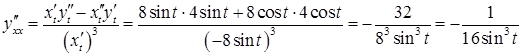 .
.
Диференціали вищих порядків. Нехай функція диференційовна на проміжку X. Її диференціал
![]()
називається
також диференціалом
першого порядку і
його можна розглядати як функцію
змінної x(приріст
аргументу ![]() вважається
сталим).
вважається
сталим).
Означення
3.4. Диференціалом другого
порядку (second differential) функції
в
точці xназивається
диференціал від її диференціала першого
порядку (за умови, що повторний приріст
незалежної змінної x збігається
з попереднім
)
і позначається ![]() :
:
![]() .
.
За означенням маємо
![]() ,
,
позначають ![]() .
Таким чином
.
Таким чином
![]() .
(3.16)
.
(3.16)
Аналогічно, диференціалом n-го
порядку (позначається ![]() ), n=2,3,...
називається диференціал від диференціала
порядку
за
умови, що в диференціалах весь час
беруться одні й ті самі прирости
незалежної
змінної x.
Тобто
), n=2,3,...
називається диференціал від диференціала
порядку
за
умови, що в диференціалах весь час
беруться одні й ті самі прирости
незалежної
змінної x.
Тобто
![]() .
.
При цьому справедлива формула:
![]() .
(3.17)
.
(3.17)
Приклад
3.20. Обчислити
,
якщо ![]() .
.
Розв’язання. Скористаємось
формулою (3.16). Для цього знайдемо ![]() :
:
![]() ,
, 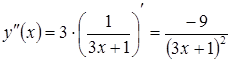 .
.
Отже

13.
1.) Позначимо
через D деякий
безліч точок в п-мірному просторі.
Якщо
задано закон f ,
В силу якого кожній точці М
(х ![]() ;...; Х
;...; Х ![]() )
) ![]() D ставиться
у відповідність число і, то
говорять, що на безлічі D визначена функція і = f
(х
;...; Х
).
Безліч
точок М (х
;...; Х
),
Для яких функція і = f
(х
;...; Х
)
Визначена, називають областю
визначенняцієї функції і
позначають D (f).
Функції багатьох
змінних можна позначати одним символом і = f
(М), вказуючи розмірність простору,
якому належить точка М.
Функції
двох змінних можна зобразити графічно
у вигляді деякої поверхні.
Графіком
функції двох змінних z = f (х;
у) у прямокутній системі
координат Оху називається геометричнемісце
точок у тривимірному просторі, координати
яких (х; у; z) задовольняють
рівнянню z = f (х;
у).
2.) Позначимо через
D ставиться
у відповідність число і, то
говорять, що на безлічі D визначена функція і = f
(х
;...; Х
).
Безліч
точок М (х
;...; Х
),
Для яких функція і = f
(х
;...; Х
)
Визначена, називають областю
визначенняцієї функції і
позначають D (f).
Функції багатьох
змінних можна позначати одним символом і = f
(М), вказуючи розмірність простору,
якому належить точка М.
Функції
двох змінних можна зобразити графічно
у вигляді деякої поверхні.
Графіком
функції двох змінних z = f (х;
у) у прямокутній системі
координат Оху називається геометричнемісце
точок у тривимірному просторі, координати
яких (х; у; z) задовольняють
рівнянню z = f (х;
у).
2.) Позначимо через ![]() (М;
М
(М;
М ![]() )
Відстань між точками М і М
. Якщо п =
2, М (х; у), М
(Х
; У
),
То
(М;
М
)
=
)
Відстань між точками М і М
. Якщо п =
2, М (х; у), М
(Х
; У
),
То
(М;
М
)
= ![]() .
У п-мірному просторі
(М;
М
)
=
.
У п-мірному просторі
(М;
М
)
= ![]() .
Нехай
на множині D задано функцію і = f
(М).
Число А називається границею
функції і = f (М) в
точці М
, Якщо
для довільного числа
.
Нехай
на множині D задано функцію і = f
(М).
Число А називається границею
функції і = f (М) в
точці М
, Якщо
для довільного числа ![]() >
0 знайдеться таке число
>
0 знайдеться таке число ![]() >
0, що для всіх точок М
D, які
задовольняють умові 0 <
>
0, що для всіх точок М
D, які
задовольняють умові 0 < ![]() (М;
М
)
<
(М;
М
)
< ![]() ,
Виконується нерівність
,
Виконується нерівність
![]()
![]() .
Властивості
границь функції однієї змінної
зберігаються і для функцій багатьох
змінних, тобто якщо функції f (М) і g
(М) мають в точці М
кінцеві межі,
то
1.
.
Властивості
границь функції однієї змінної
зберігаються і для функцій багатьох
змінних, тобто якщо функції f (М) і g
(М) мають в точці М
кінцеві межі,
то
1. ![]() = З
= З ![]() ,
2.
,
2. ![]() =
=
![]()
![]() ,
3.
,
3. ![]() =
.
4.
=
.
4. 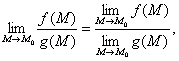 якщо
якщо
![]() .
Зауважимо,
що якщо межа
існує,
то він не повинен залежати від шляху,
по якому точка М прагне до
точки М
.
Функція і = f
(М) називається безперервної
в точці М
,
Якщо
= F
(М
).
Функція і = f
(М) називається безперервної
на безлічі D, якщо вона
неперервна в кожній точці М
D.
Точки, в яких безперервність
функції порушується, називаються точками
розриву функція. Точки розриву
можуть бути ізольованими, створювати
лінії розриву, поверхні розриву і т. д.
.
Зауважимо,
що якщо межа
існує,
то він не повинен залежати від шляху,
по якому точка М прагне до
точки М
.
Функція і = f
(М) називається безперервної
в точці М
,
Якщо
= F
(М
).
Функція і = f
(М) називається безперервної
на безлічі D, якщо вона
неперервна в кожній точці М
D.
Точки, в яких безперервність
функції порушується, називаються точками
розриву функція. Точки розриву
можуть бути ізольованими, створювати
лінії розриву, поверхні розриву і т. д.
3) 1 Частинні похідні
Нехай функція визначена в деякому околі точки . Надамо змінній x приросту, залишаючи змінну незмінною, так, щоб точка належала заданому околу.
Величина
називається частинним приростом функції за змінною x.
Аналогічно вводиться частинний приріст функції за змінною:
.
Якщо існує границя
,
то вона називається частинною похідною функції в точці за змінною x і позначається одним із таких символів:
.
Аналогічно частинна похідна функції за визначається як границя
і позначається одним із символів:
.
Згідно з означенням при знаходженні частинної похідної обчислюють звичайну похідну функції однієї змінної x, вважаючи змінну сталою, а при знаходженні похідної сталою вважається змінна x. Тому частинні похідні знаходять за формулами і правилами обчислення похідних функцій однієї змінної.
Частинна похідна (або) характеризує швидкість зміни функції в напрямі осі (або).
З'ясуємо геометричний зміст частинних похідних функції двох змінних. Графіком функції є деяка поверхня (рис 1). Графіком функції є лінія перетину цієї поверхні з площиною. Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо, що, де- кут між віссю і дотичною, проведеною до кривої в точці. Аналогічно.
Рисунок 1 - Геометричний зміст частинних похідних
Для функції n змінних можна знайти n частинних похідних:
,
де
,
.
Щоб знайти частинну похідну, необхідно взяти звичайну похідну функції за змінною, вважаючи решту змінних сталими.
Якщо функція задана в області і має частинні похідні в усіх точках, то ці похідні можна розглядати як нові функції, задані в області.
Якщо існує частинна похідна за x від функції, то її називають частинною похідною другого порядку від функції за змінною x і позначають або .
Таким чином, за означенням
або.
Якщо існує частинна похідна від функції за змінною, то цю похідну називають мішаною частинною похідною другого порядку від функції і позначають, або.
Отже, за означенням
або .
Для функції двох змінних можна розглядати чотири похідні другого порядку:
.
Якщо існують частинні похідні від частинних похідних другого порядку, то їх називають частинними похідними третього порядку функції, їх вісім:
.
Виникає запитання: чи залежить результат диференціювання від порядку диференціювання? Інакше кажучи, чи будуть рівними між собою мішані похідні, якщо вони взяті за одними і тими самими змінними, одне й те саме число разів, але в різному порядку? Наприклад, чи дорівнюють одна одній похідні
і або і?
У загальному випадку відповідь на це запитання негативна.
Проте справедлива теорема, яку вперше довів К.Г.Шварц.
Теорема (про мішані похідні). Якщо функція визначена разом із своїми похідними в деякому околі точки , причому похідні та неперервні в точці, то в цій точці
.
Аналогічна теорема справедлива для будь-яких неперервних мішаних похідних, які відрізняються між собою лише порядком диференціювання.
