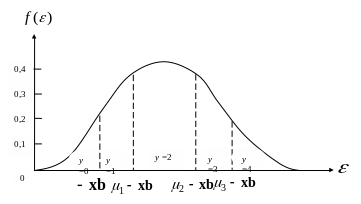Тест правдоподобия 1-го типа
Используя построенную модель, рассчитаем вероятности успеха в случае выбора инвестиционного проекта, связанного с рестораном, кафе и бистро, при условии:
1)
;
;
;
;
;
;
2)
;
;
;
;
;
.
В первом случае наиболее вероятен успех при выборе проекта, связанного с бистро, а во втором – ресторана.
Предельный эффект
имеет смысл рассчитывать только для
фактора
:
для первого случая:
;
;
;
;
2) для второго случая:
;
;
;
.
Анализ предельных эффектов показывает, что в первом случае рост числа обслуживаемых одновременно клиентов увеличивает вероятность выбора среди рассматриваемых вариантов в первую очередь кафе, а затем ресторана. Во втором случае увеличивается вероятность выбора только ресторана. Причем, увеличение вероятностей выбора одних вариантов происходит за счет уменьшения вероятности выбора других.
Для остальных факторов в силу их дискретного характера следует рассчитывать непосредственно вероятности. Например,
для
при
;
;
;
;
;
для при при ; ;
;
;
.
Получаемые распределения сравниваются с исходным распределением и делаются соответствующие выводы. В случае предпочтительность выбора не изменилась, а в случае предпочтительнее выбрать кафе.
3.5.3. Пробит- и логит- модели множественного выбора в ранговых шкалах. Среди задач решаемых экспертами наиболее популярна задача ранжирования. Прямые методы решения этой задачи со всеми деталями были рассмотрены во второй главе. Здесь, продолжая развивать идею построения моделей по данным, представляющим результаты экспертного опроса, мы рассмотрим схему построения пробит и логит-моделей множественного выбора для случая, когда моделируемая переменная измеряется в ранговой шкале.
Приведем описание нескольких ситуаций, формализация которых приводит к задачам подобного рода:
Определение рейтинга облигаций по независимому опросу экспертов.
Определение рейтинга банков по их надежности.
Моделирование результатов дегустационных тестов.
Определение приоритетов по результатам обследования общественного мнения.
Выяснение приоритетности социальных программ по результатам голосования.
Для моделирования
подобных ситуаций будем считать, что
есть переменная
,
значения которой определяются некоторым
набором объясняющих переменных в
соответствии с зависимостью
.
(3.111)
Сама переменная не наблюдаемая величина, но известны значения дискретной переменной, которые в нашем представлении связаны с ненаблюдаемой следующими соотношениями
. . . . . . . . (3.112)
Неравенства
реализуют некую форму цензурирования.
Причем уровни цензурирования
неизвестны и представляют собой
параметры, оцениваемые вместе с
коэффициентами
.
Заменим в неравенствах
ненаблюдаемую переменную ее модельным
представлением и вычтем
из каждой части
. . . . . . . . (3.113)
Будем считать, что
случайная величина
нормально распределена по наблюдениям
и, кроме того, нормирована таким образом,
что имеет нулевое математическое
ожидание и единичную дисперсию. В случае
построения логит-модели предполагается,
что случайная велична
имеет логистическое распределение.
Для пробит-модели выписанные неравенства позволяют записать следующие вероятности
. . . . . . . . . . . (3.114)
Чтобы все вероятности были положительными, оцениваемые параметры положения должны удовлетворять неравенствам
.
(3.115)
Смысл параметров положения хорошо иллюстрирует рис. 3.1
