4.2.6. Декомпозиции, сохраняющие зависимости.

Как уже отмечалось, желательно, чтобы декомпозиция обладала свойством соединения без потерь. Это является гарантией того, что любое отношение, являющееся текущим значением схемы, может быть восстановлено из его проекций на подсхемы декомпозиции. Другое важное свойство декомпозиции =(R1, R2, ..., Rk) схемы отношения R заключается в том, чтобы множество зависимостей F, заданных для R, было выводимым из проекций F на подсхемы Ri.

Формально проекцией F на множество атрибутов Z, обозначаемой _Z(F), называется множество зависимостей X—>Y в F⁺, таких, что X,YZ.

Часто удобнее вместо _Z(F) рассматривать его минимальное покрытие. Например, если имеется R=({Al, А2, А3, А4}, {Al—>A2; А2—>АЗ; A3—>A4}), Z={А1, АЗ, А4}, то _Z(F)={А1>A3; A3>A4}. Здесь записано минимальное покрытие проекции F.

Декомпозиция  сохраняет множество зависимостей F, если из объединения всех зависимостей, принадлежащих _Ri(F), i=1, 2, …, k, логически следуют все зависимости F.

Стремление к тому, чтобы  сохраняла F, естественно. Зависимости в F могут рассматриваться как ограничения целостности для схемы R. Если из спроецированных зависимостей не следует F, то возможны такие текущие значения Ri, представляющие отношение R в декомпозиции , которые не удовлетворяют F, даже тогда, когда  обладает свойством соединения без потерь относительно F. Для избежания подобных аномалий требуется в случае обновления базы данных осуществлять операцию естественного соединения, чтобы проверять, не нарушаются ли зависимости из F.

Следует отметить, что декомпозиция может обладать свойством соединения без потерь, но не сохранять F, например:

Для схемы R=({А1, А2, АЗ}, {А1,А2>A3; АЗ>А1}) получена декомпозиция =(R1, R2), где R1=({А1, А2}), R2=({А2, АЗ}).

Декомпозиция =(R1, R2) обладает свойством соединения без потерь, это следует из того, что {Al, A2}{А2, A3}={A2} и A2—>A3=U2\U1. В то же время зависимость А1,А2—>АЗ не выводится из проекций F на множества U1 и U2.

Возможен и обратный случай, когда декомпозиция сохраняет зависимости, но не обладает свойством соединения без потерь. Например, это имеет место для следующей схемы R и ее декомпозиции:

R=({Al, А2, А3, А4}, {Al—>A2; A3—>А4}),  =({А1, А2}, {АЗ, А4}).

В теории проектирования реляционных баз данных разработаны несколько нормальных форм схем отношений, в различной степени устраняющие перечисленные ранее возможные недостатки исходных схем.

4.3 Нормальные формы отношений.

4.3.1. Первая и вторая нормальные формы схем отношений.

Говорят, что отношение нормализовано или находится в первой нормальной форме, если домен каждого атрибута состоит из неделимых значений, а не множеств или кортежей из элементарного домена или доменов, то есть значения атрибутов – это некоторые элементарные величины, не имеющие структуры. В дальнейшем будем рассматривать только нормализованные отношения.

Понятие второй нормальной формы тесно связано с понятием полной функциональной зависимости.

Вторая нормальная форма схемы отношения это либо данная схема, если она нормализована и содержит только полные функциональные зависимости непервичных атрибутов от ключей, либо декомпозиция схемы, каждая из подсхем которой обладает указанными свойствами, а сама декомпозиция имеет свойство соединения без потерь.

Заметим, что если в схеме отношения все атрибуты первичные или же любой ключ состоит только из одного атрибута, то схема заведомо находится во второй нормальной форме.

Вторая нормальная форма существует для любой схемы отношения, это следует из следующего простого утверждения.

Теорема Хита. Пусть задана схема отношения R=(U, F) и U=XYZ, X—>Y, тогда декомпозиция R=(R1, R2), где R1 = (XY), R2=(XZ), обладает свойством соединения без потерь.

Это утверждение дает очевидный способ приведения схемы отношения с неполной функциональной зависимостью набора непервичных атрибутов В от ключа К ко второй нормальной форме.

Пусть U – набор всех атрибутов отношения R. Присутствие в отношении неполной зависимости В от ключа К означает, что  A ((AK)  (BA)  (A>B)). Построим декомпозицию Rl=(AB), R2=(U\B). Отношения R1 и R2 уже не содержат указанной неполной зависимости, и полученная декомпозиция обладает свойством соединения без потерь. Далее, аналогичные проверки применяются к отношениям R1 и R2, так продолжается до тех пор, пока не получим декомпозицию =(R1, R2, ..., Rk), каждая из подсхем которой не содержит неполных зависимостей непервичных атрибутов от ключей. Декомпозиция  и является искомой второй нормальной формой схемы R.

Описанный способ обосновывается также следующими свойствами декомпозиции.

а) Пусть задана схема отношения R=(U, F), =(R1, R2, ..., Rk) –декомпозиция R, обладающая свойством соединения без потерь относительно F, a Fi для каждого i означает проекцию U на Ri. Допустим, что =(S1, S2, ..., Sm) – декомпозиция Ri, обладающая свойством соединения без потерь относительно Fi. Тогда декомпозиция R в подсхемы (R1, ..., Ri-l, S1, ..., Sm, Ri+l, ..., Rk) – также обладает свойством соединения без потерь относительно F.

б) Предположим R, F,  тe же, что в пункте а). Пусть =(R1, R2, ..., Rk, Rk+l, ..., Rt) – декомпозиция R в некоторое множество схем, которое включает все схемы из . Тогда  также обладает свойством соединения без потерь относительно F.

Таким образом, если декомпозиция обладает свойством соединения без потерь, то “разбив” некоторую схему декомпозиции на еще более мелкие подсхемы, обладающие свойством соединения без потерь относительно разбиваемой подсхемы, опять получим декомпозицию исходной схемы, обладающую этим свойством. Добавление к декомпозиции любого количества подсхем не нарушает свойства соединения без потерь. Эти свойства часто используются также для приведения отношений к третьей и усиленной третьей (рассмотрены ниже) нормальным формам.

Подробнее остановимся также на задаче проектирования набора функций F на схемы декомпозиции. В общем случае это задача довольно трудоемкая, но при приведении отношений к нормальным формам чаще всего в отдельные подсхемы выделяются некоторые зависимости из F. Например можно поступать следующим образом:

Пусть задана схема R=(U, F), считаем, что все зависимости в F в правой части содержат только один атрибут (всегда можно преобразовать F к такому виду). Допустим, строится декомпозиция R1=(U1) и R2=(U2), причем Ul=X{y}, ХU, уU, (Х>у)F⁺; U2=U\{y}.

Для получения проекции F на U2 достаточно найти все зависимости вида Xi—>у, содержащиеся в F. Затем каждую зависимость, содержащую атрибут у в левой части заменить группой зависимостей, подставляя вместо у множество Xi. Те зависимости, где атрибут у находится в правой части, удаляются, в результате получим проекцию F на U2 (точнее покрытие проекции). Для получения проекции F на U1 придется просмотреть замыкания подмножеств множества U1 относительно F, но множество U1 обычно невелико.

Заметим также, что всегда удобнее работать, если все зависимости F полные (такое преобразование F сделать не сложно), модифицированные зависимости при получении проекции F на U2 также имеет смысл приводить к полным. При рассмотрении U1 в случае, если Х>у – полная зависимость, следует просматривать только замыкания подмножеств, содержащих y.

Декомпозицию схемы отношения при переходе ко второй нормальной форме удобно строить в виде дерева. Пусть задана схема R=(U, F). Вначале дерево состоит только из одной вершины, соответствующей отношению R. Далее находим зависимость непервичного атрибута y от части ключа Х, (Х—>у)F, и строим две нижестоящие вершины, одна из них соответствует отношению R1=(U\{y}), вторая отношению R2=(X{y}), далее, если необходимо, аналогичную декомпозицию осуществляем для висящих вершин (листьев) дерева, этот процесс продолжается до тех пор, пока все висящие вершины не будут соответствовать подсхемам во второй нормальной форме, совокупность этих подсхем и является искомой декомпозицией исходной схемы отношения.

В принципе можно рассматривать вместо одного атрибута у в правых частях выделяемых зависимостей множества атрибутов, но тогда несколько усложнится задача проектирования F на подсхемы.

Желательно также рассматривать только полные функциональные зависимости.

Пример.

Для схемы R=(U, F), U={A1, A2, А3, А4, А5, А6, А7},

F={А1—>A3; АЗ—>А5; А2—>А4; А4—>А6; А5,А6>А7}) требуется получить вторую нормальную форму схемы отношения R. Отношение имеет единственный ключ К={А1, А2}, множество непервичных атрибутов {АЗ, А4, А5, А6, А7}.

Зависимость А1—>A3 является нежелательной, так как непервичный атрибут A3 зависит от части ключа. Выделяем эту зависимость в отдельное отношение, получаем:

R1=({A1, A2, A4, A5, A6, A7},

{Al>A5; А2—>А4; А4>А6; А5,А6>А7}).

Зависимость А1—>A5 получена в результате проецирования F нa подсхему R1; ключом отношения R1 является {А1, А2}.

R2=({A1, A3}, {A1>A3}), единственный ключ R2 – {А1}.

R2 находится во второй нормальной форме, в R1 нежелательной является зависимость А1—>А5. Получаем декомпозицию R1:

R11=({A1, A2, A4, A6, A7}, {A2>А4; А4>А6; А1,А6>А7}), ключ R11 – {А1, А2},

R12=({A1, A5}, {A1>A5}), ключ R12 – {А1}.

R12 находится во второй нормальной форме, в R11 нежелательной является зависимость А2>А4, получаем декомпозицию R11:

R111=({А1, А2, А6, А7}, {А2>A6; А1,А6—>А7}), ключ – {А1, А2},

R112=({A2, A4}, {A2>А4}), ключ R112 – {А2}.

R112 находится во второй нормальной форме, в R111 нежелательной является зависимость А2—>А6, получаем декомпозицию R111:

R1111=({A1, A2, A7}, {А1,А2—>А7}), ключ R1111 – {А1, А2},

R1112=({A2, A6}, {A2> A6}) , ключ R1112 – {А2}.

R1111 и R1112 находятся во второй нормальной форме, искомая декомпозиция (вторая нормальная форма отношения R) имеет вид

=(R2, R12, R112, R1111, R1112).

Дерево декомпозиции имеет вид:

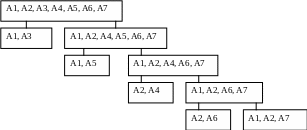
Схема отношения может иметь более одной второй нормальной формы, так, в приведенном примере второй нормальной формой исходной схемы является также декомпозиция

₁=({A1, A3}, {АЗ, А5}, {А2, А4}, {А4, А6}, {А5, А6, А7}),

причем  удачнее, чем ₁, в смысле минимизации аномалий базы данных.

В приведенном примере ситуация упрощалась тем, что отношение имеет единственный ключ (рассматривать надо неполные зависимости непервичных атрибутов от всех ключей).