25. Спектр щелочных металлов.

(на внешней орбите 1е, Li, Na, Ka, Ru и т.д.)

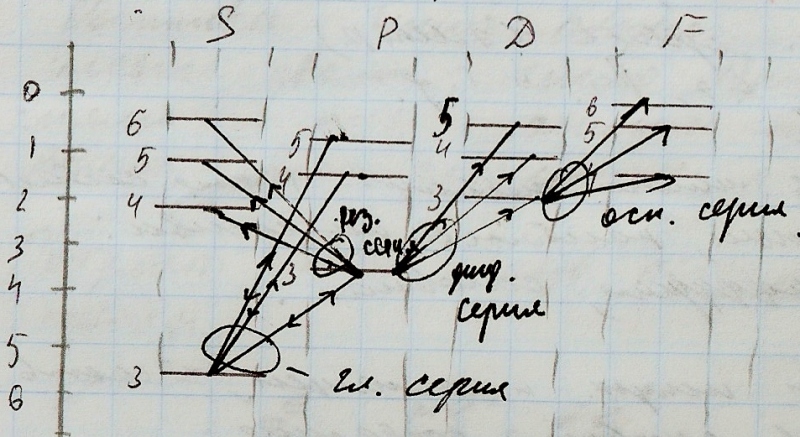
Спектроиспускание атомов щелочных металлов также состоят из нескольких серий, наиболее интенсивн.: главная, резкая, диффузная, основная.

Главная-набл. При испускании и поглащен.=>соотв. Переходом атома в основное состояние.

Резкая, диф.-состоит из резких спектральн. Линий и диф./размытых спектр. Линий.

Основная серия-сходство с сериями атома водорода. Выражение частот, справедл. Для любых серий: R-const Ридберга, n-целые числа, альфа-дробные.

Пример. Атом Na –в спектре присутств. Все 4 серии.

1)Резкая 2)Главная: 3)Диффузная 4)Основная . В атомной физике принято записыв. Переменные термы, (S,P,D,F). Соотв. Расчеты показыв., что постоян. Термы равны: , , , :

26. Водородоподобные системы.

Потенциальная энергия

Стационарное уравнение Шредингера:

Ввиду того, что поле системы центральносимметричное, это уравнение решается в сферической системе координат.

Напоминание.

Опуская решение, получаем: требуемые решения для пси-функции лишь в двух случаях.

1. 2.

Квантовые числа:

Рассмотрим атом водорода:

_____________________________________

Запишем уравнение Шредингера:

С-константа, A0-коэффициент с размерностью длины.

Подставляя в уравнение и сократив, получаем:

Без доказательства напишем:

Таким образом, получаем:

27. Тонкая структура спектров. Спин электрона.

Спектрометры с высокой разрешающей способностью показали: для натрия линии спектра в большинстве своем не одиночные, а двойные. Причем расщепление линий обусловлено расщеплением энергетических уровней.

Структура спектра, отражающая расщепление линий на компоненты – тонкая структура спектра. Линии спектра (из нескольких компонентов) – мультиплеты.

Число компонентов в мультиплете различно: (1-синглета, 2-дублет, 3-триплет, 4-квартет, 5-квинтет).

Гаудсмит и Уленбек в 1930-х годах выдвинули гипотезу о наличии у электрона собственного момента количества движения -

Он никак не связан с движением электронов в пространстве. В науке собственный момент количества движения – спин.

Величина спина определяется по законам квантовой механики спиновым числом S. Величина для электрона -

В этом случае

Собственный момент – векторная величина.

магнитное спиновое число.

Собственный магнитный момент

Знак «минус» показывает, что и направлены в разные стороны.

Исследование оптических спектров щелочных металлов (в частности натрия) показывает, что момент импульса атомного остатка (ядро и все электроны, кроме внешного-оптического) равен нулю. Это означает, что момент импульса атома щелочного металла равен моменту импульса его оптического электрона.

Очевидно, что момент импульса электрона равен сумме орбитального и спинового моментов.

Орбитальный момент обусловлен движением атома по орбите). Спиновый момент не связан с орбитальным движением.

Суммарный момент импульса

j-квантовое число суммарного момента.

У натрия в основном состоянии

Вывод. Каждая из термов (кроме S) распадается на 2 ряда.Структура становится дуплетной.

Пример: