1) 27 : 3 – Было тетрадей у Миши.

2) (27 : 3) + 3 – было тетрадей у Лёни.

3) (27: 3) – 3 – Было тетрадей у Алеся.

5. Решение задачи по действиям с частичными пояснениями результатов:

1. 3 + 3 + 3 = 9 (т.).

2. 27 + 9 = 36 (т.).

3. 36 : 3 = 12 (т.) – было тетрадей у Лени.

4. 12 – 3 = 9 (т.) – было тетрадей у Миши.

5. 9 – 3 = 6 (т.) - было тетрадей у Алеся.

6. Алгебраический способ решения задачи

Используя чертёж задачи, составим уравнение:

Х – количество тетрадей у Алеся,

Х + 3 – количество тетрадей у Миши,

(Х + 3) + 3 – количество тетрадей у Лёни.

Уравнение: Х + (Х + 3) + (Х + 3) + 3 = 27.

Используя переместительное и сочетательное свойства сложения,запишем уравнение:

( Х + Х + Х) + (3 + 3 + 3 ) = 27.

Заменив сложение умножением, запишем уравнение:

Х  3 + 3  3 = 27.

Решаем уравнение: Х  3 + 9 = 27.

Х  3 = 27 – 9

Х  3 = 18

Х = 18: 3

Х = 6

Проверка: 6 + (6 + 3) + (6 + 3) + 3 =27

27 = 27

Ответ: было тетрадей : у Алеся – 6, у Миши – 9, у Лёни – 12.

Проверка решения: 6 + 9 + 12 = 27 (т.).

8. Геометрический способ решения задачи Используя чертёж, найдём сумму отрезков:

А. 1) (27-9):3=6 (т.) у Алеся

М. 3 т. 27 т. 2) 6+3=9 (т.) у Миши

Л. 3 т. 3) 9+3=12 (т.) у Л ёни

У Алеся У Миши У Лёни

Перенесём три длинных и три коротких отрезка в один отрезок:

3т.3т.3т.

27 т. 1) 33 = 9 (т.)

Как известно, один маленький отрезок моделирует 3 тетради, а 3 таких же отрезка 3  3 = 9 (т.), три больших отрезка моделируют 27 – 9 = 18 (т.). Один большой отрезок моделирует 18 : 3 = 6 (т.) – количество тетрадей у Алеся. У Миши тетрадей 6 + 3 = 9 (т.), а у Лёни 9 + 3 = 12 (т.).

9.Способы дополнительной работы над задачей

.9.1. Выбор рационального способа решения

После анализа всех возможных способов решения задачи ученику обычно предлагается выбрать наиболее рациональный.

.9.2. Объяснение выражений, составленных по условию задачи

Так, у решающих обычно возникают трудности в пояснении выражений 3 + 3 + 3; 27 – 9; 27 + 9.

.9.3. Выбор модели к задаче

Обычно выбор модели зависит от вида и способа решения задачи. Модель должна полностью представлять все числовые данные, отно-шения и зависимости задачи, подчёркивая наиболее существенные из них, их структуру.

9.4. Изменение текста задачи, чтобы исследовать, к какому решению это приведёт. Так, вначале мы значительно изменили текст задачи, сделали его удобным к пониманию как по форме, так и по содержанию. Двухкратная замена отношений на 3 больше отноше-ниями на 2, 4, 5, 6 больше приведёт к другим ответам задачи.

МОДЕЛЬ ПОСТАНОВКИ И РЕШЕНИЯ УЧЕБНОЙ ЗАДА

Основным недостатком методики постановки и решения задач является неразработанность способов управления их составлением и решением путём самостоятельной поис ковой деятельности учащихся (приёмов, методов и планов ПДУ). Создание таких способов вытекает из нашей модели, учитывающей узловые элементы теории функциональных систем академика П.К. Анохина.

1. (2) (3) (4) (5) (6) (7) (8)

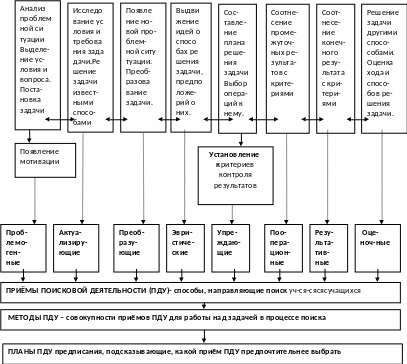
(1) (2) (3) (4) (5) (6) (7) (8)

От хорошего функционирования мозга во многом зависит успех в деятельности человека, а у обучаемогоего учебно-поисковой деятельности. Она-то как раз и осуществляется им при поиске ре-шения учебных задач, системы которых должны быть созданы в каждом учебном предмете. Была разработана модель учебной задачи на основе теории функциональных систем академика П.К. Анохина. Модель предложена для ксерокопирования. Предлагаем описание 8 моментов постановки и решения задачи.

К каждому моменту разработаны некоторые приёмы поисковой деятельности учащихся (ПДУ). Они носят эвристический характер и призваны облегчить прохождение каждого из 8 моментов работы мозга в нашей модели. Появление недо-рогих ЭВМ с большим объёмом оперативной памя-ти, а также средств для оперативного выявления затруднений при поиске решения задач позволяет этот процесс сделать самоуправляемым. 1-ый момент. Постановка любой задачи начинается с выделение её структурных элементов путём анализа проблемной ситуации, вычленения области поиска, установления известных и неизвестных данных задачи и формулировки её требования. Для преодоления затруднений в прохождении данного момента разработаны проблемогенные приёмы ПДУ, облегчающие анализ проблемной ситуации с целью выделения условия и вопроса и формулировки проблемы в виде задачи.

2-ой момент. Решающий обычно пытается исследовать условие и вопрос задачи. Ученик, как показывают наблюдения, всегда ищет ответ задачи на основе известных способов решения, привлекает известные математические знания и собственный опыт. С целью улучшения эффективности такой работы разработаны актуализирующие приёмы ПДУ ( припоминание теоретических знаний и др.)

3-ий момент. В связи с тем, что ученик решает задачу проблемного характера на основе известных знаний и прошлого опыта, которых ему недостаточно, часто возникает новая проблемная ситуация. Тогда решающий перекодирует задачу (записывает её в других знаках, символах), переформулирует задачу (изменяет её словесное оформление), чтобы свести её к известной, аналогичной задаче, которую он уже решал. При этом ученик привносит новые математические сведения, изменяя форму представления данных и требований задачи. Чтобы поиск был результа-тивным, используются преобразующие приёмы ПДУ (краткая запись задачи, её моделирование в вид рисунка,чертежа,таблицы,схемы).

4-ый момент. В результате предыдущей поисковой работы у учащихся может возникнуть предположение о способе решения задачи. Они обычно пытаются обосновать его, представить в виде гипотезы. Для облегчения этой работы служат эвристические приёмы ПДУ: решение простых задач, входящих в составную; решение части задачи; решение аналогичной сюжетной задачи; припоми-нание нужного правила и др.

5-ый момент. Возникшее и обоснованное предположение, в свою очередь, приводит к определённым действиям, осуществляемым в определённой последовательности, т.е. к плану решения задачи. К каждому пункту плана подбираются соответствующие операции. В это же время актуализируются из памяти приблизительные параметры будущих результатов, критерии их контроля и оценки Для предупреждения возможных ошибок служат упреждающие приёмы ПДУ: прикидка результата и др.

6-ой момент. Выполняя операции, связанные с каждым пунктом плана, решающий соотносит их с прогнозируемыми параметрами и критериями. Если получение промежуточных результатов им соответствует, то деятельность решающего продолжается, в противном случае, прекращается. Тогда решающий обычно пытается вернуться на предыдущие этапы. Для повышения результативности такой работы на промежуточных этапах поиска решения и самого решения служат пооперационные приёмы ПДУ: установление границ операций и др.

7-ой момент. Конечный результат поисковой деятельности оформляется в виде ответа, который соотносится с выделяемыми критериями. К ним относятся известные способы проверки решения математических задач. В нашей модели они носят название результативных приёмов ПДУ. С помощью их оценивается весь процесс поиска решения задачи, констатируется возможность использования найденного способа для решения других задач.

8-ой момент. Оценочные приёмы ПДУ помогают выбрать лучший из разных способов решения задач, который отличается краткостью, доступностью и простотой вычислений. Кроме того, эти приёмы приучают мысленно воспроизвести весь процесс поиска, ощутимые в нём трудности и подумать, как использовать их при поиске решения других задач (рефлексия). Рассмотренные приёмы ПДУ изучаются и применяются сначала разрозненно, а затем объединяются вместе при постановке и решении задач определённого класса, обра-зуя своего рода совокупности приёмов ПДУ – методы поисковой деятельности учащихся. Для облегчения их актуализации и выбора приёма, адекватного классу задачи решаемой задачи, составлялются планы поисковой деятельности учащихся, обобщённость которых постепенно нарастает. Эти планы сначала даются в печатной, материа-лизованной форме, затем проговариваются решающими вслух, позже про себя. Постепенно в процессе формиро-вания у школьников учебно-поисковой деятельности приёмы , методы и планы ПДУ, эвристики, обоб-щаясь постепенно переходят во внутренний план. Обучение им и с помощью их целесообразно осуществлять по теории по-этапного формирования умственных действий.

2. СОСТАВЛЕНИЕ КАРТОЧЕК ДЛЯ САМОСТОЯТЕЛЬНОГО ПОИСКА РЕШЕНИЯ ЗАДАЧИ

Приведём пример карточки с задачей на поиск способа её решения. Решите задачу по плану.

…. Выберите нужное, вставьте пропущенные числа и буквы в карточке по задаче: С трёх участков собрали 2 т 156 кг картофеля: с первого – 1000 кг, со второго – в 2 раза меньше. Сколько килограммов картофеля собрали с третьего участка?

1. Прочитайте задачу 1-ый уч. ---- кг

сделайте её краткую 2-ой уч.в -- раза меньше 2 156 кг

запись 3-ий уч. ? кг

2.Составьте выражение 1) 2 156 – 1 000 : 2

и проверьте его по 2) 2 156 : 2 – 1 000

перфокарте 3) 2 156 – (1 000 :2 + 1 000)

4) 2 156 – 1 000 – 1 000 : 2

5) 2 156 – 1 000 : 2 – 1 000

3. Запишите решение задачи …………………………………

4. Запишите ответ…………………………………………………………

5.Проверьте: ----- + -- (кг) картофеля собрали с 1 и 2 участков,

решение в ---- раза масса картофеля со 2 участка меньше

массы картофеля с 1 участка.

6. Исследуйте задачу. Как будет изменяться масса картофеля, собранного с третьего участка, если масса картофеля, собранного со 2-го участка, будет меньше массы картофеля, собранного с первого участка, в 4 раза? в 5 раз?

7. Ответ проверьте по перфокарте:

1. увеличится в несколько раз;

2. увеличится на несколько единиц;

3. уменьшится в несколько раз;

4. уменьшится на несколько единиц

Перфокарта

Задания	Ответы
1	П 1	П 2
2	П 1	Прав.
3	Прав.	П 2
4	Прав.	П 2

П1.Решите похожую задачу: С трёх участков собрали 2 000 кг

картофеля: с первого – 1 000 кг, а со второго – 500 кг. Сколько килограммов картофеля собрали с третьего участка?

П 2. Сделайте к этой задаче чертёж:

1 уч. |------------| ….кг

2 уч. |-----| в ---- раза меньше … кг ___кг

3. уч. |--------|….кг.

Перфокарта заклеивается плотной бумагой с наколками, сделанными на швейной машине, как на почто-вых марках по форме клеточек. Клеточка открывается шари-ковой ручкой. Если ответ правильный, то в клетке стоит «Прав.». Если ответ неправильный, указывается помощник (П1,П2), записанный справа. В дальнейшем перфокарты в обучении поиску решения задач можно заменить персо-наль-ным компьютером с программой, содержащей банк посте-пенно усложняющихся задач и индивидуальной мерой помо-щи, исходя из уровня подготовки к поиску каждого решаю-щего (зоны его ближайшего развития), в виде подсказок, приёмов, методов и планов ПДУ.

В текст карточек для самостоятельной работы полезно включать планы по использованию: методов и приёмов ПДУ; эвристических подсказок (по оформлению решения, его проверке, по выбору рационального способа решения оценке решения, по дополнительной работе над задачей) Для осуществления мониторинга за процессом составле-ния задачи и поиска решения, проверки и оценки решения создаются тесты (входные, формирующие, диагностические, итоговые).

Применение указанных рекомендаций позволяет осуществлять эффективный поиск способа решения задач даже учащихся со слабой теоретической подготовкой и невысоким уровнем развития поисковой деятельности. Ещё более значительно можно повысить продуктивность самостоятельного поиска решения задач приме-нение заложенных в память ПЭВМ батарей задач с нарастающей трудностью решения с приёмами, методами, планами ПДУ, эвристическими подсказками, предложенными с учётом выявлено тестированием зоны ближайшего раз-вития обучаемого.