72. Вычисление длины дуги в декартовых координатах.

f(x)-непрерывная функция.

Разобьем отрезок [a,b] на n частей точками

a=x₀<x₁<…<x_i-1<x_i<…<x_n=b A=A₀, A₁, …, A_i-1, A_i, …, A_n=И

соединим эти точки отрезками прямых. В результате

получим ломанную линию, вписанную в данную дугу.

L_n = - длина ломанной.

Если для любых разбиений отрезка [a,b] существует предел , где λ=max{Δx₁, Δx₂, …, Δx_n}. Если этот предел существует и равен конечному числу, то его назыв. длиной дуги AB, а саам дуга при этом назыв. спрямляемой.

L _AB = .

Вычислим длину одного звена ломанной по теореме Пифагора.

|A_i-1A_i| = = = .

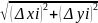(Δy_i = y_i-y_i-1 = y(x_i)-y(x_i-1) = y’(Ѯ_i) Δx_i по ф-ле Лагранжа ƎѮ_iϵ[x_i-1x_i]).

Тогда L_n= =

L_AB = = =

L_AB = .

73. Вычисление длины дуги в параметрическом виде.

AB: x=x(t), y=y(t) (α≤t≤β)

L_AB = = | замена x=x(t), y=y(t), y’(x)= | = = = = =

L_AB = .

74. Вычисление длины дуги в полярных координатах.

AB: r=r(ϕ), α≤ϕ≤β

Связь между декартовыми и полярными координатами: x=r*cosϕ, y=r*sinϕ. Тогда ур-е кривой AB можно задать в следующем виде: x=r(ϕ)cos ϕ=x(ϕ), y=r(ϕ)sin ϕ=y(ϕ).

L_AB = .

x'²(ϕ) = (r’(ϕ)cos ϕ – r(ϕ)sin ϕ)² = x’²cos² ϕ – 2r*r’sin ϕ*cos ϕ + r²sin² ϕ

y’²(ϕ) = (r’(ϕ)sin ϕ + r(ϕ)cos ϕ)² = r’²sin² ϕ + 2r*r’sin ϕ*cos ϕ + r²cos² ϕ

складывая, получаем: x’²(ϕ) + y’²(ϕ) = r’²(cos² ϕ + sin² ϕ) + r²(sin² ϕ + cos² ϕ) = r’² + r².

Тогда длина дуги L_AB = = .

L_AB = .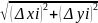