14. Энергия заряженного конденсатора

Если к обкладкам заряженного конденсатора присоединить проводники, замкнутые на электрическую лампочку, то лампочка вспыхнет. При этой вспышке в ней выделяется энергия, которая ранее была запасена в конденсаторе. Оценим величину этой энергии. Для этого начнем переносить с одной обкладки конден­са­тора маленькими порциями электрические заряды, заряжая конденсатор. К момен­ту очередного переноса заряда dq с одной обкладки на другую в конденсаторе соз­да­лась разность потенциалов . Тогда работа dA, затраченная на такой перенос, может быть записана, как

Работа dA идет на увеличение энергии, запасенной в конденсаторе. Суммируя работы по переносу заряда с ранее незаряженной обкладки, на вторую обкладку конденсатора мы вычислим тем самым и энергию зарядов, накопившуюся в конденсаторе.

(41) По (30) q=C и dq=Cd , поэтому (41) можно переписать

(42)

Выражение для энергии, запасенной в конденсаторе, (42) с учетом определения емкос­ти (30) можно записать

. (43)

Все эти выражения совершенно равноправны. Выражение для энергии, запа­сенной в конденсаторе, можно было бы получить, воспользовавшись выражением (27).

15. Энергия электрического поля

При зарядке конденсатора мы тратим энергию на создание внутри этого кон­денсатора электрического поля. Поэтому энергия, запасенная в заряженном конденсаторе, является энергией, существующего в нем поля. Попробуем вычислить объемную плотность энергии этого поля , т.е. энергию, приходящуюся на единицу объема поля. Сделаем это на примере плоского конденсатора. Под­ставим в выражение для энергии плоского конденсатора (42) его емкость (33)

Домножив в последнем выражении числитель и знаменатель на d, получим в числителе Sd=V объем, занимаемый полем, а его напряженность Е найдется как E= /d. В итоге получаем

Объемную плотность энергии поля получим, разделив W на V,

(44) В случае однородного поля его энергию можно подсчитать, умножив  на объем V , занимаемый полем

(45) Для неоднородного поля приходится разбивать объем, занимаемый полем, на достаточно малые объемы dV, такие, чтобы в их пределах можно было бы считать поле однородным. Энергия такого участка поля , и энергия всего поля найдется путем суммирования dW

(46)

16. Электрический диполь

Как мы уже говорили, электрическим диполем называют систему двух одинаковых по величине разноименных точечных зарядов: +q и -q, расстояние между которыми l значительно меньше, чем расстояние до тех точек, в которых определяется поле этой системы зарядов. Прямая, проходящая через оба заряда, называется осью диполя. Сам электрический диполь принято характеризовать его электрическим моментом р. Электрический момент диполя (его иначе называют дипольный момент) – это вектор, направленный от отрицательного заряда к положительному и модуль которого равен произведению q и l (рис. 13).

р = ql

Поле диполя обладает осевой симметрией. Сориентируем диполь вдоль оси х (рис. 14), а ось у направим вдоль серединного перпендикуляра к l.

М

-q q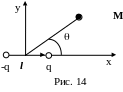

l p

Рис. 13

В случае, когда М находится от диполя на расстоянии r, значительно превы­шающем l, можно для потенциала диполя записать:

, (47)

для модуля вектора Е

. (48) Как видно из (47) потенциал поля диполя убывает с расстоянием быстрее, чем потенциал поля точечного заряда (1/r² вместо 1/r). Напря­жен­ность поля диполя также убывает быстрее (1/r³), чем напряженность по­ля точечного заряда (1/r²). Этого результата и следовало ожидать, на боль­ших расстояниях два заряда про­ти­воположных знаков кажутся столь близкими, что нейтрализуют друг друга.

В разных направлениях на одинаковом расстоя­нии от диполя Е имеет разные значения. При  = 0 (на оси диполя) мы получаем для

, (49) а для (перпендикулярно к оси)

. (50) Величины этих полей при одинаковом r отличаются в два раза.

Посмотрим теперь, как ведет себя диполь, помещенный в электри­ческое поле. Начнем с однородного поля (рис. 15). На заряды диполя со сто­роны поля действуют равные по величине, но противоположно направ­ленные силы f₁ и f₂.

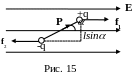
Эти силы образуют пару с плечом . Модуль каждой из сил равен qE. Момент этих сил, таким образом равен

(51) В векторном виде равенство (51) может быть записано

. (52) Этот момент сил стремится повернуть диполь так, чтобы дипольный момент уста­новился по направлению поля.

Если мы захотим увеличить угол между Р и Е на d, нужно совершить работу против электрических сил. Эта работа равна

(53) Совершенная работа увеличивает потенциальную энергию диполя в электри­ческом поле

(54) Проинтегрировав (54) и положив постоянную интегрирования нулю, получаем

. (55) Выбор константы интегрирования, равной нулю, означает выбор уровня отсчета потенциальной энергии. Она, таким образом, равна нулю, когда ди­поль перпен­ди­кулярен к полю. Эта энергия минимальна (-РЕ) для  = 180.

В связи с тем, что в неоднородном поле силы f₁ и f₂ не равны по модулю, кроме вращающего момента возникают еще силы, стремящиеся пе­ре­местить диполь в область с большим или меньшим значением напряженности.

Рассмотрим силы, действующие на диполь в неоднородном поле (рис. 16).

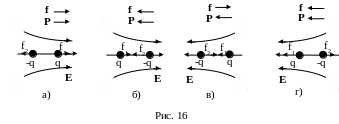
В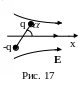 случае, когда Р сонаправлен с Е (а, г) результирующая сила f стремится вдвинуть диполь в область с более сильным полем. При Р, направленном против Е (б, в), сила двигает

диполь в область слабых полей.

Оценим теперь эту силу количественно

(рис. 17). Направим ось х вдоль изменения

электрического поля, совпадающего с Е в

месте нахождения диполя. Проекция силы f

на ось х может быть записана как

, (56)

откуда с учетом (55)

. (57)

Формула (57) естественно дает те же результаты, что и проведенные ранее ка­чест­венные рассмотрения. Для =0, f_x > 0 и направлена в положительном направ­ле­нии оси х. Эта сила втягивает диполь в область с большей Е. Для  = 180, f_x < 0 и диполь выталкивается в область слабых полей.