7. Работа электрических сил при переносе заряда

в электрическом поле

П

r

F

усть заряд q (рис. 6) создает электростатическое поле, а пробный заряд q’ надо переместить из точки 1 в точку 2. Работа по перемещению заряда из точки 1 в точку 2 определяется выражением:

2

1

dr

(8)

q

Рис. 6

Скалярное произведение векторов и можно представить в виде:

(9)

Подставив (9) в (8) и произведя интегрирование, получим

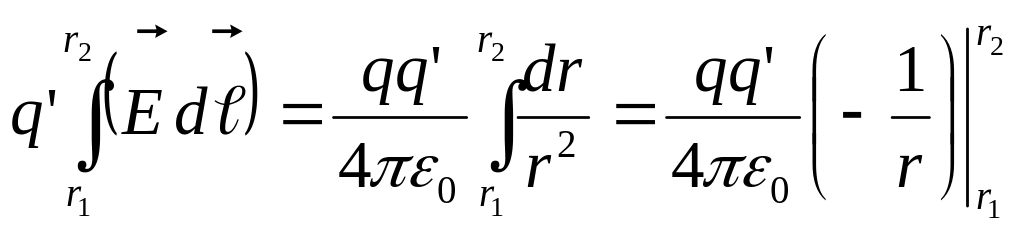
Итак, работа по перемещению q' из 1 в 2 имеет вид:

(10)

Из (10) следует два очень важных вывода: во – первых, работа сил электростатического поля по перенесению заряда не зависит от формы траектории, а только от положения начальной и конечной точек; во – вторых, работа электростатических сил по замкнутому контуру равна 0.

Поля, работа которых по замкнутому пути равна нулю, или, что тоже самое, не зависит от формы перемещения между двумя точками поля, называются потенциальными. Электростатическое поле – тоже потенци­альное поле. Другим примером потенциального поля является грави­тационное поле.

Не следует думать, что любые поля являются потенциальными. Так поле трения – вовсе не потенциальное поле. Двигая тело в поле сил трения по замкнутой траектории, мы на каждом отрезке этой траектории совершаем отрицательную работу. Поэтому суммарная работа при таком переносе тела оказывается отрицательной. Придадим выражению (10) иное математическое выражение.

Поскольку работу сил электростатического поля на участке траектории dl можно записать, как , где – проекция сил электростатического поля на направление перемеще­ния заряда, то с учетом равенства нулю работы по замкнутому контуру

(11) Кружок поставленный на знак интеграла относится к пределам интегрирования и означает, что здесь речь идет о суммировании по замкнутой траектории. Математики договорились такой интеграл взятый по замкнутой кривой называть циркуляцией вектора, стоящего под знаком интеграла. Воспользо­вавшись определением напряженности электрического поля (2), соотношение (11) можно переписать и окончательно, разделив на q левую и правую части равенства получим

(12) Это утверждение означает, что циркуляция вектора Е по замкнутому контуру рав­на нулю и выражает то обстоятельство, что электростатическое поле является потенциальным полем. Равенство (12) является интегральной формой утвержде­ния о потенциа­ль­ности электрического поля.

8. Разность потенциалов. Потенциал электрического поля

Выделим в электрическом поле две точки 1 и 2 и перенесем некоторый заряд q из точки 1 в точку 2 (рис. 6). Работу сил электрического поля по такому переносу обоз­на­чим А₁₂.

Если мы будем переносить между этими точками другой заряд, то величина работы будет, естественно, другой. Но вот, что интересно. Хотя величина совершенной работы зависит от величины перенесенного заряда, но от­но­шение этой работы к величине перенесенного заряда уже не зависит от величи­ны переносимого заряда. Следовательно, это отношение является некой новой ха­рак­теристикой электрического поля.

Мало этого, поскольку работа А₁₂ не зависит от траектории переноса (10), то выше названное отношение будет характеризовать не все электрическое поле, а только его две точки 1 и 2, да к тому же оно будет однозначной характеристикой этих точек. Такую характеристику принято называть разностью потенциалов меж­ду точками 1 и 2 и обозначать как или .

Итак, обобщая уже сказанное, можно утверждать, что разностью потен­ци­алов между точками 1 и 2 электрического поля называют отношение работы, кото­рую совершают силы электрического поля по переносу заряда из точки 1 в точку 2 к величине перенесенного заряда

(13)

В качестве второй точки, в которую из данной точки переносится заряд, можно избрать какую-либо заранее выбранную точку. Ее можно выбрать либо в бесконечности, либо на поверхности Земли, либо в каком-нибудь другом месте. Можно подсчитать работу по переносу заряда из данной точки в эту заранее выбранную точку и, разделив эту работу на величину перенесенного заряда, мы получим величину, называемую потенциалом данной точки поля , относительно этой заранее выбранной точки. Так можно ввести понятие потенциала относительно бесконечности, потенциала, относительно Земли и т.п. В каждой конкретной задаче точку, относительно которой отсчитывается потенциал, можно выбирать заново исходя из условий задачи. Следует еще раз подчеркнуть, что, хотя мы и пользуемся в этих случаях понятием потенциал, но физический смысл этого понятия по-прежнему связан с разностью потенциалов. Под потенциалом точки поля имеется в виду разность потенциалов между данной точкой поля и какой-то заранее выбранной его точкой. Разность потенциалов, потенциал – энергетическая характеристика электрического поля.

Понятие разности потенциалов широко используется физиками по двум при­чинам. Во-первых, это величина, в отличие от напряженности поля, величина скалярная, а со скалярными величинами работать легче, чем с векторными. И во-вторых, приборы для измерения разности потенциалов имеют более простое уст­ройство и шире, в связи с этим распространены, чем приборы для измерения напряженности электрического поля.

Пользуясь определением понятия разности потенциалов, можно установить единицу для измерения этой величины. В системе СИ работа измеряется в джоу­лях, заряд в кулонах, поэтому за единицу разности потенциалов принимают раз­ность потенциалов между двумя точками поля в том случае, если для переноса заряда в 1 кулон между этими точками силами поля совершена работа в 1 джоуль. Эту единицу называют вольт (В).

1 В = 1 Дж/1 Кл

Мы уже сказали, что из-за того, что потенциал величина скалярная, многие математические преобразования с этой величиной проще осуществлять, чем с напряженностью поля. Убедимся в этом на примере поиска потенциалов системы зарядов.

Пусть эта система состоит из неподвижных точечных зарядов, создающих электростатическое поле. Ранее на примере этой системы мы сформулировали принцип суперпозиции электрических полей, используя напряженность поля (3). Для потенциала  этой системы зарядов в произвольной точке можно записать

(14) Здесь и т.д. – потенциалы поля, создаваемых в этой точке каждым из заряд­ов при отсутствии остальных. Разумеется, на этот раз речь идет об алгебраической сумме.

Убедиться в справедливости соотношения (14) можно на основании следующих рассуждений. Подсчитаем работу сил электрического поля по переносу заряда q из данной точки поля, в какую-то заранее выбранную точку. Эта работа может быть представлена как сумма работ, совершаемых силами полей, создаваемых каждым из зарядов источников в отдельности

(15) Разделив равенство (15) почленно на величину переносимого заряда q получим утверждение (14).