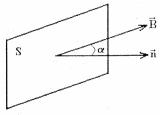
9.Магнитный поток.

Если поместить в однородное магнит­ное поле некоторую площадку (рис.52), то магнитным потоком или потоком вектора магнитной индукции, называют величину . Магнитный по­ток

в СИ измеряется в веберах (Вб). В неоднородном магнит­ном поле . Поскольку линии магнитной индукции являются замкнутыми линиями из-за отсутствия в природе маг­нитных зарядов,

то поток вектора магнитной индукции через замкнутую поверхность равен нулю . Дифференциальная форма записи этого утверждения divB=0.

10.Магнитное поле в веществе.

В веществе, помещенном в магнитное поле, индукция этого поля отличается от индукции магнитного поля в вакууме. Еще в XIX в. это обстоятельство было объяснено гипотезой Ампера о намагничивании веществ (магнетиков). По Амперу, в каждом веществе имеются круго­вые молекулярные токи. В отсутствие внешнего магнитного поля они ориентированы хаотически, беспорядочным образом, поэтому их результирующее магнитное поле равно нулю. Под действием внешнего поля моменты этих токов приобретают преимущественную ориентацию в направлении внешнего поля. Суммарный магнитный момент вещества становится отличным от нуля, а поля молекулярных токов уже не компенсируют друг друга. Поле в веществе с этих позиций равно , где – поле, созданное токами проводимости в вакууме, а – поле молекулярных токов. Поскольку линии индукции любых токов замкнутые, поток вектора В через замкнутую поверхность, как и в вакууме, остается равным нулю. (дифференциальная форма divB=0). Теорема о циркуляции вектора В изме­няется. Теперь циркуляция вектора В по замкнутому контуру определяется не только токами проводимости ( ), но и моле­кулярными токами ( ). Теорема о циркуляции магнитной индукции приобретает вид .

Это приводит к тому, что для расчета В с помощью этой теоремы необходимо знать не только распределение в про­странстве токов проводимости, но и распределение молекуляр­ных токов. Между тем можно для описания магнитного поля в веществе ввести вспомогательную величину, для расчета кото­рой достаточно иметь лишь информацию о распределении то­ков проводимости, а по этой величине уже рассчитывать В. Эта величина получила название «напряженность магнитного поля». , где – вектор намагниченности магнетиков (суммарный магнитный момент единицы объема вещества). Для большинства магнетиков вектор намагниченности прямо про­порционален Н. , – магнитная восприимчивость вещест­ва. В этом случае В и Н связаны соотношением ( – магнитная проницаемость вещества, ).

Для напряженности магнитного поля теорема о циркуляции имеет вид: циркуляция напряженности магнитного поля по замкнутому контуру равна сумме токов проводимости (макро­скопических токов), протекающих через площадку, ограничен­ную этим контуром

В дифференциальной форме теорема имеет вид rotH=j, где j – плотность тока проводимости.

На плоской границе раздела двух магнетиков вектора В и Н преломляются. Между тангенциальными и нормальными этих векторов выполняются следующие соотношения

Соотношения для нормальных составляющих выполняются при отсутствии токов проводимости на границе раздела.

Наклон линий индукции изменяется следующим образом (рис.50).

При переходе в магнетик с большей магнитной проницае­мостью линии индукции сильнее отклоняются от нормали. Это обстоятельство используют для формирования магнитных по­токов и защиты от воздействия внешних магнитных полей. Для

защиты от магнитных полей защищаемый объект окружают толстым ферромагнитным (большая ) экраном. Это снижает поле внутри экрана, но не ликвидирует его полностью. Полно­стью защитить какой-либо объект от воздействия магнитных полей можно лишь окружив его сверхпроводящим экраном.