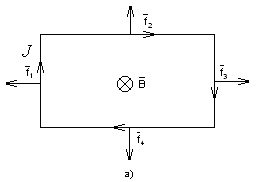
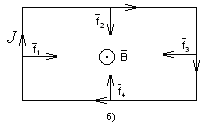
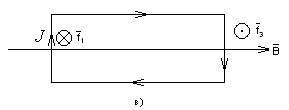
7. Контур с током в магнитном поле.

Магнитное поле ока­зывает силовое воздействие на замкнутый контур с током, ко­торый в него помещен. Проще всего проследить за этим воз­действием на примере прямоугольного контура. В случае а) (рис.44) на стороны контура действуют силы, стремящиеся его растянуть. В случае б) – сжать. При иных направлениях маг­нитного поля (например, рис. 44в) возникает момент сил М, стремящийся изменить ориентацию контура. Для модуля мо­мента сил в этом случае получается выражение М=РmВ, где Рm=I*S (S – площадь, охватываемая контуром), носящее назва­ние «магнитный момент тока». Вектор магнитного момента направлен по положительной нормали к контуру. Ее направле­ние определяется правилом правого буравчика: если вращать рукоятку буравчика по току, то поступательное движение буравчика укажет направление положительной нормали к контуру. В общем случае момент сил, действующих на контур с током, определяется соотношением М=[Рm,В].

Для того чтобы угол между векторами Pm и В увеличить на , надо совершить против сил, действующих на контур в поле, работу . Эта работа идет на увеличение энергии W, которой обладает контур в магнитном поле. Эта энергия равна W= –(Pm, B). При этом отсчет энергии начинается от энергии контура, расположенного так, что Pm параллелен В. Минимумом энергии контур обладает тогда, когда Pm направ­лен вдоль В (устойчивое положение равновесия), максимум – когда Pm направлен против В (неустойчивое положение равно­весия).

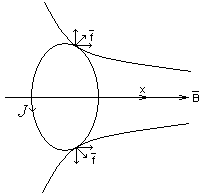
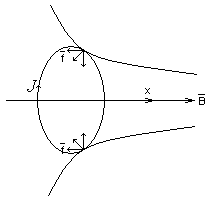
При внесении контура с током в неоднородное магнитное поле возникают силы, стремящиеся втянуть его в область про­странства с большим значением В (рис. 45а) или вытолкнуть в область с меньшим В (рис. 456).

Эту компоненту силы можно оценить количественно. Если неоднородность поля направлена вдоль оси х, то . При контур втягивается в магнитное поле, при – выталкивается из него.

а)			б)

8.

Циркуляция вектора магнитной индукции.

Описанная теорема дает одно из фундаментальных свойств магнитного поля – его вихревой характер. Этим магнитное поле отличается от электростатического, имеющего безвихревой, потенциальный характер. В вакууме теорему о циркуляции магнитного поля формулируют для вектора магнитной индук­ции. Циркуляция вектора магнитной индукции прямо пропорциональна алгебраической сумме токов, протекающих через площадку, ограниченную этим контуром .

В магнетиках попытка записи теоремы о циркуляции магнитной индукции приводит к тому, что в правой части теоремы фигурируют суммы макроскопических (обычных) токов и микроскопических, связанных с гипотезой Ампера о причинах намагничивания магнетиков. Чтобы избежать этого, вводят вспомогательную характеристику магнитного поля, называемую его напряженностью. . Здесь J – вектор намагниченности, а μ – магнитная проницаемость магнетика. Для напряженности магнитного поля в веществе теорема о циркуляции имеет вид:

, т.е. циркуляция вектора напряженности определяется только суммой макроскопических токов.

В соответствии с теорией электромагнитного поля, разви­той Максвеллом, магнитное поле может быть создано не только токами прово-димости, но меняющимися электрическими поля­ми, поэтому для переменных полей теорема о циркуляции при­обретает вид , где – поток вектора электрической индукции через площадку, ограниченную кон­туром, по которому ищется циркуляция Н. Величину называют током смещения.

Дифференциальные формы записи теоремы о циркуляции имеют вид .