2.1. Максиминный критерий Вальда.

Согласно этому критерию, гарантируется опред. выигрыш при наихудших условиях. Критерий основывается на том, что если состояние природы неизвестно, то нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы, т. е. в каждой строке матрицы находится минимальный элемент:

, i=1,m

Оптимальное значение системы:

_{K(оптим-ое) = max } K(Ai), i=1,m 

или.

Если руководствоваться этим критерием, нужно всегда ориентироваться на худшие условия и выбирать ту стратегию, для которой в худших условиях выигрыш максимален.

2.2. Критерий минимаксного риска Сэвиджа.

Данныйкритерий минимизирует потери эффективности, при наихудших условиях. Для оценки системы на основе данного критерия матрица эффективности должна быть преоюразована в матрицу потерь. Каждый элемент данной матрицы определяется следующим образом: определяется как разница между максимальным и текущим значением оценок эффективности по столбцу.

дельта - ( - текущее значение по столбцу)

После преобразования матрицы используется критерий минимакса,то есть находится минимальное значение из полученных максимальных.

Этот критерий рекомендует в условиях неопределённости выбирать ту стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации (т.е. тогда, когда риск максимален):

Сущность этого критерия состоит в том, чтобы любыми путями избежать большого риска при принятии решения.

Критерии Вальда и Сэвиджа относятся к группе критериев крайнего пессимизма.

2.3. Критерий пессимизма–оптимизма Гурвица (критерий обобщенного максимина)

Согласно данному критерию при оценке выбора систем не разумно проявлять как осторожность, так и азарт, а следует учитывать самое высокое и самое низкое значение эффективности и занять промежуточную позицию. Для этого выводится коэф. оптимизма – d принадлежащий интервалу (0,1),характеризующий отношение лица, принимающего решение к риску.

По критерию Гурвица, оптимальной является та стратегия   для которой принимает наибольшее значение величина

*(1-d) + d* max aij, i=1,m

_{K(оптимальное) = max } K(Ai), i=1,m 

24. Ф-ия риска.

Если построить график ф-ии риска, то это будет некоторая кривая с явным экстремумом (типа параболы).

ρ*(ᵞ)= ᵞ wα(ᵞ)+(1-ᵞ)β(ᵞ)

w-потери

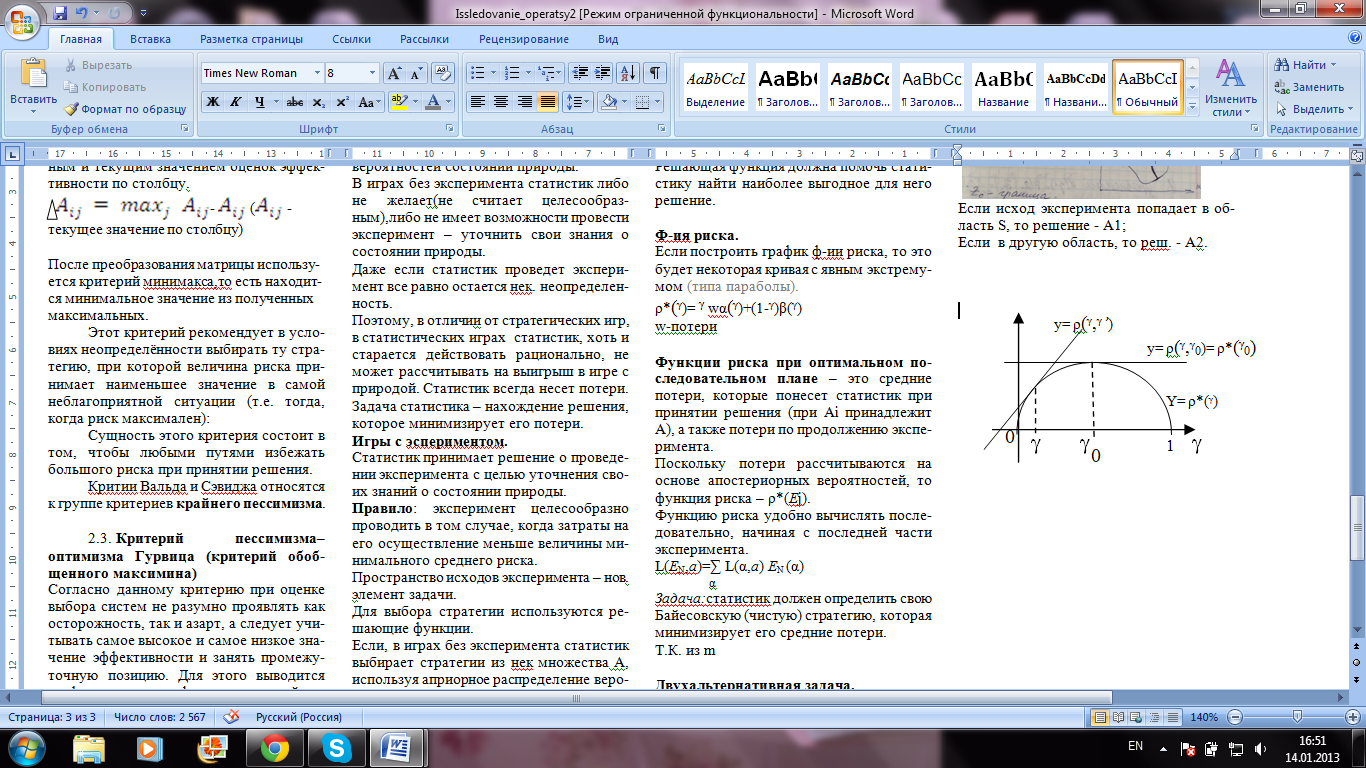
Точка гамма нулевое - это точка, где потери статистика набольшие. Функция риска является функцией распределения вероятностей состояний природы.

Значение функции риска(потери статистика) будет зависеть от того, с какой точностью мы определили значение гаммы.

Поэтому применение байесовского принципа в задачах допустимы в тех случаях, если мы уверены в точности определения априорного распределения вероятностей.

Если уверенности нет, то применение байес. Действия может дать неудв. результат => принцип minmax

Функции риска при оптимальном последовательном плане – это средние потери, которые понесет статистик при принятии решения (при Ai принадлежит А), а также потери по продолжению эксперимента.

Поскольку потери рассчитываются на основе апостериорных вероятностей, то функция риска – ρ*(Ej).

Функцию риска удобно вычислять последовательно, начиная с последней части эксперимента.

L(EN,a)=∑ L(α,a) EN (α)

α