1. Ценность ресурсов

Двойственные оценки ( , y₄) отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности.

Примечание. Ценность различных видов сырья нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность сырья только относительно полученного оптимального решения.

Теневые цены ресурсов показывают, какие ресурсы являются более дефицитными, какие менее и какие совсем недефицитные (избыточные).

В нашем примере, объективно обусловленные оценки (ячейки E14:E17):

• оценка ресурса «труд» равна ;

• оценка ресурса «сырье1» равна ;

• оценка ресурса «сырье2» равна ;

• оценка ресурса «оборудование» равна .

Вычислим значение целевой функции двойственной задачи:

т.е.

Теорема 1 (основная теорема двойственности).

Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций задач равны:

Если одна из двойственных задач неразрешима, то неразрешима и другая.

ВЫВОД: По первой теореме двойственности мы можем утверждать, что действительно найдены оптимальные значения двойственных переменных.

2. Анализ использования ресурсов в оптимальном плане выполня­ется с помощью соотношений 2-й теоремы двойственности.

Теорема 2 (о дополняющей не жесткости)

Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i-е ограничение обращается в неравенство, i-я компонента оптимального плана двойственной задачи равна 0.

Если i-я компонента оптимального плана двойственной задачи положительна, то ее i-е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.

Дефицитные ресурсы, полностью используются в оптимальном плане , имеют положительную оценку .

В примере «труд» и «сырье 2» - дефицитные ресурсы:

«труд» -

«сырье 2» -

Чем выше величина оценки , тем острее дефицитность i-го ресурса.

ВЫВОД: В примере «труд» более дефицитен, чем «сырье2»: , следовательно, его дефицитность ощущается острее и увеличение ресурса наиболее выгодно.

Не полностью используемые ресурсы (для которых ), имеет нулевую оценку

В примере «сырье1» и «оборудование» не является дефицитные ресурсом:

«сырье1» -

«оборудование» -

ВЫВОД: Ресурс недефицитен не из-за его неограниченных запасов (они ограничены величиной bi), а из-за невозможности его полного использования в оптимальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производства им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию f(X).

3. Максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального решения, т.Е. Номенклатура выпускаемой продукции, остается без изменений.

Для ответа на данный вопрос вернемся к отчету по устойчивости:

Рис.10. Отчет по устойчивости анализ изменения запасов сырья.

• Запас ресурса «труд» изменяется в диапазоне: 1620 ≥ «труд» ≤ 2200;

• Запас ресурса «сырье1» изменяется в диапазоне: 12600 ≥ «сырье1» ≤ +∞

• Запас ресурса «сырье 2» изменяется в диапазоне: 6667≥ «сырье 2» ≤8667

• Запас ресурса «оборудование» изменяется в диапазоне: 550 ≥ «сырье 2» ≤+∞.

+∞ - означает, что изделие находится в избытке и изменение запасов сырья в сторону увеличения может быть бесконечным.

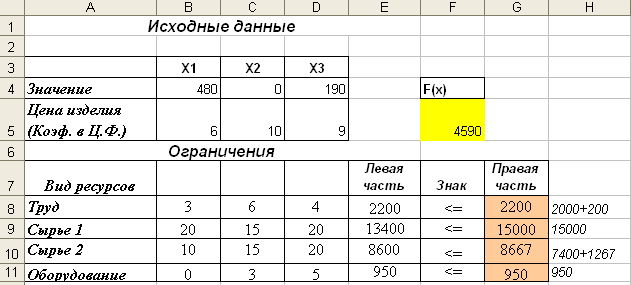
Рис.11. Изменения запасов сырья в сторону допустимого увеличения.

Проверьте правильность ваших выводов, внеся изменения в значения ячеек G8:G8 сначала на допустимое увеличение ресурсов, затем на допустимое уменьшение.

Запустите Поиск решения и укажите новые значения Номенклатуры выпускаемой продукции.

ВЫВОД: Если изменения сырья будет проведено в указанном диапазоне, то номенклатура выпускаемой продукции, останется без изменения.