Лабораторная работа №4

Тема: "Оптимизационные модели"

Цель работы: Научиться использовать электронные таблицы для выбора оптимального решения поставленной задачи и проверки правильности построения математической модели.

В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).

Рассмотрим пример задачи линейного программирования

Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице:

Вид ресурсов	Нормы расхода сырья на единицу продукции			Запасы ресурсов
	I вид	II вид	III вид
Труд	3	6	4	2000
Сырье 1	20	15	20	15000
Сырье 2	10	15	20	7400
Оборудование	0	3	5	1500
Цена изделия	6	10	9

1. Требуется найти такой план выпуска продукции, при котором будет максимальной общей стоимость продукции.

Обозначим через X₁ - количество изделий I вида, X₂ - количество изделий II вида, X₃ - количество изделий III вида.

Экономико-математическая модель задачи будет иметь вид:

Целевая функция – это выражение, которое необходимо максимизировать:

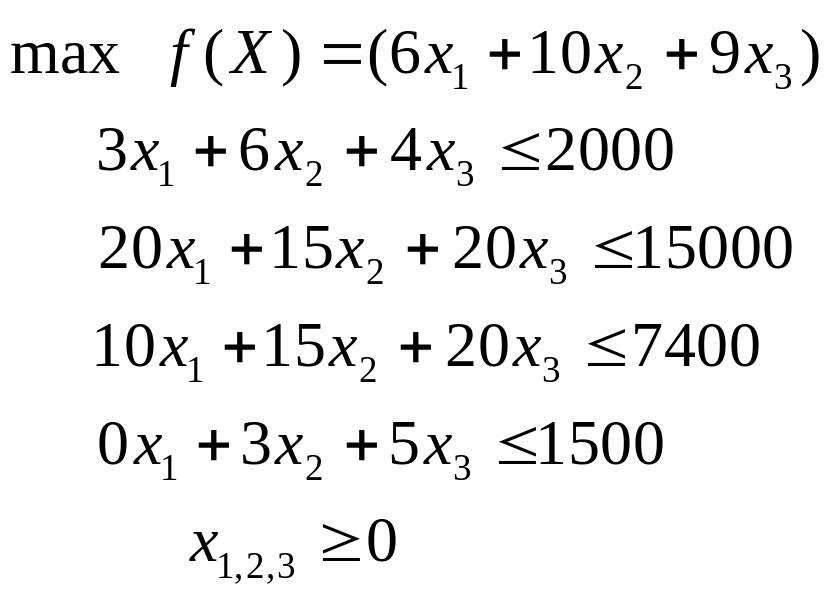Ограничения по ресурсам

В этой модели функциональные ограничения отражают условия ограниченности объемов используемых в производстве ресурсов.

Получим оптимальный план выпуска продукции, используя «Поиск решения».

Поиск решения - это надстройка EXCEL, которая позволяет ре­шать оптимизационные задачи.

Примечание. Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку, для этого выберите команду Сервис => Надстройки и активизируйте надстройку Поиск ре­шения.

Если этой надстройки нет в диалоговом окне Надстройки, то вам необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки EXCEL (или Office) установить надстройку Поиск решения.

Для решения задачи необходимо:

1. Создать форму для ввода условий задачи.

2. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).

3. Ввести исходные данные.

4. Ввести зависимость для целевой функции.

5. Ввести зависимости для ограничений.

6. Указать назначение целевой функции (установить целевую ячейку).

7. Ввести ограничения.

8. Ввести параметры для решения ЗЛП.

1. Подготовим форму для ввода условий1 (Рис.1)

Рис.1. Форма для ввода данных.

2. В нашей задаче оптимальные значения вектора X=(X₁, X₂, X₃) будут помещены в ячейках B4:D4, оптимальное значение целевой функции – в ячейке E5.

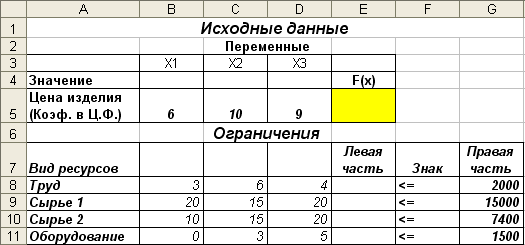
Рис.2. Данные введены.

2. Введем исходные данные в созданную форму. Получим результат, показанный на рис.2.

3. Введем зависимость для целевой функции (Рис. 3):

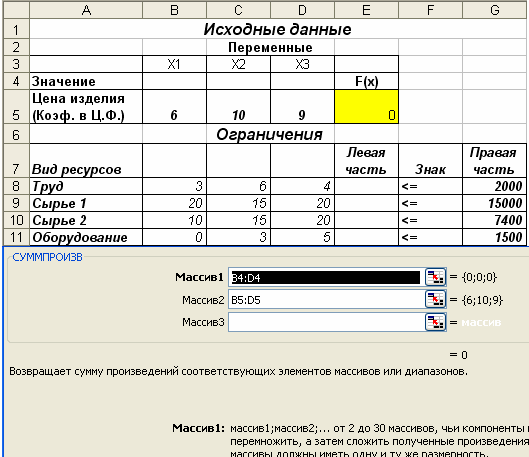
Рис.3. Вводится функция для вычисления целевой функции.

2. Введем зависимость для ограничений, для этого в ячейки E8, E9, E10 ,E11 соответственно:

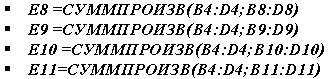
Запуск Поиска решения

После выбора команд Сервис =>Поиск решения появится диалоговое окно Поиск решения.

В диалоговом окне Поиск решения есть три основных параметра:

• Установить целевую ячейку

• Изменяя ячейки

• Ограничения

Сначала нужно заполнить поле «Установить целевую ячейку».

Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск наименьшего или наибольшего значения целевой ячейки или же установить конкретное значение.

Второй важный параметр средства Поиск решения - это параметр Изменяя ячейки.

Изменяемые ячейки - это те ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. Для поиска решения можно указать до 200 изменяемых ячеек.

К изменяемым ячейкам предъявляется два основных требования:

• Они не должны содержать формул;

• Изменение их значений должно отражаться на изменении результата в целевой ячейке.

Следовательно, целевая ячейка зависима от изменяемых ячеек.

Третий параметр, который нужно вводить для Поиска решения - это Ограничения.

2. Назначение целевой функции (установить целевую ячейку).

• Курсор в поле «Установить целевую ячейку».

• Ввести адрес $E$5.

• Ввести направление целевой функции: Максимальному значению.

Ввести адреса искомых переменных:

• Курсор в поле «Изменяя ячейки».

• Ввести адреса В$4:D$4.

2. Ввод ограничений.

• Курсор в поле «Добавить». Появится диалоговое окно Добавление ограничения (Рис. 4).

• В поле «Ссылка на ячейку» ввести адрес $E$8.

• Ввести знак ограничения ≤.

• Курсор в правое окно.

• Ввести адрес $G$8.

• Добавить. На экране опять диалоговое окно Добавление ограничена.

• Ввести остальные ограничения.

• После ввода последнего ограничения ввести ОК.

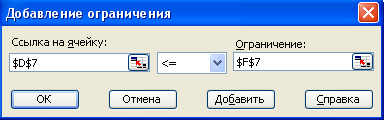
Рис. 4. Ввод правых и левых частей ограничений.

На экране появится диалоговое окно Поиск решения с введенными условиями (Рис.5).

8. Ввод параметров для решения ЗЛП (Рис. 6).

• Открыть окно Параметры поиска решения.

• Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.

• Установить флажок Неотрицательные значения.

• ОК. (На экране диалоговое окно Поиска решения).

• Выполнить. (На экране диалоговое окно Результаты поиска решения – Рис. 7).

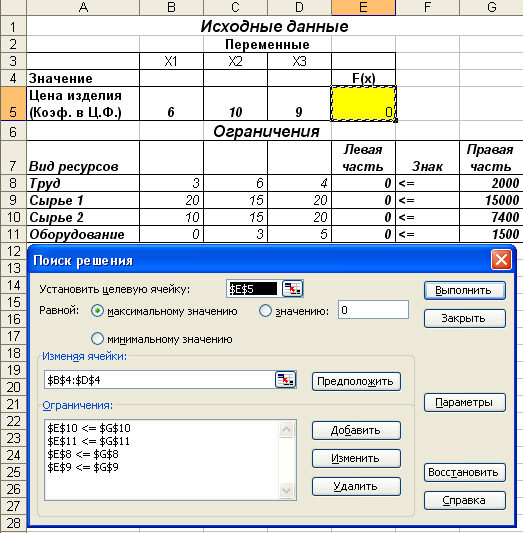
Рис. 5. Введены все условия для решения задачи.

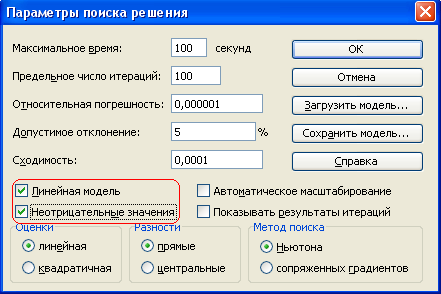
Рис 6. Ввод параметров.

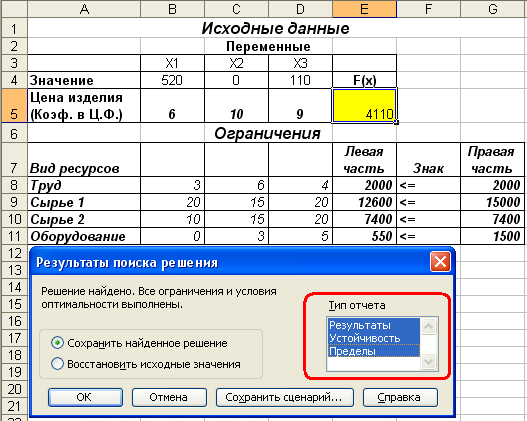
Рис.7. Решение найдено.

Полученное решение означает:

1. Максимальный доход – 4 110 тыс. руб. предприятие получит при выпуске 520 единиц изделий I вида (X₁ ) и 110 единиц изделий III вида (X₃).

Создание отчета по результатам поиска решения

EXCEL позволяет представить результаты поиска решения в форме отчета. Существует три типа таких отчетов:

Результаты (Answer). В отчет включаются исходные и конечные значе­ния целевой и влияющих ячеек, дополнительные сведения об ограничениях.

Устойчивость (Sensitivity). Отчет, содержащий сведения о чувстви­тельности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.

Пределы (Limits). Помимо исходных и конечных значений изме­няемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

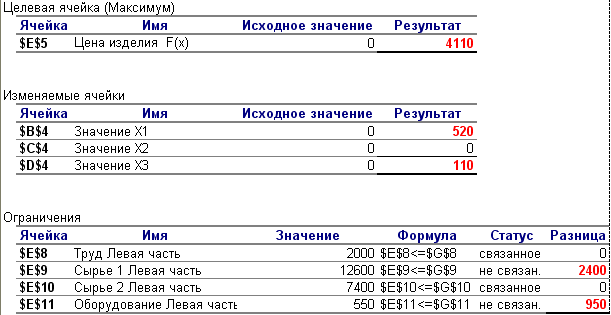
Рис. 8. Отчет по результатам.

В отчете по результатам содержаться оптимальные значения переменных X₁, X₃, которые соответственно равны 520 и 110, значение целевой функции – 4110, а так же левые части ограничений.

Проанализировав Отчет по результатам можно сделать следующие выводы:

1. Трудовые ресурсы и Сырье 2 будут использованы полностью.

2. Сырье 1 будет израсходовано 12600 ед. из 15000 единиц, имеющихся в наличии, остаток на складе составит 2400 ед.

3. Ресурсы Оборудование будут использованы 550 ед. из 1500 единиц, имеющихся в наличии, невостребованными окажутся 950 ед. оборудования.