
2 У равнение Бернулли
При движении жидкости по трубопроводу без дополнительного подвода
энергии (источника работы или тепла) или ее отвода удельная энергия жидкости по закону сохранения энергии не будет изменяться. Поэтому при перемещении жидкости от некоторог о сечения I—I до сечения II—II (рис. 6-
7) удельные энергии жидкости в этих сечениях будут одинак овы:
g
p
u
g
p
2
1
1
2

![]()
z w2 .
1 1 2 2 2 2 2
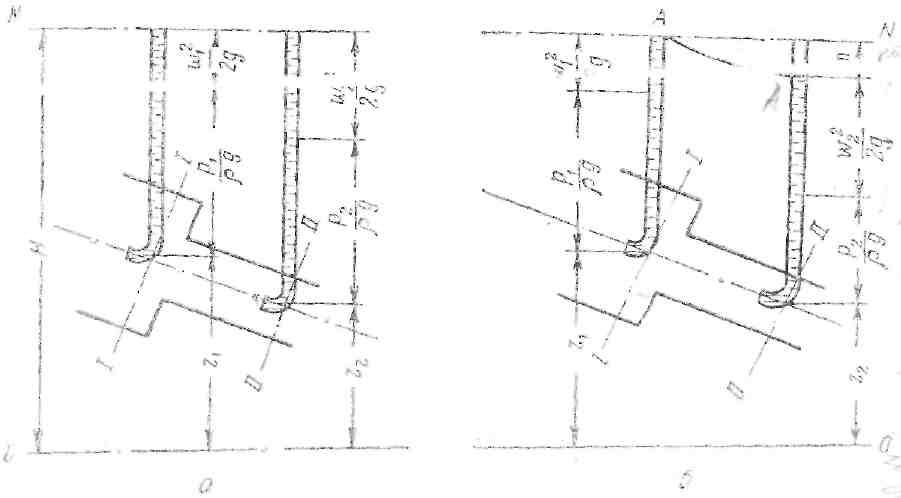
6-7. Графическое изображение уравнения Бернулли:
а — для идеальной жидкости; б — для реальной жидкости

g
u
g
2
1
2


z w1
p2 z
2
w
1 1 2 2 2 2
I) Рассмот рим движ ение идеальной к апельной ж идк ости (ри с. 6-7, а) , для
.
2
1
 к
оторой,
к
ак
и
для
любой
к
апельной
ж
идк
ости,
Идеальная
к
оторой,
к
ак
и
для
любой
к
апельной
ж
идк
ости,
Идеальная
жидкость движется без трения , поэтому, при отсутствии подвода тепла, ее температура и внутренняя энергия не будут изменяться. Следовательно, в
u
2 . Тогда уравнение энергетического баланса примет вид:
z
g
w
2
g
2
(6-28)
1 2 g 2 2 g
 Это
уравнение,
выражающее
энергетический
баланс
движущейся
идеальной
жидкости,
называется
уравнением
Бернулли.
(У
равнение
(6-28)
получается
делением
на
g
обеих
частей
уравнения
(6-27),
выражающег
о
энергетический
баланс
1
кг
жидкости,
и,
следовательно,
представляет
собой
энергетический
баланс
1/g
кг
жидкости.).
Это
уравнение,
выражающее
энергетический
баланс
движущейся
идеальной
жидкости,
называется
уравнением
Бернулли.
(У
равнение
(6-28)
получается
делением
на
g
обеих
частей
уравнения
(6-27),
выражающег
о
энергетический
баланс
1
кг
жидкости,
и,
следовательно,
представляет
собой
энергетический
баланс
1/g
кг
жидкости.).
В уравнении (6-28) член z, выражающий потенциальную энергию положения жидкости, имеет размерность длины и называется геометрическим напором.
g Член
p выражает
потенциальную
энергию
давления
жидкости
и
также
Член
p выражает
потенциальную
энергию
давления
жидкости
и
также
имеет размерность длины:
 н
н
к
g
г м
г м
к
кг м
м3 с 2
м3 с 2
Энергия давления может быть измерена при помощи вертикальной пьезометрической трубки. Под действием давления жидкость поднимается в
g трубке
на
высоту
h
трубке
на
высоту
h
p , которая называется пьезометрическим, или
статическим напором.
 2
2
Член
w выражает удельную кинетическ ую энергию движущейся
2g
жидкости. Этот член, называемый скоростным, или динамическим напором,
также имеет размерность длины:
 м2
м2
2
с
g м
с 2
Скоростной напор равен высоте, на которую может подняться струя жидкости, вытекающей вертикально вверх с начальной скоростью w.
Таким образом, согласно уравнению Бернулли, при движ ении идеальной
ж идкости сумма геометрического, пьезометрического и скоростного
напоров во всех сечениях потока является постоянной величиной.
II) Рассмот рим уравн ение Берн улли для реальной ж идк ости, движ ущейся
с трением. В этом случае при переходе жидкости от сечения I—I до сечения II—II (рис. 6-7,б) часть удельной энергии будет расходоваться на преодоление трения и других сопротивлений. Потерянная при этом энергия
.
2
1
gz1
g
2
2 2
u
2
2
u
u
В уравнении (6-29) член
u2 1 выражает увеличение внутренней энергии
1 кг жидкости и равен удельной энергии, затраченной на преодоление сопротивлений между сечениями трубы I—I и II —II. Таким образом, после деления уравнения (6-29) на g, уравнение Бернулли для реальной жидкости можно написать в следующем виде:
h
z
g
g
w
2
2
p2 w2
. (6-30)
1
u где
hП
где
hП
2 g 2
u
g
2 g П
Член hП
как и другие члены уравнения (6.30), имеет размерность длины и
называется потерянным напором.
Таким образом, согласно уравнению Бернулли, при установившемся
движ ении реальной ж идкости сумма геометрического, пьезометрического, скоростного и потерянного напоров в каж дой точке любого сечения потока является постоянной величиной.
Все напоры имеют размерность длины, поэтому уравнение Бернулли наглядно представлено графически (см. рис. 6-7). Все напоры будут изображаться отрезками вертикальной прямой, а их сумма — вертикалью, проведенной от произвольно выбранной плоскости сравнения 0—0 (нулевой уровень) до общей горизонтальной плоскости N—N.
Если в рассматриваемых сечениях поместить открытые изогнутые стеклянные трубки, один конец которых направлен по оси потока, то высота подъема жидкости в трубках будет соответствовать сумме пьезометрического и скоростного напоров. Для реальной жидкости отрезок hп (см. рис. 6-7, б) будет характеризовать величину потерянного напора при ее движении от сечения I—I до сечения II—II.
Сумма геометрического, пьезометрического и скоростного напоров
называется ги д р о ди на ми ч ески м нап ор о м
Если соединить уровни жидкости в
стеклянных трубках, получим нисходящую линию A—А (см. рис. 6-7,6), которая называется линией гидродинамического напора, или линией падения напора.
Из рис. 6-7, б видно, что гидродинамический напор реальной жидкости уменьшается в направлении ее движения на величину напора, потерянного между начальным и конечным сечениями потока.
Уравнение Бернулли является выражением одного из важнейших законов гидравлики, так как решение ее основных задач связано с определением расхода энергии и вычислением работы или мощности. Пользуясь уравнением Бернулли, определяют скорость и расход жидкости, т. е. пропускную способность аппаратов и трубопроводов. При помощи этого
уравнения рассчитывают также время истечения жидкости и ее
полный напор.
О б о б щ е н н о е у р а в н е н и е Б е р н у л л и
В общем случае реальная жидкость движется по трубопроводу (рис. 6-8), на котором расположены насос (или компрессор) 1, потребляющий работу L, и источник тепла (теплообменник 2) при помощи которого к жидкости подводится тепло Q. При этом возможно возрастание энергии потока между сечениями трубопровода I—I и II—II.
Если при движении жидкости отсечения I—I до сечения II—II к ней подводятся работа L и тепло Q, то энергия жидкости на этом участке уве- личится на L + Q. В этом случае энергетический баланс потока выражается уравнением
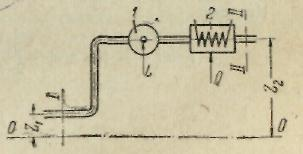
1 — насос или компрессор; 2 — теплообменник; L — работа; Q —тепло
L
E2 ,
(6-31)
где E1 и Е2 — полная энергия жидкости в сечениях I—I и II—II.
Выразив E1 и Е2 в соответствии с уравнением удельной энергии
жидкости (6-26) и разделив обе части выражения (6-31) на массу
g
l
w
q
1
w2
g
i2 z
2
,
z
2
,
2 2
(6-32)
где l
q
L подведенная работа, отнесенная к 1 кг жидкости;
 m
m
 Q
подведенное
тепло,
отнесенное
к
1
кг
жидкости.
Q
подведенное
тепло,
отнесенное
к
1
кг
жидкости.
m
Из уравнения (6-32) находим:
g

2 2
,
1
w
w
2
1
z
i1
q


z2 1
2 1 ,
2
(6-33)
Согласно уравнению (6-34), работа, сообщаемая движущейся жидкости, включая работу, эквивалентную количеству подведенного тепла, расходуется на повышение энтальпии жидкости, на ее подъем (преодоление силы тяже- сти) и на повышение кинетической энергии жидкости.
Обобщенное уравнение (6-34) может быть упрощено применительно к различным частным случаям, рассмотренным ниже.
Движение капельной (несжимаемой) жидкости. Для несжимаемой

1 2
.
u
w
2
получим;
p . Сделав подстановку в уравнение (6-33),
2

p2 gz 2
 2
2
p1 1
,
w
u

2
g
q
u
u2 1
hП . .
Поэтому
g
g
w
2
2

2
w
p
 1
z
1
1
z
1
1 2
g
(6-36)
или
2 2
z
p2 p1
w2 w1
g 2
2
hП , дж / кг
(6-37)
Таким образом, удельная работа l потребляемая насосом, расходуется на подъем 1 кг жидкости на высоту z2-z1, на повышение давления от p1 до р2 на увеличение кинетической энергии жидкости и на преодоление сопротивле - ний по пути движения жидкости.
Движение сжимаемой жидкости (газа). В большинстве случаев для газов, ввиду их малой плотности, можно пренебречь разностью высот z2 — z1, так как она мала по сравнению с другими членами уравнения энергетического баланса. Тогда общее уравнение (6-34) принимает вид
i1
q
(6-38)
2 2
w
w
 2
2
В этом уравнении l представляет собой работу, затрачиваемую на сжатие
1 кг газа (в компрессоре).
Пример 6-6. Вода в количестве V = 16 м3/ч подается под абсолютным давлением p1 = 3,5 бар (3,57 am) по магистральному трубопроводу диаметром d1 = 75 мм на охлаждение двух аппаратов I и II (рис. 6-9). Диаметр трубы d2 на ответвлении к аппарату I составляет 25 мм, на ответвлении к аппарату II d3 = 46 мм. Абсолютное давление воды на входе в аппарат I р2 = 3,35 бар (3,42 am). Разность геометрических высот z2 — z1 = H1 = 1,4 м. Определить скорость подачи и расход воды в каждом аппарате (сопротивле нием труб пренебречь).
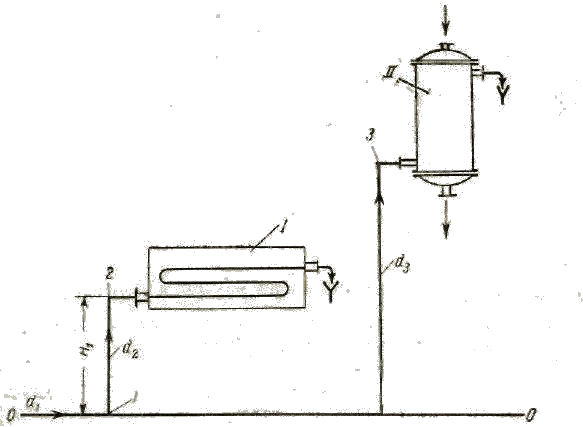
Р е ш е н и е . Принимаем за плоскость сравнения горизонтальную пло-
скость, проходящую через ось 0—0 магистрального трубопровода.
Уравнение Бернулли (6-28) для идеальной жидкости и точек 1 и 2:
z
w
p
g
z
3
p w2
g 2
2
.
2
2
.
2g
 Разность
статических
напоров
для
точек
1
и
2:
Разность
статических
напоров
для
точек
1
и
2:
1
g
3,5
,35
10 ,5 м.
1000
9,81
 где =
1000
кг/м3
(плотность
воды).
где =
1000
кг/м3
(плотность
воды).
Скорость воды в магистральном трубопроводе:
V
1
S1
V
d
3600 1
 4
4
3600
16
 0,785
0,785
1
Из уравнения (6-28) следует:
 2
2
2
2
(
g
w
2
p1 p2
w1 )2g
(
1
1
 ,4
,5
,4
,5
1 )2
 2
9,81
2
9,81
1
Расход воды на аппарат I:
 2
2
3
600 w2 S2
d2
3
4
3
3
1
м3 / ч.
3
1
V
V
I
6 3 м3 / ч.
Скорость воды в трубе-ответвлении к аппарату II:
w31
Vсек.
d
VII
1
3600 3
 4
4
3600
13
 0,785
0,785
2
