4 Материальный баланс потока (уравнения неразрывности потока)

Скорости движения частиц жидкости неодинаковы по сечению ее потока. Поэтому вводят понятие о средней скорости потока всех частиц жидкости в сечении. Допустим, что в сечении I—I трубы (рис. 6-5, а) все частицы имеют среднюю скорость w, тогда за единицу времени они пройдут путь, равный w, и переместятся в сечение II—II. Объем жидкости, протекающей в единицу времени через сечение I—I, будет равен объему V, заключенному между сечениями I—I и II—II, т. е. произведению средней скорости w на площадь поперечного сечения S потока.

Рис. 6-5. К выводу уравнений неразрывности потока

_{Это произведение представляет собой объемный расход жидкости:}

w

V S , м³ / с.

_(6-16)

_{откуда средняя скорость}

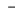_w ^V _{, м / с.}

S

(6-17)

Уравнение (6-16) носит название уравнения расхода. Скорость, входящая

в это уравнение, есть линейная скорость, т. е. путь, проходимый жидкостью в единицу времени.

Массовая скорость W представляет собой количество жидкости,

протекающее через единицу поперечного сечения потока в единицу времени, и определяется из соотношения

_W ^G _{, кг /( м}² _с).

S

(6-18)

где G — массовый расход жидкости, кг/с.

Зависимость между массовой и линейной скоростью можно установить,

_{заменив в выражении (6-18) G через V (где — плотность жидкости в}

кг/м³) и подставив вместо

^V _{его значение из равенства (6-17). Тогда}

^S

.

W w _(6-19)

Если скорости частиц жидкости не изменяются во времени, ее движение считается установившимся. При установившемся движении в каждом сечении потока постоянны не только скорость, но и расход, температура, давление и плотность жидкости. Вместе с тем при установившемся движении скорости потока могут изменяться в пространстве, при переходе жидкости от одного сечения к другому.

Рассмотрим установившееся движение жидкости, ограниченной стенками

любой формы, например движение в трубе переменного сечения (рис. 6-5, б). Движущаяся жидкость сплошь заполняет трубу, в которой, таким образом, нет пустот и разрывов потока. При переходе от сечения S₁ к сечению S₂ скорость жидкости будет изменяться, но по закону сохранения вещества количество жидкости, поступающей в единицу времени через сечение S₁, будет равно количеству ее, протекающему через сечение S₂, т. е. расход жидкости останется постоянным. В том случае, если эти количества не были бы равны (например, если поступающее через сечение S₁ количество жидкости превышало бы ее количество, проходящее через сечение S₂), жидкость накапливалась бы в трубе, между сечениями S₁ и S₂, и здесь происходило бы возрастание ее плотности и давления, что при установившемся движении невозможно.

S

Принимая массовые скорости жидкости в сечениях S₁ и. S₂ равными соответственно W₁ и W₂, можно написать

S

S

G или G

1^W1

S

1

₁^w₁

2^W2

c

2

c

₂ ^w₂

onst.

c

onst.

(6-20)

(6-21)

где ₁ и ₂ — плотности жидкости в сечениях S₁ и S₂.

^{Для несжимаемой жидкости} ₁ ⁼ ₂ ^{и уравнение (6-21) принимает вид}

S

S

^V ₁^w₁

₂ ^w₂

onst.

(6-22)

Уравнения (6-20) — (6-22) представляют собой материальный баланс

потока жидкости и называются уравнениями неразрывности потока.

Согласно этим уравнениям, средние скорости жидкости в различных сечениях трубопровода обратно пропорциональны площадям этих сечений. Произведение скорости на сечение, т. е. расход жидкости при установившемся движении, есть величина постоянная.