6.Определение доверительного интервала и доверительной вероятности по статистическим данным при интервальной оценке погрешности.

В отличие от точечной при интервальной оценке определяется доверительный интервал , в котором с доверительной вероятностью Р находится истинное значение :

.

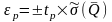При заданной вероятности Р и вычисленной 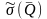значение t_P определяется законом распределения. В случае нормального распределения и числа измерений 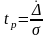выбирается по таблице функций Лапласа, при этом значения вероятности Р умножаются на 2, так как в табл. 2 они приведены для половины симметричного интервала.

Если число измерений , доверительный интервал случайной погрешности при заданных вероятности Р и СКО результата измерения определяется по формуле Стьюдента: ,

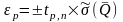где 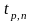– коэффициент распределения Стьюдента, который зависит от заданной вероятности Р и числа измерений n.

При распределение Стьюдента приближается к нормальному и вместо , можно использовать 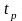для нормального распределения. При равномерном распределении обычно принимают , т.е. для 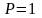, поскольку доверительный интервал слабо зависит от доверительной вероятности. Таким образом, истинное значение, очевидно, будет находиться внутри интервала: .

Можно также выразить относительную случайную погрешность 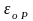, соответствующую доверительной вероятности Р, %, .

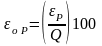Рассмотрим теперь, какую же доверительную вероятность следует брать? Как правило, принимают 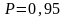. Если измерения нельзя повторить, то 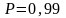, а в особо ответственных случаях, когда проводимые измерения связаны с созданием новых эталонов или имеют значение для здоровья людей, и выше.

В этих случаях при нормальном распределении доверительный интервал , что соответствует доверительной вероятности .

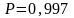7.Модель систематической погрешности. Не исключенные систематические погрешности. Пример.

Из-за различных знаков реализаций случайной погрешности случайная составляющая с ростом n уменьшается, а систематическая будет оставаться неизменной. Систематическая погрешность измерений может быть определена целиком, если выполнить измерение более точным методом с использованием более точных средств измерений. Значительно чаще приходится находить составляющие систематической погрешности, а затем их суммировать. Для этого необходимо глубоко понимать принцип работы средств измерений и физические процессы, протекающие в измерительных цепях. Полностью исключить систематическую погрешность введением поправки нельзя, поскольку поправка также определяется с некоторой погрешностью. Таким образом, всегда остаются не исключенные остатки систематической погрешности (НСП), которые обычно рассматриваются как случайные.

Заметим, что систематические погрешности могут быть связаны с каждым из элементов процесса измерений: несовершенством модели объекта измерения, несовершенством метода, средством измерения, изменением внешних условий, личными качествами наблюдателя.

Общие способы оценивания и исключения систематических

погрешностей

Для обнаружения, оценки и исключения систематических погрешностей требуется тщательное изучение применяемых конкретных методов, средств, условий измерения. Однако можно указать простейшие общие способы обнаружения, оценки и исключения систематических погрешностей.

1. Исключение систематической погрешности при измерении

путем применения соответствующих методов и приемов, например метода замещения, метода компенсации погрешности по знаку, использующего два измерения, в результаты которых систематическая погрешность входит с разными знаками и др. Эти методы позволяют исключить постоянную систематическую погрешность, обнаружение которой представляет наибольшие трудности, непосредственно в процессе измерения, а не путем обработки результатов.

2. Оценка систематической погрешности путем применения более

точного метода и средства измерения.

Систематическая погрешность, если пренебречь погрешностью сличения, будет равна 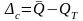, где 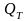– результат точного измерения.

3. Обнаружение систематической погрешности в результатах

измерений с многократными наблюдениями одной физической величины двумя независимыми методами. Для этой цели разработаны статистические методы обработки результатов, методы корреляционного и регрессионного анализа.

3. Оценивание систематической погрешности расчетным путем.

Для этой цели выражают значения измеряемой величины с учетом влияющего фактора («измеренное значение») и при его отсутствии («истинное значение»). Разность первого и второго значений и будет абсолютная систематическая погрешность .

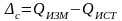5. Исключение систематической погрешности введением поправки.

Поправка 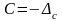бывает известна с ограниченной точностью и характеризуется средним значением 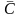со СКО 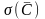. При введении поправки систематическая составляющая погрешности уменьшается, а дисперсия результата измерения возрастает. Критерием целесообразности введения поправки является интервал суммарной погрешности измерений. Если поправка не введена, интервал суммарной погрешности составляет 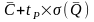, если введена –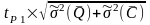 . 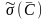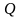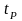Здесь и – оценки средних квадратических значений случайных погрешностей результата измерений величины и поправки , а и – величины, зависящие при одинаковой доверительной вероятности от законов распределения и . 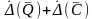Поправку необходимо вводить, если .

Отсюда получаем условие целесообразности введения поправки при :

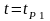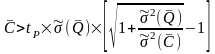. (7)