
- •1.Основные понятия метрологии. Измерения, истинное значение величины, абсолютная и относительные погрешности. Проблемы метрологии. Методы измерений.
- •2.Классификация погрешностей. Математические модели погрешностей.
- •3.Законы распределения случайных величин, при оценке погрешностей.
- •4.Математическая модель случайной погрешности. Числовые характеристики погрешности.
- •5.Определение случайной погрешности при известной функции распределения и ее параметров.
- •6.Определение доверительного интервала и доверительной вероятности по статистическим данным при интервальной оценке погрешности.
- •7.Модель систематической погрешности. Не исключенные систематические погрешности. Пример.
- •8.Метрологические характеристики. Нормированные метрологические характеристики.
- •9.Индивидуальные и типовые метрологические характеристики.
- •10.Нормирование инструментальной погрешности пределом допустимой погрешности. Достоинства и недостатки. Пример.
- •11.Расчет инструментальной погрешности в рабочих условиях. Пример.
- •12.Однократные измерения. Порядок проведения.
- •13.Расчет погрешности измерений с учетом методической погрешности.
- •14.Многократные измерения. Порядок выполнения многократных измерений с равноточными значениями отсчета. Оценка доверительного интервала доверительной вероятности.
- •15.Оценка инструментальной погрешности при многократных измерениях.
- •16.Погрешность измерения от вариации.
- •17.Погрешность косвенных измерений. Пример.
- •18.Расчет погрешности косвенных измерений по погрешностям прямых измерений. Пример.
- •19.Нормируемая метрологическая характеристика измерительных систем.
- •20.Оценка полной погрешности измерительных систем по характеристикам
- •21.Метрологическая служба. Меры обеспечения единства измерения.
- •22.Передача информации о размерах единиц рабочим средствам измерений.
- •23.Схема передачи информации о размерах и единицах. (Поверочная схема)
- •24.Стандартизация. Виды стандартов. Нормативные документы по
- •25.Гармонизация стандартов. Порядок разработки стандартов.
- •26.Стандарты качества.
- •27.Сертификация. Цели сертификации.
- •28.Схемы сертификации. Обязательная и добровольная сертификация.
- •29.Методы оценки соответствия при сертификации.
- •30.Виды контроля при сертификации продукции.
- •31.Методы проведения измерений при сертификации.
- •32.Система обеспечения качества на предприятиях.
- •33.Обеспечения качества в жизненном цикле продукции.
- •34.Методология управления качеством.
- •35.Качество сертификации. Исторические аспекты развития ксукп.
- •36.Автоматизированные системы в измерениях.
3.Законы распределения случайных величин, при оценке погрешностей.
Функция распределения.
Функция распределения вероятностей случайной величины:
 ,
,
которая выражает собой вероятность того, что случайная величина находится в интервале от – ∞ до некоторого значения, меньшего x1.
Функция
распределения любой случайной величины
является неубывающей функцией,
определенной так, что ,
а
,
а
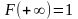 .
Вероятность того, что случайная величина
X
примет значение в интервале между x1
и х2,
равна:
.
Вероятность того, что случайная величина
X
примет значение в интервале между x1
и х2,
равна:
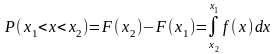 ,
(2)
,
(2)
Законы распределения случайных величин
Нормальное и равномерное распределения при проведении измерений встречаются наиболее часто.
![]()
Рис. 4.3. Равномерный закон распределения случайной погрешности Δ
При равномерном законе распределения случайная погрешность Δ принимает значения лишь в пределах конечного интервала Δ1 - Δ2 с постоянной плотностью вероятностей р(x). Математически равномерный закон выглядит так:
p(Δ)=с, при Δ1≤Δ≤Δ2 ;
p(Δ)=0, при Δ1>Δ>Δ2 , (4.8)
Площадь под кривой распределения равна единице: с(Δ2 - Δ1) = 1, отсюда
c=1/(Δ2-Δ1) .
Тогда (4.8) примет вид
p(Δ)=1/(Δ2-Δ1) , при Δ1≤Δ≤Δ2 ;
p(Δ)=0, при Δ1>Δ>Δ2 , (4.9)
Математическое ожидание и среднее квадратическое отклонение случайной погрешности Δ
M(Δ)=(Δ2+Δ1)/2 ;
σ=(Δ2-Δ1)/2√3 . (4.10)
Как уже указывалось, моды у равномерного закона распределения не имеется.
Нормальный закон распределения
p(Δ)=1/(σ√(2π))∙exp[-(Δ-M(Δ))/(2σ2)] . (4.11)
Как видно из (4.11), нормальный закон полностью характеризуется двумя числовыми характеристиками - математическим ожиданием и дисперсией. Колоколообразная кривая нормального распределения симметрична относительно оси ординат. Это означает, что погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто. Кроме того, малые погрешности встречаются чаще, чем большие. Данные свойства иллюстрирует рис. 4.4. Так, площадь под кривой плотности распределения вероятности в интервале Δ2-Δ1 существенно больше, чем площадь в равном интервале Δ4-Δ3. Площадь же под кривой плотности распределения вероятностей характеризует вероятность появления погрешностей.

Рис. 4.4. Вид нормального закона распределения случайной погрешности Δ
Рис. 4.5 иллюстрирует изменение формы кривой плотности распределения вероятностей при различных значениях средних квадратических отклонений (σ1>σ2>σ3). Видно, что чем большее значение имеет σ, тем больше результаты измерений рассеянны, тем больше вероятность проявления больших погрешностей. Таким образом, чем меньше значение σ, тем выше качество измерений.
4.Математическая модель случайной погрешности. Числовые характеристики погрешности.
Выше отмечалось, что измеряемая величина, содержащая случайную погрешность, должна рассматриваться как случайная величина. Напомним, что наиболее общей характеристикой непрерывной случайной величины X является плотность распределения ее вероятностей.
Плотность распределения вероятностей:
 ,
,
где
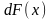 – вероятность значений случайной
величины x
в интервале dx.
– вероятность значений случайной
величины x
в интервале dx.
Наряду с плотностью распределения вероятностей используется функция распределения вероятностей случайной величины:
,
которая выражает собой вероятность того, что случайная величина находится в интервале от – ∞ до некоторого значения, меньшего x1.
Функция распределения любой случайной величины является неубывающей функцией, определенной так, что , а . Вероятность того, что случайная величина X примет значение в интервале между x1 и х2, равна:
, (2)
В практике электрорадиоизмерений чаще всего имеют дело с нормальным и равномерным распределениями.
Случайная величина X распределена нормально, если ее плотность вероятностей имеет вид:

где
σ
– среднее квадратическое отклонение
(СКО),
 – математическое ожидание.
– математическое ожидание.
Математическое ожидание М[Х] случайной величины X является постоянной величиной и характеризует ее среднее значение.
Величина
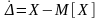 является случайной погрешностью. Если
систематическая погрешность отсутствует,
то математическое ожидание равно
истинному значению величины X.
является случайной погрешностью. Если
систематическая погрешность отсутствует,
то математическое ожидание равно
истинному значению величины X.
![]()
а) б)
Рис. 1
На
рис. 1,а показана дифференциальная
функция нормального распределения
f(x).
Видим, что с уменьшением σ уменьшается
рассеяние результатов вокруг X.
При расчетах используют нормированное
нормальное распределение, использующее
нормированную случайную величину
 :
:
 .
.
Интеграл
 выражает вероятность попадания случайной
погрешности в интервал
выражает вероятность попадания случайной
погрешности в интервал
 и носит название функции Лапласа. Из
таблицы значений функций Лапласа можно
найти, что вероятность появления
случайной погрешности в интервалах
и носит название функции Лапласа. Из
таблицы значений функций Лапласа можно
найти, что вероятность появления
случайной погрешности в интервалах
 с учетом симметричности распределения
равна соответственно 0,683, 0,954, 0,997. Эти
цифры характеризуют вероятность
появления случайной погрешности в
интервалах
с учетом симметричности распределения
равна соответственно 0,683, 0,954, 0,997. Эти
цифры характеризуют вероятность
появления случайной погрешности в
интервалах
 .
.
Нормальное распределение согласно центральной предельной теореме имеет сумма бесконечно большого числа бесконечно малых величин с любым законом распределения. На практике сумма сравнительно небольшого числа (4-5) статистически независимых величин одного порядка имеет распределение, близкое к нормальному. Если случайные погрешности определяются по результатам измерений, то погрешности в большинстве случаев имеют нормальное распределение.
Равномерное распределение, показанное на рис. 1,б, аналитически записывается в виде:

Вероятность
появления погрешности в интервале
 очевидно равна:
очевидно равна:
 .
.
Примером случайной погрешности, имеющей равномерное распределение, является погрешность отсчета по шкале прибора и погрешность квантования измеряемой величины по уровню в цифровых измерительных приборах. Равномерное распределение в пределах допускаемых границ приписывают погрешности измерительного прибора. Равномерное распределение принимают всегда, когда закон распределения неизвестен.
В
практике электрорадиоизмерений
встречаются и другие законы распределения.
ГОСТ 8.011 – 72 указывает функции
распределения, которыми следует
аппроксимировать реально имеющие место
законы. Это нормальная, равномерная,
треугольная, трапецевидная, антимодальные
I и II, Рэлея. Отношения максимальной
погрешности к СКО соответственно равны
 и
и
 .
.
Встречаются случаи, когда задача оценивания погрешности приводит к функции распределения, существенно отличной от указанных выше, так что ее неудобно аппроксимировать ни одной из них. В практике электрорадиоизмерений таким законом является, например, закон арксинуса (U-образное распределение).
Для характеристики случайных величин применяют также начальные и центральные моменты. Основными среди них являются математическое ожидание и дисперсия.
Математическое ожидание (первый начальный момент):
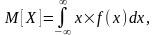
дисперсия (второй центральный момент):

Положительное значение корня квадратного из дисперсии и есть упоминавшееся выше среднее квадратическое отклонение
(СКО)
случайной величины .
.
Математическое ожидание, как отмечалось, является центром, относительно которого группируются значения случайной величины. СКО характеризует степень рассеяния значений случайной величины относительно математического ожидания.
Нормальное распределение полностью характеризуется математическим ожиданием М[Х] и СКО σ.
Равномерное
распределение (рис. 1,б) тоже определяется
двумя параметрами М[Х]
и
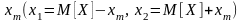 .
.
Дисперсия равномерного распределения:

а
среднее квадратическое отклонение: .
.
Вероятность
появления случайной погрешности в
интервале ±
σ
в соответствии с (2) составляет

