§1.5. Диаграмма деформации и дислокационная структура

ГЦК металлы. Цель изучения дислокационной структуры: поняв причины ее развития, суметь предсказать ее эволюцию в зависимости от условий и, как следствие, диаграмму деформации. Для монокри­сталла чистого металла с низкой начальной плотностью дислокаций Р~ 10⁵...10⁶см-² можно, выбрав ориентировку, начать с одной, первич­ной действующей системы скольжения (с наибольшим напряжением) и именно в ней наблюдать развитие дислокационной структуры. Карти­на четче для ГЦК металлов (где семейство скольжения единственное). В приведенных к первичной системе координатах (напряжение т_пь - сдвиг у_пЬ) на диаграмме растяжения т(у) ГЦК металлов в общем случае три стадии: две линейных и третья - с затухающим упрочнением. Эта тра­диционная классификация не включает "нулевой" стадии (с крутым упрочнением от порога упругости до текучести: у < Ю“³ %) и IV и V стадий больших деформаций у > 1, недостижимых при растяжении, но возможных при более мягком нагружении (кручении, прокатке, воло­чении).

Легкое скольжение. Первая стадия - текучесть (§1.2) при одинарном скольжении - легкое скольжение с низким упрочнением: на этой стадии нормированный на модуль сдвига G безразмерный модуль упрочнения 0] = D\!G - (dx/dy)/G для всех ГЦК металлов одинаково низкий: напри­мер, в меди [55] при 300 К 0i = (2...7) 10^-4 при пределе текучести x_s/G = (0,7...2,0) 10“⁵. Модуль упрочнения 0j зависит от ориентировки оси растяжения. Он наименьший (2 10^) в середине стереографического треугольника (см. рис. 9,6) - при наименьшем напряжении в конкури­рующей системе скольжения.

На первой стадии поверхность кристалла покрьюают параллельные следы одной системы скольжения - "атомнотонкие" (в плоскости сво­его источника), но макроскопической длины L ~ 1 мм при высоте h < 0,03 мкм (от п < 100 дислокаций). Они появляются "одномоментно" (позже не подрастают) и независимо друг от друга, постепенно и рав­номерно заполняяя весь объем. Плоскость скольжения почти пуста, и лишь редкие в ней жгуты дислокаций составляют основной прирост их плотности (§1.2). Слабое упрочнение - естественное следствие больших пробегов и малого накопления дислокаций.

Крутое упрочнение. Упрочнение резко меняется по достижении не­кой критической плотности линий скольжения (шаг Я <0,3 мкм) при деформации yi - nb/H -0,1. При этом сдвиг у₀, приводящий кристалл в симметричное положение (на оси [100] - [111] - рис. 9, в) еще не достиг­нут (при 300 К в наилучшей для одинарного скольжения ориентировке меди yi/yo ⁼ 0,2...0,4 [20]). Упрочнение изменяет не ориентировка, а "внутренняя" причина - созданная структура.

Одинарное скольжение накапливало дислокации в двух местах: жгу­ты на площадке скольжения и серии петель по ее периметру. В жгутах диполей дислокации разноименные, поэтому их дальнодействующее поле слабое. В серии петель дислокации одноименные и их поля скла­дываются: с удалением от периметра линии скольжения напряжения убывают (ч.1, с.204) как [т(х)/т]« 1 +(ZA)^1/2, пока расстояние x«L. При длине линий скольжения L и шаге Я среднее расстояние между их се- 38

риями дислокаций х ~ (ЬЩ^т. Тогда концентрация напряжений от них [т(х)/т]> 1+(L/Я)^1/4 [пятикратная при L~ 1 мм и 1 мкм (задача 28)] определяет ориентировку наибольших касательных напряжений и включает источники иных систем скольжения. Чем меньше сначала напряжения в иных системах скольжения, тем больше длина yi стадии легкого скольжения, но соответственно меньше модуль упрочнения 0ь так что упрочнение на I стадии Дт = Ayi мало зависит от ориентировки [56].

Когда накопление дислокаций вызовет множественное скольжение (в нескольких системах), это меняет формирование структуры и упроч­нение - начинается крутое упрочнение - II стадия диаграммы (рис. 14).

Местные поля серий дислокаций равно помогают (или мешают) источникам всех систем, поэтому первичная по-прежнему в выгодном положении: пока ориентировка далека от симметричной, скольжение в ней преобладает и на И, и на III стадиях [20] - ось растяжения 1 про­должает двигаться к тому же полюсу Ь.

t, МПа

Рис. 14. Диаграмма деформации монокристалла:

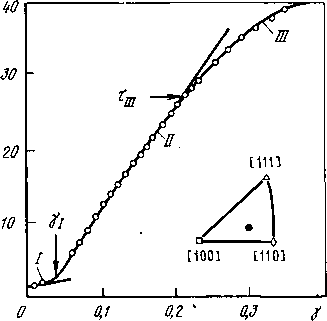
а - диаграмма растяжения моно­кристалла меди при 300 К со ско­ростью 410 с (ориентировка для одинарного скольжения, по­казана на стереографическом треугольнике) [20]; б - схема к определению параметров диа­граммы деформации на III стадии; в - зависимость модуля упрочне­ния 0 от напряжения течения t/G, видны шесть стадий диаграммы деформации

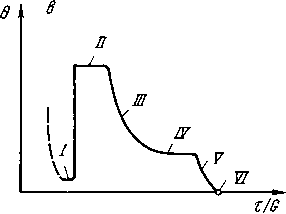
Рис. 15. Последствия вторичного скольжения в ячеистой структуре: а - сплетения дислокаций в первичной плоскости скольжения, ог­раничивающие пробег Z.2 во вторичной (по границам ячейки накап­ливается разворот со); б - эти скопления вследствие разворота вышли из плоскости скольжения, что ограничивает пробег U дис­локаций первичной системы скольжения

Судя по рельефу скольжения, и на II стадии линию скольжения соз­дают /1~ 20...50 дислокаций. Закрепив дислокации нейтронным облу­чением меди под нагрузкой, обнаружили в ориентированной фольге ("вид плашмя”) те же плоские серии 15...20 дислокаций от общего ис­точника [57]. С "торца" же вплоть до конца II стадии (при у = 0,43; р ~ Ю¹⁰ см^-2) видны плоские полосы скольжения первичной системы толщиной 0,2...0,6 мкм, длиннее кадра (8 мкм) и с разворотом приле­гающих объемов со-'0,2... 1 . После разгрузки столь строго плоских слоев дислокаций не видно.

Ячеистая структура. Дислокации иных систем скольжения, пересе­кая промежуток Н между первичными полосами, вступают в реакции с их дислокациями, и это ограничивает их пробег шагом полос Н (рис. 15). От этого первичные полосы скольжения, заполняясь дислока­циями по всей своей площади, оформляются в рыхлые границы ячеек,, имеющих поперечник Н. "Уплотнение" превращает их в плоские суб­границы с разворотом со, постепенно нарастающим до 1...2⁰, а ячейки - в свободные от дислокаций фрагменты толщиной d$ - Н~ 0,1 ...0,5 мкм.

Причина разворота оо₂ * У2 на границах фрагментов - накопление за­стревающих в первичной полосе одноименных дислокаций от сдвига уг во вторичной системе скольжения. Вторичное скольжение поворачива­ет "старые" полосы (как и всякие "метки" - см. §1.3) на угол оо₂ из пер­вичной плоскости скольжения (рис. 15). Теперь эти полосы ограничи­вают пробег дислокаций своей же, первичной системы: длина новых линий скольжения L\ = ///sina>₂ » #/оо₂. Вырезав из уже деформирован­ных образцов фольгу и продолжая растяжение с той же ориентировкой в микроскопе, видели in situ пробег дислокации L\ и измерили по сле­дам пробега угол со₂, В меди при растяжении вдоль оси [415] пробег L\ менялся от 300 мкм на I стадии до 10...50 мкм при со₂ - 1...3⁰ на III ста­дии [58].

Поскольку именно деформация II стадии в первичной системе yi = y-yi, вызывает де-

формацию во вторичной, следует ожидать q = 72/71 = const. Тогда длина "свежих" пер­вичных линий скольжения L\ = Hly2 = d^l[q(y-y\)\, должна убывать как Li = C/(y-yi). Действительно, измеряемая постадийно (при переполировках), их длина так и укорачи­вается с деформацией, доходя к концу II стадии до 10.. 25 мкм. Для разных металлов [20] почти одинаково С = 4...6 мкм (Си при 293 К, Ni при 90 К, Ni-20 % Со при 293 и 90 К). Отсюда следует q = d^JC < 0,1 - сдвиг от вторичного скольжения на порядок меньше, чем от первичного - преобладающего и на этой стадии.

В алюминии, судя по видеозаписи, всего по 1...2 дислокации, выйдя из границы, пробегают в ячейке 2...4 мкм до следующей границы и связываются в ней [44]. Чтобы из границы ячейки вышла и пересекла ячейку полупетля дислокации, нужно напряжение т/G ~b/d$. Для меди [59, 60] на II стадии измерено x/G = kb/d$ при к = 4,2...5,4, то есть с рос­том напряжения фрагменты измельчаются: ^ф~т^-1 как и в алюминии [61] (что напрашивалось и из соображений подобия: если для размно­жения дислокаций x/G-b/L, то в подобных структурах, созданных размножением, все характерные длины L ~ т^-1). При этом сохраняется подобие и в толщине границы В: в меди B/d$ «0,3 [62].

Модуль упрочнения. Подобием структур определяется и модуль уп­рочнения 0ц на II стадии. Если при плотности дислокаций р объем рав­номерно заполнен группами по п одноименных дислокаций, то среднее расстояние между группами г =_л/(л/р)- Касательные напряжения от них

т = k\nGb/2nr (геометрический множитель к\< 1 - для усреднения по ориентировкам). Приложенное напряжение должно преодолевать это сопротивление: т = k\Gb(pn)^m/2n.

Основное допущение подобия: если пробег L дислокаций от источ­ника ограничен другими источниками, то L = к₂ г - он пропорционален расстоянию между ними. Испуская п дислокаций, источник в объеме V совершает деформацию by-imL²b/V и дает приращение плотности

дислокаций 5р = 2imL/V и напряжений 5т = k\Gb(4n)(bJp)/2n - ⁼ k\Gb{ )5р/4тг_л/р . Отсюда 0ц = (8т/5у)/G = к\/2пк2 = const - модуль Упрочнения 0ц выражается комбинацией одних лишь геометрических постоянных. Для ГЦК металлов и сплавов 0ц * V300* Так, измерено ®п = (2,2...4,8) 10~³ (т. е. '/«„...V 210) для Al, Си, Ag, Аи, Ni и твердых рас­творов Ni-Co при (0,003...0,5)Гпл [20]. Это на порядок выше, чем на

1. стадии, где пробег дислокаций определяет их исходная плотность ро.

Как только главным фактором упрочнения станут поля вновь нако­ленных дислокаций, наступит II стадия - крутого упрочнения: напря­жение течения определяется плотностью этих дислокаций ^т ^ aGbу[р , (1.5.1)

^гДе а = ki(yf^)/2n - коэффициент, постоянный для данного типа струк- Т'Уры (данного п).

Но модуль упрочнения 0_П совсем не зависит от плотности дислока­ций р: все объемы - с малой и с большой плотностью дислокаций, - взаимодействуя, упрочняются одинаково. Границы ячеек -"источники и накопители" дислокаций - своим полем контролируют течение и внутри ячеек. Поэтому ячеистая структура, раз сформировавшись, со­храняет неравномерность распределения дислокаций между объемом и границей ячеек (до 1 : 5) при любой большой деформации. Из d_{ф - т^-1 и т = а Gb^fe видно соотношение подобия = const - измельчение

ячеек определяется плотностью дислокаций.

Если в приведенных координатах х(у ) модуль упрочнения 0ц постоянный, то на ма­шинной диаграмме растяжения <т(е) его аналог 0'ц = (da/ds)/E переменный, так как свя­зан с 0ц нелинейно (§1.3). Однако при малых деформациях 8<<1 напряжение^«(dc/ds), и из (1.3.8) (dx/dy) * sin²Xo(l-sin²\o) (da/de), что в наилучшей для одинарного скольжения ориентировке (хо = А._о = 45⁰) при модуле Юнга Е - 2(7(1+v) * 8G/3 дает 0'и «(²/з)0ц (задача 29). В грубых оценках 0'ц И 0и часто взаимозаменяемы.

Мало важен и учет анизотропии модуля упругости G, в кубических решетках изме­ряемой (§2.1) отношением упругих постоянных qG = {с\\ -с\2)/2саа- В ряду Al, Ni, Pd, Au, Ag, Cu, Pb оно убывает от 0,81 до 0,26 (по сравнению с qG - 1 в изотропной среде). Мо­дуль упрочнения D нормируют [63] либо на модуль G\ - (сц -сп + с^УЗ, связывающий деформации и напряжения в системе [110]{111}, либо на G2-[c^{c\\-c\2)]^ml2, описы­вающий взаимодействие параллельных винтовых дислокаций [110]. Различие G\ и Gi при этих qG не превышает 3 %.

Симметричные ориентировки. Симметричная исходная ориентиров­ка монокристалла включает сразу две или более равноправных систе­мы скольжения. Вместо легкого скольжения начинается сразу стадия II (или III). Хотя длинных линий первичного скольжения нет, ячеистая структура та же, и диаграммы деформации на II стадии обычно разли­чаются мало.

При растяжении алюминия вдоль оси симметрии [111] уже при деформации 2% в равной мере работают системы скольжения с тремя разными b и структура ячеистая [44]. При растяжении меди вдоль [112] слои дислокаций в линиях скольжения образуют сетку ромбов (с углом 67...76° при ожидаемом 70,5°) [60], а когда одинаково нагружены 8 систем скольжения, слои дислокаций в плоскостях (110) и (ijo) разбивают объем на

квадратные ячейки - "палочки” вдоль оси растяжения [001], и диаграмма деформации с самого начала параболическая, но с очень крутым начальным упрочнением (при 295 К 0 * Vno). Если ось растяжения отклонить на 8° от [001], скольжение "обычное" (в 1...2 системах).

Симметричные ориентировки оси растяжения на стороне [100] - [111] стереографиче­ского треугольника (см. рис. 9, б) устойчивые: если скольжение пойдет только в одной системе, то напряжение в ней упадет, а в конкурирующих увеличится. Вследствие этого равные деформации в обеих системах самоустанавливаются. Ориентировки на линии [100]-[110] неустойчивы: скольжение в одной системе увеличивает напряжение в ней же (задача 31). Тогда кристалл может разбиться на области с одной преобладающей систе­мой скольжения, вращающиеся при сдвиге навстречу друг другу [56]. При отклонении оси растяжения от [001] на 2° образец рассекают макрополосы одинарного скольжения, при 4...6° он разбит по длине на участки с разным сдвигом [64]. С перемещением исход­ной ориентировки от [110] к [100] модуль упрочнения меди 0ц растет в 1,8 раза [56], но при всех ориентировках он на порядок отличается от упрочнения на первой стадии.

Динамический возврат. По изложенной схеме стадия II должна про­должаться до сколь угодно высоких напряжений (до общей потери 42 устойчивости течения образца (§1.6) при s = d?/d<p или s/E ~ 0'_п - 10^-2). Это заложено в исходном допущении: все дислокации, участвовавшие в деформации, вносят вклад в упрочнение. Но в действительности при достаточно больших плотностях дислокаций (выше некоторого на­пряжения т_ш ) часть дислокаций теряется из-за реакций между ними (в частности, аннигиляции). Наступает III стадия - динамический возврат. Вероятность р встречи двух дислокаций разного знака пропорцио­нальна их плотностям: /?~р+р_, т. е. вероятность аннигиляции растет, а модуль упрочнения плавно уменьшается с напряжением.

Простейшее представление нелинейности - квадратичное. Для 430 диаграмм 12 ГЦК и ОЦК металлов (Белл, 1964 г.) эта III стадия - па­рабола т = (3 ^(у - у₀). Плавный переход от II стадии, где т = /)ц(у - у₂) (см. рис. 14>б), требует в точке х_ш(уз) равенства напряжений т_ш = = АКУз - Уг) и их производных dx/dy = р(у - у₀)^1/2 = Аь откуда р = (2т_шА0^1/2; ^а Уо = (У2⁺Уз)/2, И при деформациях у > у₃ модуль упроч­нения Ап монотонно убывает как An(yVAi = [(уз - Уо)(у - Уо)]¹⁷² (задача 30). Таким образом, вся диаграмма III стадии определяется одной кон­стантой - напряжением ее начала т_ш. Третьей стадии нет, если тщ на­столько высоко, что еще на II стадии образуется шейка (§1.6). При очень низком х_ш < x_s пропадает вторая стадия: параболическая диа­грамма начинается сразу за легким скольжением.

Аннигиляция лишь ослабляет накопление дислокаций в границах ячеек, не меняя основных для II стадии взаимодействий. Поэтому по следам скольжения и дислокационной структуре стадии II и III неотли­чимы: плотность дислокаций продолжает расти как р ~ т², ячейки из­мельчаются как d$ ~ х~\ а скольжение в первичной системе преоблада­ет, если ось растяжения еще не вышла на плоскость симметрии.

Когда известны предел текучести x_s, модули упрочнения 0i и 0ц и верхняя (геометрическая) граница для деформации yi (задача 21), мож­но задать и всю диаграмму, зная конец II стадии - напряжение т_ш.

Для столкновения дислокаций в одной плоскости "в лоб” надобны пробеги L ~ Г мм. На III стадии они на два порядка короче, и реакции - следствие встречи дислокаций из разных плоскостей поперечным скольжением (а при высокой температуре - и переползанием). При температуре Г->0 напряжение т_ш соответствует началу поперечного скольжения без термической активации. Если безразмерная энергия Дефекта упаковки в_ду = у_луЮЬ, то ширина расщепления дислокации сравняется с радиусом ее ядра при напряжении (задача 11) х/(7»(1/24я- -2е_ду). Если перед серией из п дислокаций напряжение лх_ш, то в ряду чистых металлов Ni, Au, Ag, Си при Г->0 измеренные [20] x/G- ~ (0,8...3,0) 10^_3 при 8_ду ~ 3 10^_3 соответствуют обычному для II стадии « ~ 10 дислокаций в серии. В сплавах х_ш растет с понижением энергии

дефекта упаковки (при Г->0 всего в полтора раза при е_ду->0, но при

высоких температурах много больше - §3.3).

При достаточно низкой энергии дефекта упаковки поперечного скольжения и пере­ползания нет. Вторая система скольжения включается после перебега, когда ось образца перевалит за плоскость симметрии и напряжение в другой системе станет выше. Ячеи­стой структуры нет - сохраняются плоские серии дислокаций, а III стадия начинается прорывом серий дислокаций второй системы через плоскости скольжения первичной с образованием собственных длинных линий скольжения (Си - 10 % (ат.) А1, е_ду = 3 10~⁴) [65]. Но модуль упрочнения 0ц тот же - он не зависит от деталей структуры.

Эффект Баушингера. От перемены схемы нагружения структура деформации обычно "рассыпается": при включении иных, бездействовавших систем скольжения сопротивле­ние течению поначалу ниже (покат не установится "собственная” структура деформации для новых систем). Это эффект Баушингера (1886 г.) - падение напряжения течения при смене растяжения сжатием и обратно. Чем устойчивее структура, тем меньше пере­стройка. Так, электронная микроскопия in situ показывает, что в меди обратная дефор­мация после 8 = 10 % сохраняет ячеистую структуру (хотя выметает дислокации из ячеек и смещает их границы), а в твердом растворе Си - 9 % (ат.) А1 (с низкой энергией дефек­та упаковки - без ячеек) распадается вся структура [66]).

Отличия ОЦК металлов. В процессах и структурах деформации есть единые (из геометрии дислокаций и подобия полей напряжений) зако­номерности, а многообразие деталей зависит от типа решетки, темпе­ратуры и скорости течения. Неизбежны (в общем случае) три стадии течения: независимое появление невзаимодействующих линий сколь­жения, упрочнение от их взаимодействия, потеря дислокаций в анниги­ляции.

Первопричины отличий деформации ОЦК металлов видны из гео­метрии решетки. Во-первых, в ОЦК не одно, а два семейства скольже­ния (24 системы), разница наибольших приведенных напряжений в них не может превышать 13 % (задача 33). Поэтому одинарное скольжение -,редкость. Во-вторых, энергия дефекта упаковки в решетке ОЦК неиз­бежно высокая (из-за его дилатации [ч.1, с. 149]) - дислокации не рас­щеплены. Но ядро винтовой дислокации <111> в состоянии покоя раз­мыто "звездой" или “крышей” в две или три плоскости, а для скольже­ния перестраивается напряжением в плоское. Поэтому по наблюдениям in situ (ниже 0,12 Тщ, в Мо и Fe и 0,09 Тпл - в Nb) подвижность винто­вых дислокаций много меньше, чем смешанных, отчего петли вытяги­ваются вдоль b и преобладают прямые винтовые дислокации [67]. Со­ответственно, вдоль b полоса скольжения в кремнистом железе длинная и прямая, а перпендикулярно b - короткая [47].

При низких температурах (0,10 Т_пл в молибдене) в начале текучести движутся крае­вые дислокации многих систем, но еще неподвижны все винтовые и потому нет размно­жения. Диаграмма скругленная, только после удлинения 6% начинается площадка одинарного скольжения с размножением [68].

Винтовую дислокацию с "неплоским” ядром одинаково трудно сдвинуть в любой из плоскостей. Оттого ее поперечное скольжение так же легко (или трудно), как и обычное. Тогда, например,^наблюдаемый in situ след движения дислокации на поверхности фоль­ги ниобия - волнистый даже без видимых препятствий [69]. Частое поперечное скольже­ние оставляет в полосе скольжения высокие ступеньки и диполи дислокаций от них, заполняющие всю полосу [70]. После растяжения железа на 20 % при 20°С ширина поло­сы до 0,2 мкм (при 800 прошедших дислокациях) [71].

Геометрия расщепления ядра в плоскостях {110} и {211} разная. Со­ответственно различаются приведенные критические напряжения т_1!0 и t₂ib ^и выбор между этими семействами уже не следует из закона Шми­да [72]. В металлах VI группы (Mo, W) и в железе ниже 0,15 Т™ сколь­жение начинается в плоскости {110}, а в щелочных - в {211} [68].

Сопротивление скольжению в плоскости {211} при расщеплении яд­ра типа b-»b/3+2b/3 или b->2b/3+b/3 разное (ч.1, с. 149). Как следствие в ОЦК металлах всех групп (Nb, Та, Mo, W, Fe и Li-Mg) находят разли­чие (иногда до 20 %) приведенных напряжений текучести i_s при растя­жении и при сжатии [68], если скольжение по плоскости (211) - но не по (110) [73].

Наконец, любые реакции между дислокациями (я/2)<111> порожда­ют только дислокации д<100>, а они неподвижны (по электронномик­роскопическим наблюдениям железа in situ [74] - до напряжений на порядок выше, чем для скольжения (all) <111>).

Все эти особенности - от типа решетки, а не от "ковалентности свя­зей" в переходных металлах; они не менее четки и в щелочных металлах (Li - 50 % Mg) [68].

Если монокристалл железа достаточно совершенный, его удается точно ориентировать для одинарного скольжения. Тогда при 300 К диаграмма растяжения такая же трехстадийная [75 , 76], как и в ГЦК металлах, примерно с теми же модулями упрочнения: 0^4 ЮЛ 9ц~ 'Uio-'hw- Чаще, однако, диаграмма параболическая - III стадия с самого начала.

В одном и том же кристалле железа при 300 и 195 К ориентировка для сдвига по (110) давала параболическую, а по (211) - трехстадийную диаграмму [77]. Так же и в других ОЦК металлах 0ц ~ /т—'Uoo, а 0_Ь например, в молибдене 3 10^ [73], и при 0,02...0,16 Тщ, есть и параболи­ческие, и трехстадийные диаграммы [24], [78]. В ориентировке для оди­нарного скольжения трехстадийную диаграмму получали у ниобия [79], ванадия [80]; 0ц = V₆oo У ниобия и тантала при 0,10...0,18 Тщ, [81].

Ячеистая структура формируется к III стадии [82] и при 0,15...0,33 Т^_л похожа на структуру в ГЦК металлах [68]. I стадию (т/С7 = 610 ;

~ ^ооо) в монокристалле Fe - 0,9 % Si после деформации yi = 0,68 (плотность дислокаций 3,5 10⁹ см^-2) сменяла III - со скачком модуля упрочнения в 5 раз. Погашение "основных” дислокаций показало, что Уже на I стадии 10 % дислокаций - вторичной системы. Но лишь когда полосы скольжения первичной системы станут для них "непрозрачны", накопив от реакций сидячие дислокации я<100>, наступает III стадия. На ней плотности дислокации обеих систем сравниваются (при 2 Ю¹⁰ см”²) [83].

Гексагональные металлы. Геометрия гексагональной решетки (§1.3) Порождает свои особенности процесса и диаграммы деформации. Плотноупакованная плоскость базиса - единственная, а сопротивление скольжению ’’рифленых” (см. рис. 7) плоскостей пирамиды и призмы сильно различается. Поэтому закон Шмида не действует. Энергии де­фекта упаковки высокие (из-за “рифления”), и дислокации почти не расщеплены: как показывает электронная микроскопия с разрешением решетки [84], в плоскости призмы а-титана ширина расщепления г/b = 3,5. Но поперечное скольжение сильно затруднено, потому что оно меняет тип плоскости скольжения: Б<->Пр; Б<->П1; Пр<->П1 (см. рис. 6) для обычного вектора Бюргерса а.

Почти все наблюдавшиеся дислокационные реакции: ai+a₂->a₃; g+a->c; gi+a-»g₂; gi+g₂-*a; gi+g₃->2a; gi+g₄-*ai+a₂ тоже меняют тип плоскости скольжения (кроме первой). В цинке ("длинная" ось с) кри­тическое напряжение пирамидального скольжения в 30...50 раз выше, чем базисного (т₈/(7~310^ и ПО^-5 соответственно), и I стадия диа­граммы деформации очень длинная: только при растяжении почти вдоль оси с (угол х < 10°) базисное скольжение сменяется пирамидаль­ным (либо двойникованием) [56]. Развитие полосы скольжения в тол­щину контролируется труднейшим семейством. Поэтому скольжение легкое и при действии двух систем в плоскости базиса (хотя модуль 0] выше) [56].

В почти плотно упакованном магнии критическое напряжение пирамидального скольжения всего на 12% выше, чем базисного. Одинаковы в обеих системах и isIG ~ 3 10“⁵, и модули упрочнения [56].

В титане ("короткая" ось с) скольжение обычно идет по плоскостям призмы. (Только выше 300 К поперечное скольжение Пр-»П1 легкое, и прямые следы скольжения сменя­ются волнистыми). Из-за "рифления" плоскости призмы перерасщепить ядро трудно. По наблюдениям in situ ниже 0,25 Т_пл размножение и текучесть начинаются после старта винтовых дислокаций - при высоком напряжении xJG - (1,2... 1,8) 10^_3, и на I стадии упрочнение довольно крутое (0i = (7...20) 10^-4 при 77 К и 300 К), а II стадия (где бц = V200.-Vim) начинается после сдвига yi~0,l, опять-таки после старта винтовых дис­локаций вторичной системы [85].

Большие деформации. При любом типе решетки можно получить трехстадийную диаграмму растяжения с одинаковыми законами уп­рочнения. Тем более похожи они на IV стадии: при деформациях у > 1 (обычно недостижимых при растяжении).

Модуль упрочнения 0 наибольший, когда все дислокации, произво­дившие сдвиг, сохраняются. Если же часть (1 - (3) из них аннигилирует, то когда 5р' дислокаций произведут сдвиг бу = Ьхбр', накопление со­ставит бр = рбр', прирост напряжения бт = aGb(bp)l2 у[р, а сдвига бу = £л:бр / р. Если тип структуры не меняется и пробег дислокаций х=к/^ при неизменном к, то бт/бу = aGfillk или 0 = ар/2 к, т. е.

0/0ц = Р по сравнению со II стадией, где р = 1, и модуль упрочнения убывает пропорционально доле накопления р.

При аннигиляции поперечным скольжением есть предельное р_к, ко­гда аннигилируют все винтовые дислокации и накапливаются лишь краевые. Без петель нет размножения, и как бы ни была петля вытяну- 46 та, в ней есть и краевой участок, который не может уничтожить винто­вая дислокация. Поэтому на III стадии диаграммы модуль упрочнения монотонно падает, пока не достигается IV стадия - опять с постоянным упрочнением 0i_V = Рквп^<<0ц (а когда наступит аннигиляция переполза­нием, то и V стадия, где Р->0 и 0 падает до нуля (см. рис. 14, в), и VI стадия: ср = Ои0 = О- стационарная ползучесть - §3.6).

На III стадии диаграмма параболическая: (у - уо) = Кх², где К = ШтщАь ¹¹ модуль упрочнения D - dx/dy = 1/2Кх убывает как 0/0ц = D/D\\ - хщ/х - обратно напряжению. Если к началу IV стадии останется доля р_к каждой петли (краевая ее часть), то 0iv = рк0и и xiv = хщ/рк- В А1, РЬ, Си при 77 К одинаково 0iv «2 КГ⁴, т. е. р_к~0,1» а хгvIG = (2...5) 10~³. На протяжении V стадии в меди и алюминии напряжение вырастало еще на 15... 18 %.

В меди IV стадия при 0,22 Т_пл наступала [86] после сдвига у = 1,5, а

• - при у = 4. Уже напряжение tiv»Z)iv, т. е. далеко за пределом устой­чивости течения при растяжениии (§1.6). Поэтому точка xrv достигается лишь при таких схемах нагружения (прокатка, волочение), где напря­жения измеряют не непосредственно в ходе деформации, а лишь после разгрузки “поточечно” (либо, как при кручении, усредняют - от нуля - по сечению, так что численное дифференцирование т(у) для определе­ния 0 мало надежно). Неясно поэтому, обособлена ли стадия IV с по­стоянным модулем упрочнения 0 или она неотделима от V (0jv = const четко видно при кручении, но 0 непрерывно падает при прокатке - более однородной деформации [87]).

Ячеистая структура становится отчетливой при истинной деформа­ции ф = 0,06...0,1, и ее эволюция почти заканчивается к ср = 0,3...0,4 - общая плотность дислокаций достигает Г 10^м см^-2, ячейки измельчают­ся [36] до 0,2 мкм, их границы утоняются до 0,05 мкм при неизменном развороте со ~ 0,1...0,2. Если ячеистая структура оставалась бы самопо- добна до любых деформаций, то напряжение приближалось бы асим­птотически [88] к некоторому пределу х* как х ~ x₀₀(l-e~^1/*^Y)- Но даль­нейшие большие деформации сильно меняют структуру при неболь­шом упрочнении. Решает не прирост плотности дислокаций, а их пере­распределение от больших деформаций сложившейся структуры.

Путь эволюции с неизбежностью следует из геометрии скольжения.

Ячеистая структура сформировалась на II стадии из полос скольже­ния. Последующая деформация поворачивает эти следы полос на угол (о ~ у, т. е. при у ~ 1 границы ячейки уже никак не связаны с определен­ной кристаллографической плоскостью, но зато вытянуты, как и вся­кая "сетка меток", вдоль оси растяжения. Плоскости скольжения с наи­большими напряжениями наклонены примерно под 45° к оси, и дисло­кации* бегут в них "поперек" длинных ячеек: пробеги л: ~ d§.

Рожденная границей полупетля дислокации раздувается в пределах ячейки и застревает в ее границах, не замыкаясь в кольцо. Серии дис­локаций не испускаются, сдвиги "размазаны" по ячейке. По обе сторо­ны границы действуют одни и те же системы скольжения, и в границу

в

б

Рис. 16. Эволюция ячеистой структуры: а - встречные полупетли дислокаций, испускаемые границами ячеек; 6 - аннигиляция винтовых дислокаций в границе попе­речным скольжением; в - накопление краевыми дислокациями разворота в границе из-за непараллельное™ их плоскостей скольжения

входят с двух сторон ветви одинаковых петель - противоположного знака (рис. 16). Если они винтовые, то могут аннигилировать, скользя в плоскости границы до встречи. Но у краевых дислокаций из разных ячеек векторы Бюргерса не совпадают по направлению (на угол раз­ворота ячеек со), так что остается Ab = |bi+b₂| = со b. Тогда сдвиг у - b/h в смежных ячейках добавляет их границе наклон Асо = A b/h - coy.

Достигнув разворота со > 1...2⁰, рыхлый слой границ ячеек сплющи­вается, превращая ячейки в резко очерченные фрагменты, сосущест­вующие с "фоном" из ячеистой структуры. Так, в монокристалле мо­либдена при 0,1 Т_пл уже после удлинения ф = 0,35 есть пары смежных границ наклона с разворотом 1...5⁰, очерчивающие фрагменты - поло­сы 0,2...0,5 мкм шириной и до 40 мкм длиной [36]. При ф = 0,67 между фрагментами преобладает наклон со ~ 1...3⁰ (и ось наклона перпендику­лярна оси растяжения). Плотность границ с со > 1° линейно нарастает от нуля при ф = 0,3 до 2 мкм"¹ при ф = 1,6. Чем больше угол со, тем чет­че вытянута граница вдоль оси растяжения (и никак не привязана к плоскости скольжения), нормали к ней рассеяны по стереографическо­му треугольнику равномерно. Уже для разворота на угол со~3° фраг­ментов размером ~ 0,2 мкм нужна плотность дислокаций 10 —2

р~со/Мф~ 1 10 см - все, что накоплено ранее. "Ненужное" анниги­лирует, дислокации "употребляются" на разворот фрагментов.

Появление границ зерна. Одиночная дислокация "продавливается" через субграницу наклона напряжением t/G<co/2ti (ч.1, с.204). Потому

вероятность захвата дислокации границей растет с углом со, и тогда, чем больше угол со, тем быстрее он растет. В результате на избранных границах разворот нарастает до полной их непроницаемости (если о = 3°, то тIG » 0,01) и далее до 10...50°, превращая их в границы зерна. У большинства остальных границ он остается малым. Так кристалл разбивается вдоль оси деформации длинными ножевыми границами наклона с большим углом. Накопление разворота на них обеспечивает совместное течение параллельных слоев, которые должны бы накло­няться от сдвига в разные стороны.

Иной путь - при низкой энергии дефекта упаковки (е_ду = 510^ в твердом растворе 5 % (ат.) А1 в меди): при ф = 0,58 (и р « 1 Ю¹⁰ см”²) вместо ячеек появляются четкие полосы с высокой плотностью дисло­каций [89].

Мезоструктура из дисклинаций. Появление в монокристалле границ зерна - резуль­тат самоорганизации течения в мезоскопическом ("среднем") масштабе 10...100 мкм: много больше характерного элемента структуры (фрагмента d$<\ мкм), но много мень­ше размеров образца. Силы самоорганизации создает сама структура. Поначалу длина границы с большим углом - всего несколько ячеек. Периметр границы есть петля дис- клинации (ч.1, с. 198) с вектором Франка со. В поле клиновой дисклинации с осью z нор­мальные напряжения (чЛ, с. 198) 099 = Е(а/2п, а на площадке х,у касательные [90]: а_ху = -&Аху1г\ где г² = х²+у²; А = G/2n(\-v). В плоскости, наклоненной около оси z на угол ц/ от плоскости границы у - 0, на краевую дислокацию действует напряжение Стпь = - (ЗАсо/4) sin4i|/ (задача 35). Оно наибольшее при \|/ = ±я/8 или vj/ = ± Зл/8.

В окрестностях дисклинации, малых по сравнению с длиной границы, эти напряже­ния т/G' — Зсо/87с( 1—v) ® to/5. Как только со > 1°, они превышают сопротивление границ фрагментов, и с этих пор определяют локализацию течения. Петля дисклинации втяги­вает дислокации из смежных фрагментов, увеличивая разворот со, и расширяется, дост­раивая границу. Это автокаталитический самоорганизующийся процесс: чем больше угол to на некоторой границе фрагмента, тем больше будет втянуто в нее дислокаций извне, тем больше и угол разворота, и диаметр границы - тем мощнее дисклинация на периметре и радиус ее действия - тем сильнее локализуется течение, достраивающее эту границу.

Поскольку угол о может меняться скачком в точке стыка фрагментов, а для движе­ния дисклинации нужен угол to ~ 1°, ножевая граница очерчена не одной, а серией петель Дисклинаций с со ~ 1° каждая, и последний разворот (от "наружной" петли) размазан в радиусе 1...15 мкм по скоплению втягиваемых дислокаций [36]. А сами ножевые границы постепенно очерчивают ленточные зерна поликристалла (еще не везде изолированные - "сообщающиеся" между собой).

Подобная “ротационно-сдвиговая” [36] пластичность с рождением и ростом границ по своему элементарному (дислокационному) механиз­му и происхождению сопротивления течению не отличается от предше­ствующих стадий. Ее отличия - в масштабах самоорганизации и эво­люции мезоструктуры. На этом уровне специфика типа решетки про­является слабо - картина аналогична для меди, молибдена, а-титана: при деформации ф~0,4 достигаются развороты со ~ 1° [36]. Большие Деформации ф > 1 усложняют иерархию структуры, но каждый новый ее этаж включает предыдущие. "Структура нижнего уровня" создана предыдущей стадией.

При ф = 1...5 фрагменты продолжают монотонно измельчаться (с 1 до 0,15 мкм при волочении железа, с 0,5 до 0,2 мкм - в меди [57]), а их форма не меняется. Это означает "перетяжку" - движение границ фраг­ментов относительно решетки, создающее деформацию Ду = со«1 (что при со - 0,01 по сравнению с у ~ 1 несущественно).

"Мгновенный" рельеф скольжения (после деформации и электроли­тической переполировки) показывает, что и при больших деформациях (например, у = 300% в меди [91]) сетка искривленных и ветвящихся линий скольжения в общем очерчивает фрагменты. Есть, таким обра­зом, самосогласование рассеянного (не оставляющего рельефа) сколь­жения в объеме фрагментов и движения винтовых дислокаций в их границах до аннигиляции. Ножевые границы в молибдене сдвигали половины рассекаемых ими фрагментов на 0,1...0,2 мкм [36] (дня чего в границе должно пройти до 10 дислокаций), но это всего лишь вторич­ный, аккомодационный "процесс удаления лишнего" - скольжение для аннигиляции: сдвиг вдоль оси растяжения сам по себе не дает удлине­ния.

От макросхемы деформации структура мезоуровня зависит сильнее, чем микрострук­тура. Так, прокатка равносильна сжатию по нормали N к листу и растяжению в направ­лении прокатки L. Если и L, и N - оси симметрии кристалла, равноправное действие многих систем скольжения даст тензорную плотность дислокаций frj = 0. Поэтому, например, прокатка N,L = (001)[ 110] монокристалла молибдена (когда все четыре b одинаково наклонены к N и попарно одинаково к L) при обжатии 95 % (<р = 3,0) не меняет его ориентировки - после полигонизации остаются лишь параллельные листу

субграницы из дислокаций а<100> (от реакций типа а/2[[ц ]+a/2[ni ] = а[001]). Так же

сохраняет ориентировку монокристалл алюминия при прокатке {120}< 112> или {112}<111>. Но при несимметричной ориентировке {123}<412> лист разбит на слои разной ориентировки [92]. При прокатке (100)[001 ] монокристалл кремнистого железа разбивался вдоль на сквозные по толщине макрополосы шириной 0,1 мм [36].

Сегодняшнее понимание процессов деформации позволяет предска­зывать порядок величины параметров диаграммы деформации и структуры в зависимости от состава сплава и внешних условий. Для большей точности трудны не расчеты элементарных актов, а адекват­ное статистическое описание структуры, в которой они происходят. Частные же "демонстрационные" модели не предсказывают главного: границ области существования эффекта. Для практической оценки и прогноза важнее обобщения следствий геометрии скольжения как при­чины образования структуры.