13. Геометрические характеристики плоских сечений: статические моменты площади , осевой,полярный и центробежный моменты инерции

Статический момент площади: S_x=∫ydF, S_y=∫xdF, S_x=y_cF, S_y=x_cF. Для сложной фигуры S_y=∑S_yi , S_x=∑S_xi .Осевые моменты инерции: J_x=∫y²dF, J_y=∫x²dF. Для прямоугольника J_x=bh³/12, J_y=hb³/12, для квадрата J_x=J_у=а⁴/12. Центробежный момент инерции: J_xy=∫xydF, если сечение симметрично хотя одной оси, J_xу=0. Центробежный момент инерции несимметричных тел будет положительным, если большая часть площади будет находиться в 1 и 3 квадранте. Полярный момент инерции: J_ρ=∫ρ²dF, ρ²=х²+у², где ρ – расстояние от центра координат до dF. J_ρ=J_x+J_y. Для круга J_ρ=πd⁴/32, J_x=πd⁴/64. Для кольца J_ρ=2J_х=π(D⁴-d⁴)/32=πD⁴(1-α⁴)/32. Моменты сопротивления: для прямоугольника W_x=J_x/у_max , где у_max – расстояние от центра тяжести сечения до границ по у. W_x=bh²/6, W_x=hb²/6, для круга W_ρ=J_ρ/ρ_max, W_ρ=πd³/16, для кольца W_ρ=πD³(1-α³)/16. Координаты центра тяжести: x_c=(x1F1+x2F2+x3F3)/(F1+F2+F3). Главные радиусы инерции: i_U=√J_U/F, i_V=√J_V/F. Моменты инерции при параллельном переносе осей координат: J_x1=J_хc+b²F, J_y1=J_uc+a²F, J_x1y1=J_хcyc+abF.

14. .Момент инерции простейших фигур. Для прямоугольников Ix=bh3/12,Iy=hb3/12,для круга Ix=Iy=Пd4/64.для треугольника Ix=bh3/36,Iy=hb3/48Осевым моментом инерции сечения относительно некоторой оси называется взятая п всей его площади сумма произведений элементарных площадок на квадраты их расстояний от этой оси, т.е. , .

15. Главные оси инерции. Главные моменты инерции. Вычисление моментов инерции сложных сечений. Оси инерции главные, три взаимно перпендикулярные оси, проведённые через какую-нибудь точку тела, обладающие тем свойством, что, если их принять за координатные оси, то центробежные моменты инерции тела относительно этих осей будут равны нулю. Если твёрдое тело, закрепленное в одной точке, приведено во вращение вокруг оси, которая в данной точке является главной Оси инерции, то тело при отсутствии внешних сил будет продолжать вращаться вокруг этой оси, как вокруг неподвижной. Понятие о главных Оси инерции играет важную роль в динамике твёрдого тела. Следовательно, главные центральные оси инерции — это такие взаимно перпендикулярные оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции обращается в нуль, а осевые моменты инерции имеют наибольшее и наименьшее значения.

16.Изгиб:осн.виды

Изгиб-такой вид деф.,при кот.в произв.поперечн.сеч.нагруж.элем.возник.2 внутр.силов.фактора.:1)поперечн.силаQ 2)изгиб.мом.M

Изгиб наз.чистым,если поперечн.сила=0

Изгиб наз.поперечн.,если плоскость действия нагрузок совпад.с одной из осей симметрии сеч.В любом другом случ.,изг.наз.косым.

Конструкц.,работ.на изг.наз.балкой.

17. Построение эпюр внутренних силовых факторов при изгибе: особенности построения.

Закон изменения внутренних усилий в поперечном сечении балки по ее длине можно выразить с помощью специальных графиков, называемых эпюрами.

Эпюрой изгибающих моментов (эпюрой M) называется график, изображающий закон изменения величин этих моментов по длине балки.

Эпюрой поперечных сил (эпюройQ) или эпюрой продольных сил (эпюрой N) называется график, изображающий изменение поперечных или продольных сил по длине балки.

Особенности:

На участках балки, на которых поперечная сила положительна, изгибающий момент возрастает (слева направо), а на участках, на которых она отрицательна – убывает.

Чем больше по абсолютной величине значение поперечной силы Q, тем круче линия, ограничивающая эпюру M.

На участке балки, на котором поперечная сила имеет постоянное значение, эпюра M ограничена прямой линией.

Если на границе соседних участков балки эпюра Q не имеет скачка, то линии, ограничивающие эпюру M на этих участках, сопрягаются без перелома, т.е имеют в точке общую касательную.

Если на границе соседних участков балки в эпюре Q имеется скачок, то линии, ограничивающие эпюру M на этих участках, сопрягаются с переломом.

Изгибающий момент достигает максимума или минимума в сечениях балки, в которых поперечная сила равна нулю; касательная к линии, ограничивающей эпюруM, в этом сечении параллельна оси эпюр.

На участках действия распределенной нагрузки поперечные силы изменяются по длине балки (если интенсивность q постоянна, то поперечные силы изменяются по линейному закону).

На участках балки, на которых распределенная нагрузка отсутствует, поперечные силы постоянны, а изгибающие моменты меняются по линейному закону.

19. Касательные напряжения уменьшаются и в наиболее удаленных от нейтральной оси точках обращаются в нуль, а а области нейтральной оси достигают наибольших значений . Кроме того, наибольшие значения касательных напряжений значительно меньше максимальных значений нормальных напряжений: так для консольного стержня прямоугольного поперечного сечения, нагруженного сосредоточенной силой на свободном конце, отношение максимальных значений этих напряжений

- формула Журавского

Qy – поперечная сила – const для любой точки поперечного сечения;

Jx – момент инерции сечения – постоянная величина для всего сечения относительно оси Х;

b– ширина сечения в рассматриваемой точке, b`const;

20. расчёт на прочность по касательным напряжениям.

Расчеты на прочность сводятся к тому, чтобы максимальные напряжения, возникающие в конструкции при внешних нагружениях не превышали допускаемых напряжений.

Три метода допускаемых напряжений:

(1)Метод допускаемых напряжений

(2)Метод предельных состояний.

3)Метод разрушающих нагрузок.

(1)Допускаемым напряжением называется наибольшее напряжение, при котором элемент конструкции будет работать длительное время без всякой опасности его разрушения. [s],[t]

s0-опасное напряжение;

n - коэффициент запаса.

-Пластичные материалы.

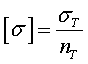
(nT=1,5-2,5)

-Хрупкие материалы.

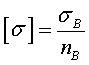
(nB=2,5-5,0)

Условие прочности:

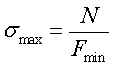
Условие прочности всегда записывается для опасного сечения.

Опасным является то сечение, в котором напряжение максимально.

(2)Предельным называется такое состояние конструкции, при котором невозможно ее дальнейшая эксплуатация.

1)gf - коэффициент надежности при нагрузке;

Pp – расчетная нагрузка (усилие);

25. Жёсткость при кручении.Угол закручивания.Проверка жёсткости.

При действии на вал крут-х моментов происх поворот 1-го сеч-ия по отн-ию к другому на нек-ый угол закручивания (фи),кот-ый опр-ся :фи=TL/GIp (рад)

Где L-длина участка вала

G-модуль упр-ти II рода

Проверка жесткости вала пров-ся по усл-ию жесткости

Фи max=TL/GIp ≤[фи

По усл-ию жесткости можно произв-ть также подбор сеч-ий GIp ≤[фи

Если подбор сеч-иё произв-ся одновр. Из усл-ий просности и жесткости,то в кач-ве расчётного принимается больший из 2-х получ-х диаметров, округлённый до ближайшей большей станд-ой величины.