42. Понятие логарифмической производной. Производная показательно-степенной функции. Производная степенной функции с любым вещесвенным показателем.

Вычислим производную функции Так как (lnx)’=1/x и (ln(-x))’=(-x)’/-x=1/x (последнее равенство получено на основании правила дифференцирования сложной функции), то производная данной функции выражаетсяследующей формулой: (1)

Учитывая формулу (1), вычислим производную сложной функции , где u=f(x) — дифференцируемая функция. Имеем или (2)

Производная называется логарифмической производной функции f(x). Для упрощения записи при логарифмическом дифференцировании знак модуля у функции f(x) обычно опускается.

С помощью логарифмической производной вычислим производную показательно-степенной функции , где u и v —некоторые функции от x(u>0), имеющие в данной точке х производные u’(x) и v’(x). Так как lny=v(x) lnu(x), то, используя формулу (2), получаем

Отсюда, учитывая, что , получаем следующую формулу для производной показательной-степенной функции:

(3)

Производная степенной функции с любым вещественным показателем. Производная функции выражается формулой .

Док-во: Так как , то lny=αlnx. По формуле (2) находим Отсюда, учитывая, что , получаем формулу для производной степенной функции: .

43. Понятие производной n-ого порядка. Формула Лейбница

О: Если производная функции Y=f(x) существует для xX, то можно говорить о существовании производной функции Y’.

О: Производная от производной I порядка функции Y=f(x) – производная II порядка Y’’=f ’’(x).

О: Производная от производной II порядка функции Y=f(x) – производная III порядка

Y’’’=f ’’’(x).

О: Производная n – го порядка функции Y=f(x) – производная от производной n –1 – го порядка Y = (f (x))’.

51. Дифференциалы высших порядков

О: Дифференциал , взятый от дифференциала dy в точке x в предположении, что x = dx – дифференциал II порядка функции Y=f(x) в точке x и обозначается d y = f ’’(x)(dx) .

О: Дифференциал n-го порядка – дифференциал , взятый от дифференциала n – 1-го порядка в предположении, что x = dx и обозначается d y=f (x)(dx) .

О: Если производная функции Y=f(x) существует для xX, то можно говорить о существовании производной функции Y’.

О: Производная от производной I порядка функции Y=f(x) – производная II порядка Y’’=f ’’(x).

О: Производная от производной II порядка функции Y=f(x) – производная III порядка

Y’’’=f ’’’(x).

О: Производная n – го порядка функции Y=f(x) – производная от производной n –1 – го порядка Y = (f (x))’.

58. Формула Тейлора

Теорема: Пусть функция f(x) имеет в точке а и некоторой ее окрестности производные порядка n+1. Пусть х —любое значение аргумента из указанной окрестности, х≠а. Тогда между точками а и х найдется точка ɛ такая, что справедлива следующая формула:

. (1)

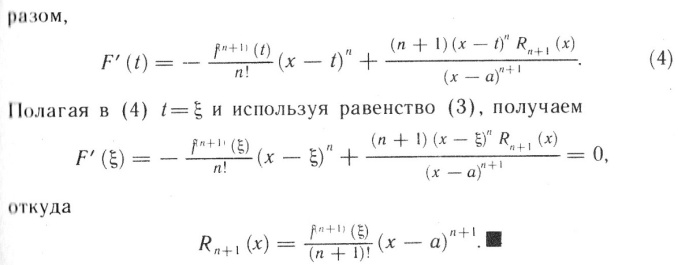
Теорема Ферма

Теорема Ферма: Если функция f(x) имеет в точке X0 локальный экстремум и дифференцируема в этой точке, то f(X0)=0.

Док-во: Пусть функция f(x) в точке X0 имеет наибольшее значение, т. е. f(x) f(X0) для х(a, b). Это значит, что Y =f(X0+X) – f(X0)  0 для  точки X0+X (a, b). Поэтому, если X>0 (т. е. x>X0), то Y/Х0 и  lim Y/Х0, т. е. f ’(X0)0, если же X<0 (т. е. x<X0), Y/Х 0и  lim Y/Х 0, т. е. f ’(X0)0. Получили, что правая производная в точке X0 неположительная, а левая – неотрицательная. По условию f ’(X0), существует и значит, f ’(X0) = f ’(X0) = f ’(X0). Это возможно только в случае, когда f ’(X0) = f ’(X0) = 0. Но тогда f ’(X0) = 0. (Для наименьшего значения аналогично)

Геометрический смысл теоремы Ферма: Если функция f(x) имеет в точке X0 локальный экстремум и дифференцируема в этой точке, т. е. существует касательная к графику функции в точке (X0; а(X0)), то эта касательная параллельна оси ОХ.

ЗАМ: теорема не верна, если функцию рассматривать на отрезке.