1.4 Расчет параметров модели двигателя и построение графиков переходных процессов при регулировании частоты вращения изменением частоты питающего напряжения

Для моделирования будем использовать модель:

Рисунок 10 – Модель асинхронный двигатель – преобразователь частоты

Проанализируем работу двигателя при изменении частоты напряжения питания обмотки статора. Для этого рассмотрим пуск при номинальной частоте и номинальном моменте и скачкообразном изменении частоты до 30 Гц.

Начальные условия:

• Напряжение питания Uс=220 В;

• Частота сети при пуске 50 Гц, через 3 секунды 30 Гц;

• Момент номинальный Мн=146,2368 Нм.

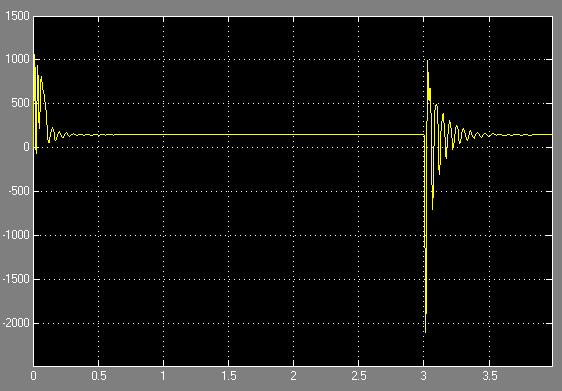
Рисунок 11 – График переходного процесса для момента

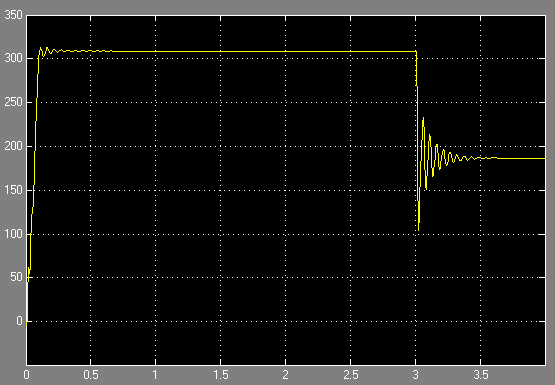
Рисунок 12 – График переходного процесса для скорости

Проанализируем полученные результаты (см. рисунки 10,11), полученные при моделировании, и сделаем выводы:

• Переходный процесс при единичном скачкообразном изменении частоты сопровождается опасными колебаниями момента. Для уменьшения и полного устранения таких пульсаций необходимо плавно снижать частоту питающей сети.

2 Системы скалярного управления

2.1 Синтез и анализ замкнутой по скорости системы скалярного управления

Таблица 6 – Исходные данные

Параметр	Значение	Ед. изм.
Номинальная частота вращения ротора	307,72	с-1
Номинальный момент Мн	146,2368	Н·м
Пусковой момент Мп	380,2158	Н·м
Номинальный ток статора Iн	81,46	А
Критическое скольжение sкр	0,15746
Активное сопротивление статора RS Приведенное активное сопротивление ротора		Ом
		Ом
Индуктивность статора LS	0,045	Гн
Приведенная индуктивность рассеяния статора и ротора		Гн
Индуктивность цепи намагничивания	0,044	Гн
Частота питающей сети fс	50	Гц
Момент инерции	0,13	кг·м2
Коэффициент магнитной связи статора и ротора kr	0,98

На рисунке 13 приведена структурная схема системы ПЧ-АД замкнутой по скорости ротора двигателя [2, c. 197].

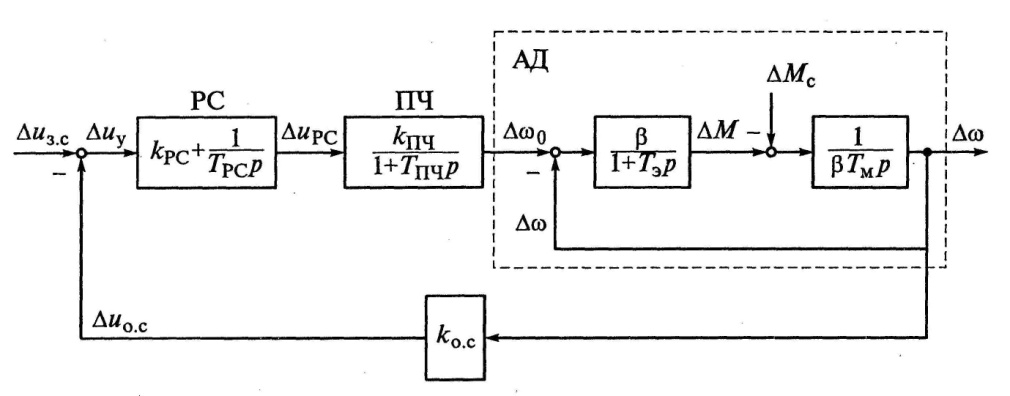
Рисунок 13 – Структурная схема системы ПЧ-АД замкнутой по скорости ротора двигателя

Расчет параметров структурной схемы [3, c. 197].

Модуль жесткости линеаризованной механической характеристики:

Эквивалентная электромагнитная постоянная времени:

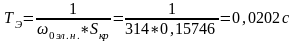
Передаточный коэффициент преобразователя частоты:

Расчет коэффициентов обратных связей

Коэффициент обратной связи по скорости:

где – максимальное напряжение задания, соответствует 10 вольтам.

Синтез передаточных функций

При синтезе передаточных функций для упрощения расчетов пренебрежем обратной связью по ЭДС двигателя. В следствии чего появится ошибка при регулировании скорости вращения ротора.

Передаточная функция разомкнутого контура регулирования скорости

где - суммарный момент инерции привода:

где - момент инерции двигателя;

- момент инерции механизма, =0,13*8=1,04

Для расчетов принимаем момент инерции механизма 8* .

Желаемая передаточная функция контура регулирования скорости настроенного на симметричный оптимум (МО):

Принимаем

В результате синтеза регулятора получим выражение для регулятора скорости:

Преобразуем выражения для реализации регулятора в модели. Для упрощения понимания структуры регулятора введем коэффициент:

Тогда регулятор скорости будет выглядеть следующим образом:

Рассчитаем данный регулятор:

Построим модель ПЧ-АД в абсолютных единицах и смоделируем пуск двигателя.

Рисунок 14 – Модель системы ПЧ-АД замкнутой по скорости ротора двигателя

В результате моделирования получили следующи1 график переходного процесса (см. рисунок 15).

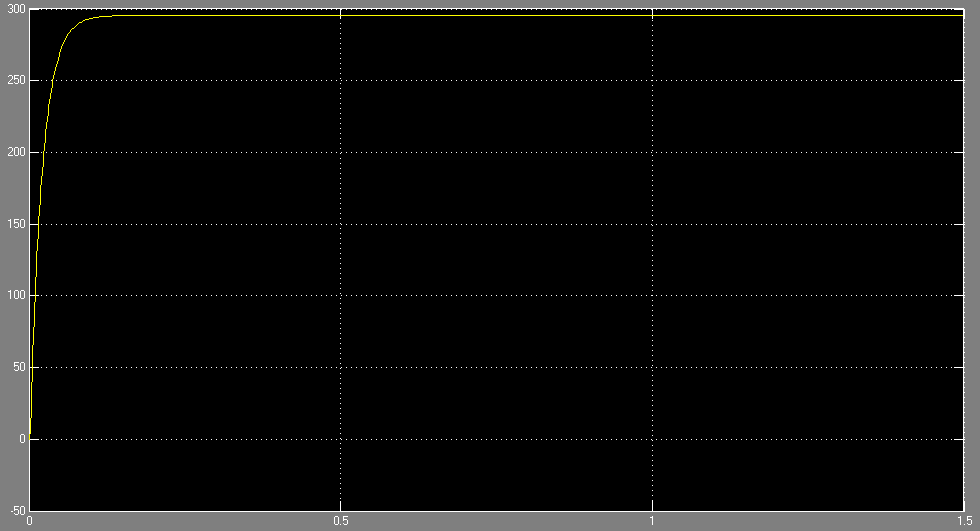
Рисунок 15 – Переходный процесс по скорости, при настройке регулятора на МО

Анализируя полученные результаты, полученные при моделировании делаем выводы:

1. Пренебрегая обратной связью по скорости внутри двигателя, мы получаем ожидаемую ошибку на валу двигателя.

2. При регулировании скорости мы не контролируем величину момента на валу двигателя, которая может достигать больших пределов.

Данная система регулирования имеет смысл лишь в том случае, если регулируется ток статора. Для чего необходимо разделить звено преобразования скорости в момент на два звена. Сигналом промежуточного звена будет ток, по которому необходимо организовать обратную связь.