Тема 7. Сравнение групп методом стьюдента
Тема: Сравнение групп методом Стьюдента
Цель: научиться выявлять достоверность различия между данными двух выборок одной и той же генеральной совокупности.
Теоретические сведения
Метод Стьюдента применяется для сравнения двух выборок, взятых из одной и той же генеральной совокупности, или двух различных состояний одной и той же выборочной совокупности.
При этом могут представиться следующие случаи:
1. По объему:
2.
а) обе группы большие (n>30);
б) обе группы малые
в) одна — большая, вторая — малая.
2. По составу:
а) группы с
попарно-зависимыми вариантами, когда
i-тая варианта первой группы сравнивается
с i-той вариантой второй группы
б) группы с попарно-независимыми вариантами (можно менять варианты местами внутри группы).
Исходя из таких условий задачи могут быть трех типов:
I. Сравнение двух больших (или одной большой, одной малой) групп с попарно-независимыми вариантами проводится по формулам:
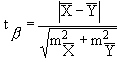(1)
(2)
где: k — число степеней свободы,
—
объем
первой выборки,
—
объем второй выборки,
— среднее арифметическое 1 группы,
— среднее арифметическое
2 группы,
— ошибка репрезентативности 1 группы,
—
ошибка репрезентативности
2 группы.
—
критерий Стьюдента,
по найденному значению которого
определяют доверительную вероятность
различия групп.
II. Сравнение двух малых групп с попарно-независимыми вариантами проводится по формулам:
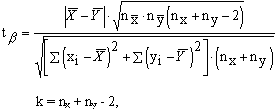(3)
где обозначения букв те же, что и в первом случае.
III. Сравнение двух малых групп с попарно-зависимыми вариантами:
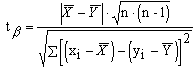(4)
или
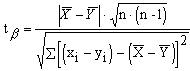(5)
Если разность
и
обозначить через
,
а разность
,
т.е
то формула (5) упростится и примет вид:
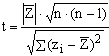
Пример 7.1.
По числу подтягиваний две группы показали следующие результаты:
=
10,0
=
35
=
±1,3
= 14,5 = 40 = ±1,5
Определить достоверность различия этих групп по средним арифметическим.
Решение:
Задача на первый случай, так как группы по объему большие и варианты попарно-независимы. Следовательно, решать нужно по формулам:
k = 35 + 40 - 2 = 73.
По таблице t-критиериев Стьюдента определим доверительную вероятность: 0,95< b <0,99. Итак, различие не случайно. Оно достоверно по I порогу доверительной вероятности.
Пример 7.2.
Результаты лыжных гонок на 15 км (в мин):
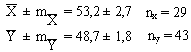
Решение:
Задача на I случай, так как одна группа большая, вторая — малая, варианты попарно-независимы. Тогда, по формулам (1) и (2) получим:
k = 29 + 43 - 2 = 70.
Вывод:
т.к.
из таблицы t-критериев Стьюдента, то
можно говорить о недостоверности
различия выборок уже по I порогу
доверительной вероятности.
Пример 7.3.
Результаты бега на коньках у мужчин на 500 м (с):
Найти оценку достоверности различия этих групп.
Решение:
Определим, на какой случай эта задача и выберем соответствующие формулы.
Задача на II случай, так как обе группы малы и варианты попарно-независимы. Следовательно, решать нужно по формулам :
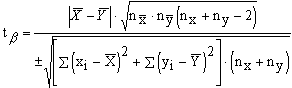
Для этого нужно
определить
из
формул:
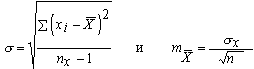
Аналогично
Тогда:
k = 25+20-2=43.
Вывод:
из
таблицы t-критериев Стьюдента, то можно
говорить о недостоверности различия
выборок уже по I порогу доверительной
вероятности.
Замечание.
Если задача на II случай, то данные выборки следует записывать в рабочую таблицу следующего вида:
Найденные суммы подставляют в соответствующие формулы:
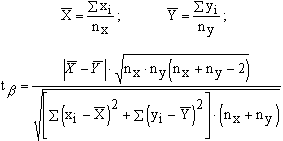
Приведенная рабочая форма применяется и в I случае, если выборки даны своими вариантами, а , , и — неизвестны.
Пример 7.4.
До начала и после подготовительного этапа тренировочного цикла в команде баскетболистов фиксировалась результативность выполнения бросков в %. Определить значимость различных состояний команды.
Решение:
Задача на третий случай, так как сравниваются два различных состояния одной и той же выборки. Решать следует по формулам (5), (6) или (5), (7).
Данные занесем в рабочую таблицу вида:
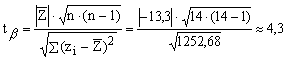
По таблице t-критериев
определим, что различие достоверно
(причем,
по II порогу доверительной вероятности.
Команда баскетболистов в результате проведенного цикла тренировок показала результаты значительно выше прежних.
Значимость определяется по формуле:
