11.2 Алгоритм построения триангуляции

Постановка задачи: Задано конечное множество точек на плоскости с вещественными координатами, . Требуется построить триангуляцию для этого множества точек.

Алгоритм решения задачи:

Будем одновременно строить выпуклую оболочку и триангуляцию (вовсе не обязательно Делоне).

Шаг 1: заводим двусвязный список в который, будем заносить отсортированные точки таким образом, чтобы можно было определить точки с совпадающими координатами по y (точки одного уровня).

Далее будем считать, что порядок в списке идет слева на право.

Шаг 2: сортируем лексикографически множество P. Берем две точки , и сравниваем координаты y. Если больше , то говорим что i-тая точка больше (i+1)-й, меняем их местами и заносим в список; если и равны, то сравниваем координаты x аналогичным образом и заносим точки в список (рис 1).

Шаг 3: Строим триангуляцию итерационно по уровням и одновременно строим выпуклую оболочку.

• Если количество точек на первом уровне больше трех, и они не лежат на одной прямой, то строим треугольник (рис 2).

• Далее идет итерация по различным координатам y (по высоте). Пусть мы имеем выпуклую оболочку на i-м шаге (для i уровней по y). Рассмотрим переход от i-го шага итерации к (i+1)-му.

1. Если i-й и (i+1)-й уровни содержат ровно по одной точке то соединяем их и переходим к шагу 4, иначе переходим к шагу 2.

2. Из точек i-го и (i+1)-го уровня берем две, первую и последнюю. Соединяем первую точку i-го уровня с первой точкой (i+1)-го уровня, и последнюю с последней этих же уровней.

3. Выберем точку p₀ из выпуклой оболочки, следующую за первой точкой i-го уровня в списке. Соединим первую точку (i+1)-го уровня с точкой p₀, получим вектор .

4. Проверим значение угла между вектором и вектором , соединяющем первые точки i-го и (i+1)-го уровней (рис 4). Для этого решим систему уравнений

Находим параметры и . Если значения и положительны, то выбираем точку p₁, следующую за p₀ и переходим к шагу 4 положив вместо p₀ p₁. Иначе, обозначаем последнюю точку, при которой и были положительными p_lt.

5. Аналогичный процесс проводим для последней точки i+1-го уровня, только идем в обратном направлении, получая точку p_rt (Рис 3).

• Строим триангуляцию для (i+1)-го уровня

1. Последовательно соединяем крайнюю левую точку (i+1)-го уровня отрезками с точками от p₀ до p_lt из выпуклой оболочки.

2. Аналогично соединяем крайнюю правую точку (i+1)-го уровня отрезками с точками от p₀ до p_rt из выпуклой оболочки.

3. Для точек лежащих на уровнях i и i+1 строим триангуляцию.

• Перестраиваем выпуклую оболочку

1. Удаляем из выпуклой оболочки ребра от точки p_lt до точки p_rt.

2. Добавляем в цепь p_rt – крайнюю правую точку и p_lt – крайнюю левую точку.

а)	б)
в)	г)

Рис. 11.4.

12. Алгоритмы геометрического поиска

12.1 Поиск в плоском случае

Для начала дадим несколько необходимых определений.

Поисковое сооб­щение, в соответствии с которым ведется просмотр файла, обычно именуется запросом. От типа файла и от набора допустимых запросов будут сильно зависеть организация первого и алго­ритмы обработки последних.

Пусть имеется набор геометрических данных и нужно узнать, обладают ли они определенным свойством (скажем, выпуклостью). В простейшем случае, когда этот вопрос возникает еди­ножды, было расточительством проводить предобработку в надежде ускорить прохождение последующих запросов. Назовем разовый запрос такого типа уникальным. Однако будут и запросы, обработка которых повторяется многократно на том же самом файле. Такие запросы назовем массовыми.

Рис. 12.1.

Рассмотрим случай уникального запроса для различных многогранников.

Рис. 12.2.

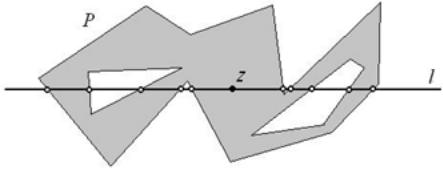
1. Дан многоугольник Р и точка z. Определим положение точки относительно многоугольника. Проведем через точку z горизонталь l (рис. 12.1.). Если l не пересекает Р, то z — внешняя точка. Поэтому пусть l пересекает Р, и рассмотрим вначале слу­чай, когда l не проходит ни через одну из вершин Р. Пусть L - число точек пересечения l с границей Р слева от z. Поскольку Р ограничен, левый конец l лежит вне Р. Будем двигаться вдоль l от -∞ направо вплоть до z. На самом левом пересечении l с границей Р мы попадем внутрь Р, на следующем пересечении выйдем наружу и т. д. Поэтому z лежит внутри тогда и только тогда, когда L нечетно. Теперь рассмотрим вырожденный случай, когда l проходит через вершины Р. Бесконечно малый поворот l вокруг z против часовой стрелки не изменит классификации (внутри/вне) точки z, но устранит вырожденность. Итак, вообразив реализацию этого бесконечно малого поворота, мы увидим: если обе вершины ребра принадлежат l, то это ребро следует отбросить; если же ровно одна вершина ребра лежит на l, то пересечение будет учтено, когда эта вершина с большой ординатой, и игнорируется в противном случае.

Рис. 12.3.

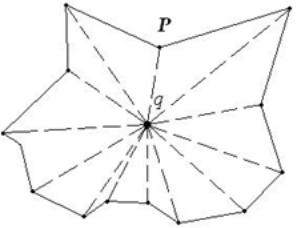
2. Исследуем нашу задачу с участием звёздного многоугольника. Предлагаемый метод использует свойство, что вершины звёздного мно­гоугольника упорядочены по полярным углам относительно некоторой внутренней точки. Такую точку q можно легко найти; звёздный многоугольник содержит по меньшей мере одну точку q такую, что отрезок qP_i лежит целиком внутри многоугольника Р для любой вершины P_i из P i = 1,…,N по определению звёздного многоугольника. Теперь рассмотрим N лучей, исходящих из точки q и проходящих через вершины многоугольника Р (рис. 12.2.).

Эти лучи разбивают плоскость на N клиньев. Каждый клин разбит на две части одним из ребер Р. Одна из этих частей лежит целиком внутри Р, другая целиком снаружи. Считая q началом полярных координат, мы можем отыскать тот клин, где лежит точка z, проведя один раз двоичный поиск, поскольку лучи следуют в порядке возрастания их углов. После нахождения клина остается только сравнить z с тем единственным ребром из Р, которое разрезает этот клин, и решить, лежит ли z внутри Р. Предобработка в вышеописанном способе решения состоит в поиске центра q, служащего основой поиска, и размещении вершин p₁, р₂, ..., p_N в структуре данных, пригодной для двоичного поиска (например, в векторе). Очевидно, это можно проделать за время 0(N) для заданной последовательности р₁, р₂, …, p_N .

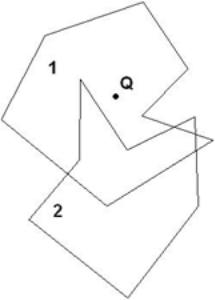
Теперь рассмотрим задачу геометрического поиска в простейшей постановке для массовых запросов с предобработкой множества многоугольников. Имеется некоторая совокупность связных не самопересекающихся многоугольников. Для заданной точки нужно определить множество многоугольников, которым она принадлежит. Считаем, что поиск ориентирован на массовые запросы (т.е., предполагается, что поиск будет осуществляться по данной совокупности тетраэдров много раз). Для эффективного решения этой задачи можно предварительно построить специальную информационную структуру-индекс и использовать ее для оптимизации поиска. Можно выделить следующие этапы построения этой структуры.

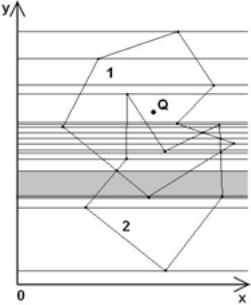
1. У нас имеется совокупность заданных многоугольников(рис. 3.). Найдем все точки пересечения сторон этих многоугольников. Проведем через эти точки и вершины многоугольников прямые, параллельные оси Х (рис. 12.4.). При этом предполагаем, что стороны многоугольников не параллельны оси Х.

2. Две такие соседние прямые образуют полосу. При этом, отрезки, которые получаются при пересечении ребер многоугольника с полосой, не пересекаются строго внутри полосы и строго внутри полосы нет вершин треугольников. Таким образом, для данной полосы мы можем упорядочить последовательность ребер многоугольника, пересекающихся с этой полосой (рис. 12.5.). Для трапеции, образуемой соседними отрезками в полосе, можно занести в структуру совокупность треугольников, в которые она входит.

Рис. 12.4.

3. Задача поиска решается в три этапа, причем, на каждом шаге используется дихотомия. Пусть дана точка (x,y), будем искать множество многоугольников, которым она принадлежит. На первом этапе ищется полоса, в которой лежит точка (x,y). На втором – трапеция в этой полосе, в которую попадает точка (x,y). Вычислительная сложность поиска равна O(ln(N)), где N-число многоугольников.

Рис. 12.5.