13. Понятие об устойчивости сжатых стержней. Формула Эйлера. Расчёт на устойчивость
Понятие об устойчивости сжатых стержней.
Потерю устойчивости прямолинейной формы равновесия центрально-сжатого прямого стержня называют продольным изгибом.
При сжимающей силе, меньшей критической, стержень работает на сжатие; при нагрузке, превышающей критическую, он подвергается совместному действию сжатия и изгиба. Даже при небольшом превышении сжимающей нагрузкой значения Fкр прогибы стержня нарастают очень быстро.
Наименьшее значение центрально приложенной сжимающей силы F, при котором прямолинейная форма равновесия стержня становится неустойчивой, называется критической силой Fкр.
Потеря устойчивости первоначальной формы упругого равновесия при достижении нагрузкой критического значения наблюдается не только для сжатых стержней, но и для ряда других элементов конструкций, например, при сжатии цилиндрической трубы.
Формула Эйлера.
Для определения наименьшего значения критической силы, при котором упругая линия изогнутого стержня характеризуется полувоной синусоиды, примем kl=π ( наименьшее значение kl, удовлетворяющее уравнению синусоиды). Тогда
Fкр=(π^2EImin)/l^2
Но для учёта характера закрепления концов стержня в формулу Эйлера вводят коэффициент приведения его длины μ.
Общее выражение критической силы при любом способе закрепления концов стержня имеет вид: Fкр=(π^2EImin)/( μl)^2
Расчёт на устойчивость
Цель расчёта на устойчивость- обеспечение работы элемента конструкции при первоначальной форме его упругого равновесия, т.е. при нагрузках , не превышающих критических.
В практических расчётах на устойчивость критическую нагрузку считают разрушающей и определяют как допускаемую: [F]= (Fкр)/[sу],
Где [sу]- требуемый( заданный) коэффициент запаса устойчивости. Обычно для стальных стержней [sу]= 1,8….3,0; для стержней из чугуна [sу]=5,0….5,5; для деревянных стержней [sу]= 2,8….3,2.
15.Балки равного сопротивления изгибу
Пусть балка имеет прямоугольное переменное сечение, для которого высота сечения h - постоянная величина, а ширина изменяется по линейному закону:
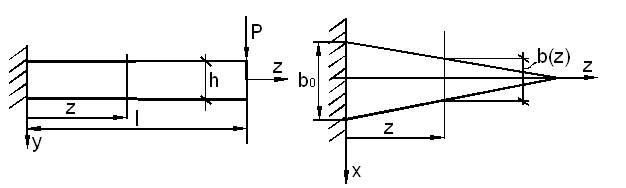
Момент инерции поперечного сечения:
Для рассматриваемой балки изгибающий момент в поперечном сечении z равен:
Согласно прогиб балки:
или с учетом :
Определим теперь максимальные напряжения по формуле:
Полагая
и
используя выражения для
и
найдем:
где
- момент сопротивления сечения в
защемлении на левом конце балки при z =
0.
Таким образом, во всех сечениях балки рассматриваемого поперечного сечения максимальные поперечные сечения максимальные напряжения получились одинаковыми. Такая балка носит название балки равного сопротивления изгибу. Изогнутая ось балки представляет собой квадратичную параболу.
16.Расчёты на прочность при кручении
Расчёт вала на прочность.
Прочность вала при кручении считается обеспеченной, если наибольшие касательные напряжения, возникающие в опасном поперечном сечении, не превышают допускаемых:
,
где τmax - максимальное касательное напряжение в брусе, определяемое по вышеприведенным уравнениям в зависимости от формы сечения; [τ] - допускаемое напряжение, назначаемое для пластичных материалов исходя из предела текучести τт. А для хрупких материалов- предела точности τв.
Экспериментально установлена зависимость между допускаемыми напряжениями при кручении [τ] и при растяжении [δ]. Для пластичных материалов обычно
[τ]=(0,5…0,65) [δ].
Для скручиваемых валов , как и для растянутых стержней, можно выполнять проверочный и проектный расчёты, определять допускаемый крутящий момент.
При проверочном расчёте находят значение τmax и сравнивают его с допускаемым напряжением:
τmax=Mk max/Wp .
При проектном расчёте определяют требуемый диаметр вала при известных значениях Mk и допускаемого напряжения [τ]. Поскольку
Wp =πd^3/32 >= Mk max/[τ],
d>= (16 Mk max/ π[τ])^1/3,
Допускаемый крутящий момент при известных [τ] и диаметре вала d определяют выражение [Mk]<= [τ] Wp.